Векторное произведение векторов. Свойства векторного произведения.
Векторным произведением векторов 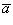 и
и 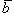 называется вектор
называется вектор 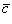 , который определяется следующими условиями:
, который определяется следующими условиями:
1) Его модуль равен 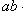
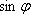 где
где 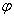 - угол между векторами
- угол между векторами 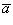 и
и 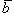 .
.
2) Вектор 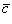 перпендикулярен к плоскости, определяемой перемножаемыми векторами
перпендикулярен к плоскости, определяемой перемножаемыми векторами 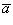 и
и 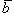 .
.
3) Вектор 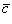 направлен так, что наблюдателю, смотрящему с его конца на перемножаемые векторы
направлен так, что наблюдателю, смотрящему с его конца на перемножаемые векторы 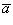 и
и 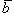 , кажется, что для кратчайшего совмещения первого сомножителя со вторым первый сомножитель нужно вращать против часовой стрелки (см. рисунок).
, кажется, что для кратчайшего совмещения первого сомножителя со вторым первый сомножитель нужно вращать против часовой стрелки (см. рисунок).
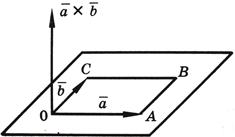
Векторное произведение векторов 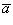 и
и 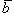 обозначается символом
обозначается символом 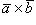 :
:
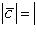
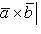
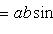
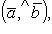 (25)
(25)
или
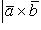
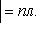
 (26)
(26)
Основные свойства векторного произведения:
1) Векторное произведение 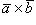 равно нулю, если векторы
равно нулю, если векторы 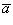 и
и 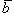 коллинеарны или какой-либо из перемножаемых векторов является нулевым.
коллинеарны или какой-либо из перемножаемых векторов является нулевым.
2) При перестановке местами векторов сомножителей векторное произведение меняет знак на противоположный (см. рисунок):
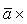
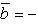
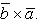
Векторное произведение не обладает свойством переместительности.
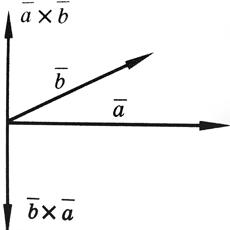
9) Площадь параллелограмма. Необходимое и достаточное условие коллинеарности двух векторов. для коллинеарности двух векторов 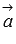 и
и 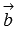 необходимо и достаточно, чтобы они были связаны равенствами
необходимо и достаточно, чтобы они были связаны равенствами 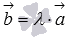 или
или 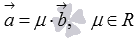 .
.
Перейдем к координатной форме полученного условия коллинеарности двух векторов.
Пусть вектор 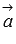 задан в прямоугольной декартовой системе координат на плоскости и имеет координаты
задан в прямоугольной декартовой системе координат на плоскости и имеет координаты 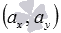 , тогда вектор
, тогда вектор 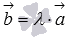 имеет координаты
имеет координаты 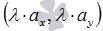 (при необходимости смотрите статью операции над векторами в координатах). Аналогично, если вектор
(при необходимости смотрите статью операции над векторами в координатах). Аналогично, если вектор 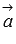 задан в прямоугольной системе координат трехмерного пространства как
задан в прямоугольной системе координат трехмерного пространства как 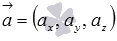 , то вектор
, то вектор 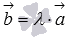 имеет координаты
имеет координаты 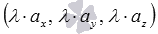 .
.
Следовательно, для коллинеарности двух ненулевых векторов 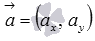 и
и 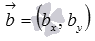 на плоскости необходимо и достаточно, чтобы их координаты были связаны соотношениями:
на плоскости необходимо и достаточно, чтобы их координаты были связаны соотношениями: 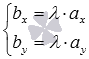 или
или 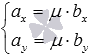 .
.
Для коллинеарности двух ненулевых векторов 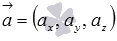 и
и 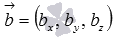 в пространстве необходимо и достаточно, чтобы
в пространстве необходимо и достаточно, чтобы 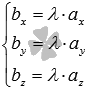 или
или 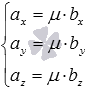 .
.
Получим еще одно условие коллинеарности двух векторов, основанное на понятии векторного произведения векторов 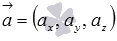 и
и 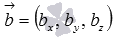 .
.
Если ненулевые векторы 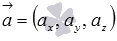 и
и 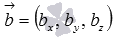 коллинеарны, то по определению векторного произведения
коллинеарны, то по определению векторного произведения 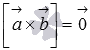 , что равносильно равенству
, что равносильно равенству 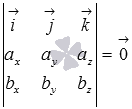 . А последнее равенство возможно лишь тогда, когда векторы
. А последнее равенство возможно лишь тогда, когда векторы 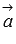 и
и 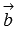 связаны соотношениями
связаны соотношениями 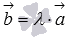 или
или 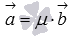 , где
, где 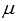 - произвольное действительное число (это следует из теоремы о ранге матрицы), что указывает на коллинеарность векторов
- произвольное действительное число (это следует из теоремы о ранге матрицы), что указывает на коллинеарность векторов 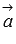 и
и 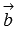 . Таким образом, два ненулевых вектора
. Таким образом, два ненулевых вектора 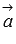 и
и 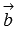 коллинеарны тогда и только тогда, когда их векторное произведение равно нулевому вектору.
коллинеарны тогда и только тогда, когда их векторное произведение равно нулевому вектору.