Двойственные задачи линейного программирования.

Пусть дана задача линейного программирования

F(x) = c₁x₁ + … + c_mx_n → max

а₁₁х₁ + а₁₂х₂ + … + с_m1х_n ≤ в₁

а₂₁х₁ + а₂₂х₂ + … + с_m2х_n ≤ в₂

....а_m1х₁ + а_m2х₂ + … + с_mnх_n ≤ в_m

Двойственной задачей является задача

Ζ (Y)= в₁у₁ + в₂у₂ + … + в_mу_m → min

а₁₁у₁ + а₁₂у₂ + … + с_m1у_n ≥ с₁

а₂₁у₁ + а₂₂у₂ + … + с_m2у_n ≥ с₂

….

а_n1у₁ + а_n2у₂ + … + с_mnу_n ≥ с_m

y_j ≥0, j = 1, 2 … m

y₁, y₂…y_m – неизвестные двойственной задачи

Неизвестных в двойственной задачи столько, сколько ограниченных неравенств в двойственной задачи. Соответствующее число ограниченной двойственной задачи равно числу неизвестной двойственной задачи. Если матрицу обозначить через (А). Если одна из пары двойственной задачи имеет оптимальное решение, то двойственная задача так же имеет оптимальное решение, причём значение целевых функций на оптимальном решении совпадают.

Если одна из задач не имеет решения, то так же не имеет решения и двойственная задача. Это утверждение позволяет сводить задачи на min, max.

Пример: Ζ (x) = 6x₁ + 7х₂ + 9x₃ → min

1х₁ + 2х₂ + 3х₃ ≥ 5

1х₁ + 1х₂ + 1х₃ ≥2

1х₁ + 2х₂ + 6х₃ ≥7

Х₁≥0; Х₂≥0; Х₃≥0

F(Y)= 5у₁ + 2у₂ + 4у₃ → max A = A^T =

 

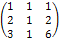
1у₁ + 2у₂ + 1у₃ ≤ 6

2у₁ + 1у₂ + … + 2у₃ ≤ 7

3у₁ + 1у₂ + 6у₃ ≤ 9

Формулы вычисления среднего выигрыша

Чтобы найти средние или математические ожидания нужно каждое значение случайной величины умножить на соответствующую вероятность и результат сложить. Значению a_ij соответствующей вероятности р_i , q_j

a_ij соответствующая вероятность р_i , q_j ; Н_А(Р,Q)

Н_А(Р,Q) = 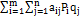(для первого)

Н_B(Р,Q) = 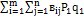(для второго)