Решение игры в смешанных стратегиях для платежной матрицы 2х2.

Если партнеры играют только 1 раз, то игрокам целесообразно придерживаться принципа минимакса в игре седловой точки, так и в игре без нее. В случае многократного повторения игры седловой точки. Когда же однократно повторяется игра без седловой точки, то постоянное использование минимакса стратегии становится не выгодным. Теорией игр доказано, что при многократно повторяемой игры без седловой точки игроку А для получения выигрыша больше, чем (альфа) следует чередовать свои стратегии,А1,А2,А3,…Аn. Подобная ситуация у игрока В.Смешанной стратегией игрока А называется применение чистых стратегий с вероятностью Р1,Р2,…Рm, причем можно записать в виде матрицы: ∑ Р_i=1 и ∑ q_i=1. S_A=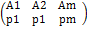S_d =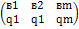Каждую чистую стратегию можно рассмотреть как частный случай, когда с частотой 1,а все другие, S_A=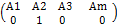Смешанные стратегии, избранные игроками, называются оптимальными, если односторонние отклоняется любым игроком от своей оптимальной может изменить средний выигрыш только в сторону не выгодным для этого игрока. Средний выигрыш В при применении игроками оптимальных значений цена игры. Стратегии входящие в стратегии с ненулевыми частотами полезные. Теорема Неймона каждая конечная игра имеет по крайней мере одно оптимальное решение вероятно в области смешанных стратегийà любая игра имеет цену ɑ≤V≤β ɑ<β общ. случай. Утверждение. Если 1 из игроков придерживается своей оптимальной стратегии, то выигрыш остается неизменным. Если 2 игрок не выходит за пределы своих полезных стратегий. Это следствие Неймона.