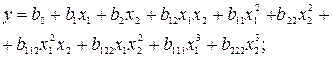Шаговый принцип
За отказ от полного перебора состояний надо чем-то платить. Цена – это предположения, которые ставятся относительно свойств неизвестной модели до начала эксперимента (априори). Некоторые из предположений никогда не могут быть проверены. Такие предположения называются постулатами. Если в действительности предположения не выполняются, то оптимум не может быть найден. Точнее, за оптимум ошибочно принимается то, что на самом деле им не является.
О свойствах поверхности отклика принимают следующие предположения. Главное – это непрерывность поверхности, её гладкость и наличие единственного оптимума (быть может, на границе области определения). Эти постулаты позволяют представить изучаемую функцию в виде степенного ряда в окрестности любой возможной точки факторного пространства (такие функции в математике называются аналитическими). Кроме того, если будет найден какой-то способ постепенного приближения к оптимальной точке, необходимо, чтобы результат не зависел от исходной точки. Если оптимум один, то неважно, приближаются к нему справа или слева, а если их несколько, да они ещё не равноценны.
На рис.4 приводятся два случая, изображающие функции отклика для одного фактора.
Рассматривая рисунки 4 а и 4 б можно заметить, что в случае «а» нет нарушений в принятых предпосылках, т.е. здесь показана гладкая непрерывная функция с одним оптимумом. На рис. 4 б много нарушений: два экстремума (оптимума) и пик (нарушение гладкости и непрерывности). Если в поисках оптимума двигаться последовательно слева направо, то найдем наименьший из максимумов и вряд ли обнаружим второй наибольший, т.к. он локализован и остер, что его несложно пропустить и при движении с правого конца, если ставить опыты не во всех точках.
Возможно, обратим внимание на то, что требование непрерывности не согласуется с представлением о дискретных уровнях факторов. Однако, в действительности это не страшно, т.к. можно считать, что фактор принимает непрерывный ряд значений (если даже некоторые значения не имеют смысла или физически нереализуемы). Важно только помнить о таком соглашении при использовании результатов. А для построения математической модели это создает значительные удобства. Если заранее считать, что предпосылки выполняются, то надо максимально использовать возможности, которые при этом открываются.
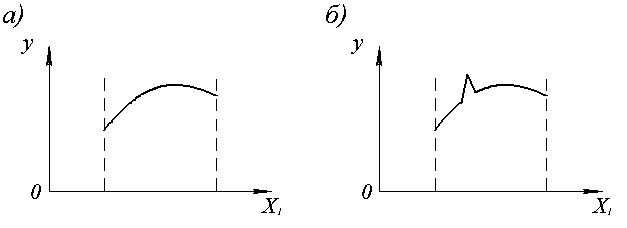
Рис.4. Примеры функций отклика для одного фактора
Если, например, известны значения параметра оптимизации в нескольких соседних точках факторного пространства, то в силу гладкости и непрерывности функции отклика можно представить результаты, которые можно ожидать в других соседних точках. Следовательно, можно найти такие точки, для которых ожидается наибольшее увеличение (или уменьшение, если требуется минимум) параметра оптимизации. Тогда ясно, что следующий эксперимент следует переносить именно в эти точки, т.е. надо продвигаться в этом направлении, пренебрегая остальными. Вот где экономятся опыты. Сделав новый эксперимент, снова можно оценить направление, в котором, скорее всего, следует двигаться. Это и есть шаговый принцип.
Для понимания шагового принципа вводятся пояснения. В факторном пространстве выбирается какая-то точка и рассматривается множество точек в её окрестности, т.е. выбирается в области определения факторов малая подобласть. Здесь предусматривается проведение эксперимента, на основании которого должна быть построена первая модель. Эта модель используется для предсказания результатов опытов в тех точках, которые не входят в эксперимент. Если эти точки лежат внутри подобласти, то такое предсказание называется интерполяцией, а если вне – экстраполяцией. Чем дальше от области эксперимента лежит точка, для которой предсказывается результат, тем с меньшей уверенностью это можно делать. Поэтому необходимо экстраполировать недалеко и использовать результаты экстраполяции для выбора условий проведения следующего эксперимента. Дальше цикл повторяется.
Полученную модель попутно можно использовать для проверки различных гипотез о механизме изучаемого явления или о его отдельных сторонах. Например, если предположить, что увеличение значения параметра некоторого фактора приводит к увеличению значения параметра оптимизации, то с помощью модели можно узнать, так ли это. Такая проверка называется интерпретацией модели.
На рис.5 изображены два варианта поиска оптимума для одной и той же поверхности. Крестиками на рисунке обозначены условия опытов. В случае «а» использован подход классический (метод Гаусса-Зейделя).
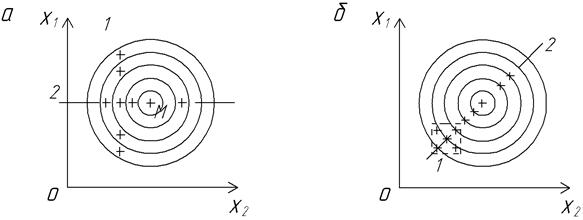
Рис. 5. Два способа поиска оптимума
Он состоит в том, что сначала последовательно изменяются значения одного фактора (на рисунке этот эксперимент обозначен 1). Затем находится и фиксируется наилучшее значение этого фактора. В этих условиях последовательно изменяются значения второго фактора (2) и т.д. (если больше факторов).
В случае «б» представлен простейший вариант шаговой процедуры. Сначала изучается локальная область (1), затем определяется наиболее интересное направление и в этом направлении ставятся следующие опыты (2).
Оказалось, что в обоих случаях достигнут одинаковый результат при одинаковом суммарном количестве опытов. Но шаговый метод (процедура «б») в среднем эффективнее, чем процедура «а». В этом можно убедиться, если представить линии равного отклика в виде эллипсов, главные оси которых составляют некоторый острый угол с осями координат. Существуют и более конкурентоспособные процедуры, чем «а», но они требуют значительно больше опытов.
Далее следует заняться выбором модели для первого эксперимента более конкретно.
3.3. Как выбрать модель?
Моделей существует много и при этом они могут быть разные. Чтобы выбрать одну из них, надо понять, что требуется от неё, т.е. необходимо сформулировать эти требования.
Главное требование к модели – это способность предсказывать направление дальнейших опытов с требуемой точностью. До получения модели неизвестно, какое направление понадобится, поэтому точность предсказания во всех возможных направлениях должна быть одинаковой. Это значит, что в некоторой подобласти, в которую входят и координаты выполненных опытов, предсказанное с помощью модели значение отклика не должно отличаться от фактического больше, чем на некоторую заранее заданную величину. Модель, которая удовлетворяет такому требованию, называется адекватной. Проверка выполнимости этого требования называется проверкой адекватности модели. Разработаны специальные статистические методы, с помощью которых проверяется адекватность модели.
Если несколько различных моделей отвечают требованиям, то необходимо выбрать самую простую. При прочих равных условиях предпочтение отдаётся степенным рядам, точнее отрезкам степенных рядов – алгебраическим полиномам. Построение полинома возможно в окрестностях любой точки факторного пространства, т.к. предполагается, что функция является аналитической. Выбрать модель – значит сравнить. А как сравнить между собой классы моделей, если свойства объекта заранее не известны? Остаётся предполагать, что должны рассматриваться такие задачи, в которых исходные постулаты окажутся верными.
Выбранные в качестве математических моделей полиномы будут различаться по максимальным степеням входящих в них переменных:
полином нулевой степени – 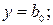
полином первой степени – 
полином второй степени – 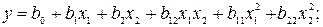
полином третьей степени –