Имитация непрерывных случайных величин

Если событие Х принимает значения в некоторой области непрерывных величин, то для аналитического моделирования непрерывных событий применяют функцию распределения вероятностей F(Х<х) или плотность распределения вероятностей f(х). Функция распределения вероятностей F(Х<х) определяет вероятность того, что событие (случайная величина) Х меньше либо равно некоторому значению х, т.е. F(Х<х)=Р{Х<х}.

Задача имитации непрерывных случайных величин, описываемых аналитическим распределением вероятностей, основана на преобразованиях равномерно распределенных случайных чисел в числа с заданным законом распределения.

3.8.1. Метод обратных функций. Пусть случайная величина Х определена функцией распределения вероятностей F(х) и плотностью распределения вероятностей f(х).

Если Р — случайная величина, равномерно распределенная на отрезке [0,1], то случайная величина Х может быть получена из решения следующего уравнения:

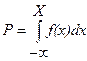. (3.29)

На рис. 3.23 приведена иллюстрация метода обратных функций. Как следует из рис. 3.23, выполняется как бы обратное преобразование вероятности Р в случайную величину Х, поэтому данный метод и получил наименование метода обратных функций.

Рис. 3.23

 

Метод обратных функций позволяет вывести правило генерирования случайной величины, имеющей произвольную функцию распределения вероятностей F(х) и плотность распределения вероятностей f(х):

- вырабатывается датчиком случайной равномерной последовательности случайное число Р;

- случайная величина (случайное число) Х, имеющая распределение f(х), находится из решения уравнения (3.29).

Пример. Пусть случайная величина Х определена функцией распределения вероятностей F(х)=1-e^-lх. Плотность распределения вероятностей f(х)= le^-lх. При известной вероятности Р значение случайной величины Х определится по формуле

.

Таким образом, получили трансцендентное уравнение Р=1‑e^-lХ с одним неизвестным Х. Решение этого уравнения:

.

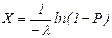В силу того, что Р — число, равномерно распределенное на отрезке [0; 1], то и 1-Р — число, равномерно распределенное на отрезке [0; 1], поэтому случайную величину Х находят по формуле

.

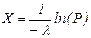На рис. 3.24 приведена схема алгоритма метода обратных функций для рассмотренного случая.

 

 

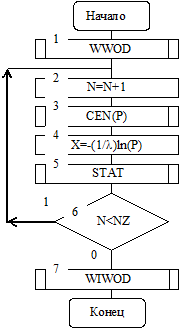
Рис. 3.24

 

Подпрограммы WWOD и WIWOD предназначены для реализации интерфейса пользователя и инициализации программного модуля. Блоками 2 и 6 организован цикл по переменной N. В подпрограмме GEN генерируется число Р, равномерно распределенное на отрезке [0; 1]. В блоке 4 определяется случайная величина Х, определенная функцией распределения вероятностей F(х)=1-e^-lх. Подпрограмма STAT предназначена для набора и обработки статистических данных о значениях случайной величины Х.

3.8.2. Метод ступенчатой аппроксимации. Метод обратных функций применим для моделирования непрерывных случайных величин Х в том случае, если существует функция распределения вероятностей F(х), т.е. уравнение (3.29) имеет аналитическое решение. Однако известны распределения случайных величин, например, нормальное распределение, для которых функция распределения вероятностей F(х) аналитически не определяется.

Для имитации случайных величин Х, определяемых только плотностью распределения вероятностей f(х), применяется метод ступенчатой аппроксимации. Рассмотрим суть этого метода. Зависимость плотности распределения f(х) представляется графически в интервале изменения случайной величины Х от a до b.

Если случайная величина задана на интервале [‑¥,+¥], то достаточно ограничиться минимально и максимально возможными числами, воспринимаемыми ЭВМ.

Суть метода ступенчатой аппроксимации показана на рис. 3.25.

Разобьем [a; b] на n интервалов таким образом, чтобы площади под кривой f(х) внутри каждого интервала были равны, как это показано на рис. 3.25, т.е.

,

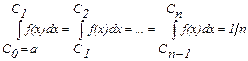где С_i() ¾ координаты точек разбиения.

Вероятность того, что случайная величина Хпопадет в любой из интервалов [С_i-1, С_i], 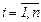, определится по формуле

,

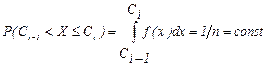т.е. попадание на любой отрезок равновероятно.

 

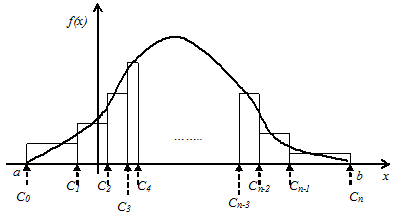
Рис. 3.25

 

Если внутри интервала распределение случайной величины Х также равномерное, то значение случайной величины Х на оси х может быть определено, как Х=С_i-1+h, где h — равномерно распределенная случайная величина на интервале [С_i-1, С_i], представляющая собой расстояние от левого конца (С_i-1) i–го интервала. На рис. 3.26 приведена схема алгоритма генерации случайных величин Х с применением метода ступенчатой аппроксимации.

Правило имитации случайных величин Х сводится к следующему:

- получаем от генератора равномерно распределенных чисел случайное число Р₁ (см. блок 3);

- из значения числа Р₁ находим индекс i=]nР₁[ интервала [С_i-1, С_i], где ]nР₁[ — целая часть числа nР₁, причем ]nР₁[<nР₁ (см. блок 4);

- получаем от генератора равномерно распределенных чисел случайное число Р₂ (см. блок 5);

- из числа Р₂ находим случайную величину h=Р₂(С_i-С_i-1), т.е. значение числа Р₂ «приводится» к величине интервала [С_i-1, С_i] (см. блок 6);

- находим случайную величину Х, имеющую заданную плотность распределения вероятностей f(х), по формуле (см. блок 7)

.

 

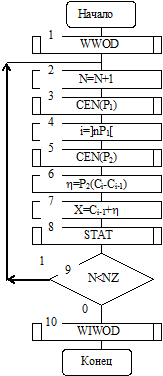
Рис. 3.26

 

Подпрограмма STAT предназначена, как и в алгоритме метода обратных функций, для набора и обработки статистических данных о значениях случайной величины Х.

3.8.3. Использование предельных теорем. Для имитации случайной величины Х, имеющей нормальный закон распределения вероятностей, используют свойство сходимости независимых величин к нормальному распределению. Для получения нормального распределения чисел с параметрами: математическое ожидание m_Х=0, среднеквадратичное отклонениеs_Х=1 удобен искусственный прием, основанный на центральной предельной теореме теории вероятностей. На рис. 3.27 приведен алгоритм получения случайный величин Х с применением свойств центральных предельных теорем.

 

 

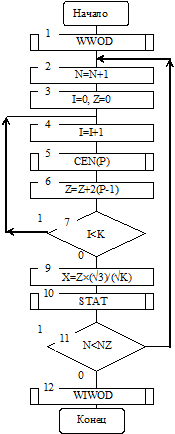
Рис. 3.27

 

Согласно центральной предельной теореме, при достаточно большом значении n величина Z может считаться нормально распределенной с параметрами

, .

Для имитации случайной величины Х в качестве исходных чисел возьмем k равномерно распределенных на отрезке [1; ‑1] случайных чисел, получаемых из интервала [0; 1] по правилу преобразования z_i=2Р_i‑1 (см. блоки 5,6). Сформируем величину Z согласно следующей формуле (см. блоки 3 – 7):

.

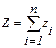Выполним нормирование величины Z и получим (см. блок 9)

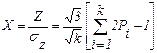. (3.30)

Случайная величина Х будет иметь нормальное распределение с m_Х=0, s_Х=1.

Установлено, что при k>8 формула (3.30) дает хорошие результаты.