Доказательство

Докажем, что для любого простого p и целого неотрицательного a, делится на p. Доказываем индукцией по a.

База. Для a=0, 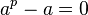и делится на p.

Переход. Пусть утверждение верно для a=k. Докажем его для a=k+1.

Но делится на p по предположению индукции. Что же касается остальных слагаемых, то 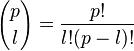. Для 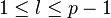, числитель этой дроби делится на p, а знаменатель — взаимно прост с p, следовательно, делится на 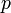. Таким образом, вся сумма 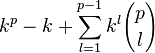делится на p.

Для отрицательных a и нечётных p теорему легко доказать подстановкой b=-a. Для отрицательных a и p=2 истинность теоремы следует из ■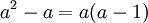

Китайская теорема об остатках/рамка

Если числа попарно взаимно просты, то для любых остатков 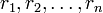таких, что 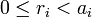при всех 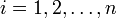, найдётся число , которое при делении на даёт остаток при всех .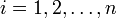

Доказательство

Применим индукцию по . При 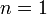утверждение теоремы очевидно. Пусть теорема справедлива при 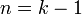, т. е. существует число , дающее остаток при делении на при . Обозначим

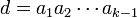
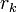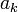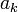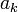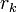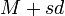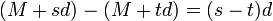и рассмотрим числа . Покажем, что хотя бы одно из этих чисел даёт остаток при делении на . Допустим это не так. Поскольку количество чисел равно , а возможных остатков при делении этих чисел на может быть не более чем (ведь ни одно число не даёт остаток ), то среди них найдутся два числа, имеющих равные остатки (принцип Дирихле). Пусть это числа и при и . Тогда их разность делится на 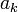, что невозможно, т. к. 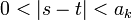и 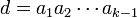взаимно просто с 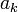, ибо числа попарно взаимно просты (по условию). Противоречие.

Таким образом, среди рассматриваемых чисел найдётся число , которое при делении на 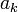даёт остаток 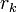. В то же время при делении на число даёт остатки 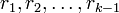соответственно. Теорема доказана.

 

Число а называется вычетом числа b по модулю m, если разность а — b делится на m (a, b, m > 0 — целые числа). Например, число 24 есть В. числа 3 по модулю 7, так как 24—3 делится на 7 4=9mod(5)

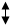
a-b=m

9-4=5

 

9) Группы, примеры групп. Подгруппы, нормальные подгруппы, факторгруппы. Теорема о гомоморфизме

 

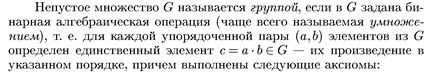
Нормальная подгруппа . H есть нормальная подгруппа G, если для любого элемента g в G gH = Hg, то есть правые и левые классы смежности H в G совпадают. Иначе говоря, если .

 

Пусть — группа, и — её нормальная подгруппа , то есть для любого элемента 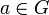его правый и левый классы смежности совпадают:

Тогда на классах смежности в можно ввести умножение:

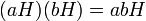
Легко проверить что это умножение не зависит от выбора элементов в классах смежности, то есть если и то 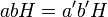. Оно определяет структуру группы на множестве классов смежности, а полученная группа называется факторгруппой по .

Факторгруппа обозначается .