рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Образование
- /
- Определение 1.
Реферат Курсовая Конспект
Определение 1.
Определение 1. - раздел Образование, ОТВЕТЫ НА БИЛЕТЫ К КОЛЛОКВИУМУ ПО ВМ-2 (2-Й СЕМЕСТР). Пусть Выполнено: 1)...
Пусть выполнено:
1)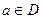 ,
, 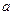 -внутренняя точка
-внутренняя точка
2) 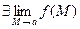
3) 
Тогда функция  называется непрерывной в точке
называется непрерывной в точке 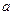
Определение 2:(непрерывность на языке  )
)
1)Пусть  .
.  =
=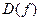 .
. 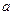 - внутренняя точка множества
- внутренняя точка множества (точка сгущения)
(точка сгущения)


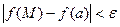 .Тогда функция
.Тогда функция  называется непрерывной в точке
называется непрерывной в точке 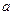
Определение 3: (непрерывность на языке последовательностей)
1) Пусть точка 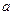
 - точка сгущения множества
- точка сгущения множества  .
.
2) Пусть  выполнено
выполнено  .
.
Тогда функция  называется непрерывной в точке
называется непрерывной в точке 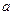
Определение 4: (непрерывность на языке приращений)
Пусть 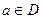 ,
, 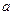 - внутренняя точка множества
- внутренняя точка множества ,
,  ,
, . Тогда функция
. Тогда функция  называется непрерывной в точке
называется непрерывной в точке 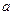
Замечание:  . Фиксируем все переменные, например
. Фиксируем все переменные, например 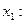
 , …,
, …,  . Тогда получим функцию одной переменной
. Тогда получим функцию одной переменной 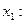
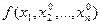 . Если окажется, что построенная функция одной переменной
. Если окажется, что построенная функция одной переменной  в точке
в точке  непрерывна, то говорят, что
непрерывна, то говорят, что  непрерывна по переменной
непрерывна по переменной 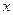 в точках
в точках 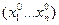 . Может оказаться, что
. Может оказаться, что  непрерывна в точках
непрерывна в точках 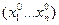 по каждой переменной в отдельности, но не является непрерывной по совокупности переменных.
по каждой переменной в отдельности, но не является непрерывной по совокупности переменных.
Пример: 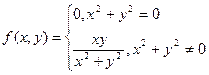
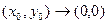 ,
,  ,
, 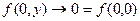
Но  не является непрерывной по совокупности переменных
не является непрерывной по совокупности переменных  .
.
БИЛЕТ 3.Частные производные ФМП. Определение, геометрический смысл.
Пусть  ,
,  ,
,  - внутренняя точка
- внутренняя точка 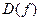
Фиксируем все переменные, кроме 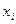 :
:  .
.

Придадим 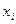 приращение
приращение  , достаточно малое, чтобы не покинуть
, достаточно малое, чтобы не покинуть 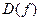
 ,
,
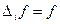
 . – частичное (частное) приращение.
. – частичное (частное) приращение.
Определение: Пусть 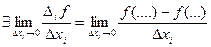 , тогда этот предел называется частной производной функции
, тогда этот предел называется частной производной функции  в точке
в точке  по переменной
по переменной 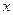 .
.
Обозначение: ,
, 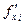
Замечание: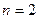 ,
, 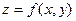 ,
, 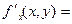

Пример:
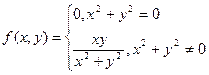
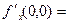
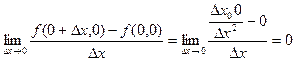
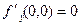
Функция  не является непрерывной в точке
не является непрерывной в точке 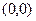 , тем не менее обе частные производные
, тем не менее обе частные производные  в точке
в точке 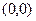 . Может быть и наоборот: функция
. Может быть и наоборот: функция  является непрерывной в точке
является непрерывной в точке 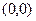 , а обе частные производные не
, а обе частные производные не в точке
в точке 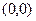 .
.
Пример:
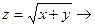 не
не частных производных в точке
частных производных в точке 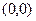 , но функция
, но функция  является непрерывной в точке
является непрерывной в точке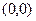
Геометрический смысл частной производной:

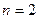 ,
, 


 ,
,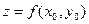
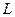 -касательная к кривой
-касательная к кривой 

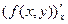
БИЛЕТ 4.Дифференцируемые ФМП. Два определения дифференцируемости. Свойства дифференцируемых функций: существование частных производных и непрерывность.
Пусть  ,
, 
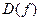 - внутренняя точка. Фиксируем
- внутренняя точка. Фиксируем  , достаточно малые, чтобы новая точка осталась внутри
, достаточно малые, чтобы новая точка осталась внутри 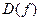 . Полное приращение функции
. Полное приращение функции  в точке
в точке  :
:  .
.
Определение: Функция  называется дифференцируемой в точке
называется дифференцируемой в точке  , если ее полное приращение в этой точке представимо в виде:
, если ее полное приращение в этой точке представимо в виде: 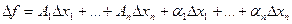 , (х)
, (х)
Где 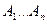 -некоторые числа, независящие от
-некоторые числа, независящие от 



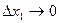
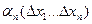 - бесконечно малые при
- бесконечно малые при 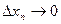
Утверждение: равенство (х) можно записать в эквивалентном виде (хх):
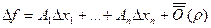 (хх), где
(хх), где 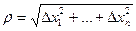 .
.
То есть (х)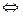 (хх)
(хх)
Утверждение: Пусть функция  дифференцируема в точке
дифференцируема в точке  . Тогда в точке
. Тогда в точке 
 частные производные по всем переменным и они равны
частные производные по всем переменным и они равны 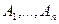 :
:
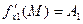 ,…,
,…,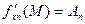 .
.
Доказательство:
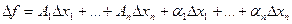 .
.
Пусть 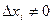 ,
,  =0
=0
 ,
, 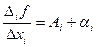 . Пусть
. Пусть 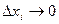 и
и  предел правой части:
предел правой части:
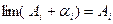 , так как
, так как  . Тогда
. Тогда  и предел левой части:
и предел левой части: 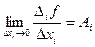
Следствие:Для дифференцируемой функции можно записать  .
.
Утверждение: Если функция  дифференцируема в точке
дифференцируема в точке  , то она непрерывна в этой точке.
, то она непрерывна в этой точке.
Доказательство:
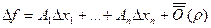 ,
, 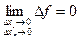 ,
, 
 непрерывна в этой точке.
непрерывна в этой точке.
БИЛЕТ 5. Теорема о достаточных условиях дифференцируемости ФМП. Полный дифференциал, частичные дифференциалы. Использование первого дифференциала в приближенных вычислениях.
Теорема (о достаточных условиях дифференцируемости):
Пусть:
1) В некоторой окрестности точки 
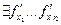
2) В самой точке 
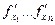 - непрерывны.
- непрерывны.
Тогда:  дифференцируема в точке
дифференцируема в точке  .
.
Доказательство:
Пусть 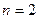
 (если же
(если же 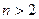 , то доказательство аналогично).
, то доказательство аналогично).
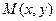


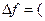
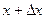 ,
,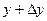 )-
)- =
=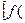
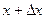 ,
,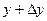 )-
)- =
=
{в [ ]- разность значений функций одной переменной, 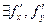 в некоторой точке
в некоторой точке 
 можно использовать формулу Лагранжа}
можно использовать формулу Лагранжа}
=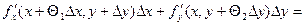 {
{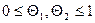 }= {
}= { - непрерывны в точке
- непрерывны в точке  }=
}= 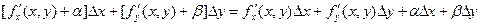
( - бесконечно малые при
- бесконечно малые при 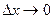
 )
) 
 дифференцируема по определению.
дифференцируема по определению.
Определение: Пусть функция  дифференцируема в точке
дифференцируема в точке  .
.
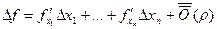 =
= 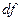 .
.
Главная линейная относительно  часть приращения функции
часть приращения функции 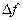 называется полным первым дифференциалом функции
называется полным первым дифференциалом функции  .
.





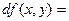

Величины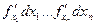 называются частичными дифференциалами
называются частичными дифференциалами 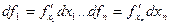
Приближенные вычисления:
Пусть функция  дифференцируема.
дифференцируема. 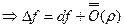

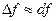 .
.
Пример:
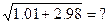
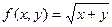
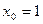

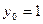

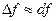 =
= =
=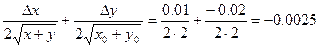
Ответ: 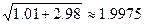
БИЛЕТ 6. Дифференцируемость сложной функции. Инвариантность формы первого дифференциала.
Пусть 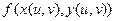 -сложная функция от переменной
-сложная функция от переменной 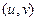 .
.
Теорема: Пусть  ,
, 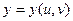 дифференцируемы в точке (
дифференцируемы в точке ( ,
, , внешняя функция
, внешняя функция  дифференцируема в точке
дифференцируема в точке  , где
, где 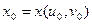 ,
,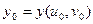 . Тогда сложная функция
. Тогда сложная функция 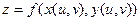 дифференцируема в точке
дифференцируема в точке 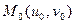 , более того
, более того
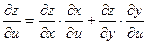 ;
;  , где производные всех функций берутся в соответственных точках.
, где производные всех функций берутся в соответственных точках.
Доказательство: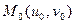 . Фиксируем
. Фиксируем  ,
,  . Тогда
. Тогда  получают точки приращения
получают точки приращения 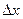 ,
,  , и изменяется значение функции
, и изменяется значение функции  .
.
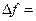 {так как
{так как дифференцируема в точке
дифференцируема в точке } =
} = 
 =
=
{так как  ,
, 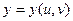 дифференцируемы в точке (
дифференцируемы в точке ( ,
, } =
} = 
+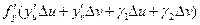 +
+
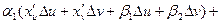
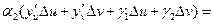
 , где
, где 
(так как  -дифференцируемая ф-я
-дифференцируемая ф-я непрерывная).
непрерывная).
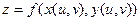 дифференцируема в точке
дифференцируема в точке 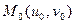 , причем ее производные по
, причем ее производные по 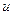 ,
,  вычисляются по формулам:
вычисляются по формулам:
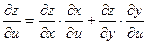 ;
;  .
.
Замечание: 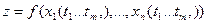 .
. 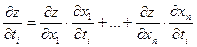 ;
; 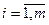
Теорема (об инвариантности формы первого дифференциала):
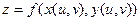
 ;
;
 .
.

 +
+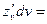
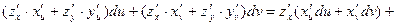
+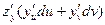 =
=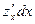 +
+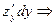 форма первого дифференциала не зависит от того, являются ли переменные в свою очередь функциями или нет.
форма первого дифференциала не зависит от того, являются ли переменные в свою очередь функциями или нет.
Следствие:Пусть 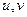 -функции. Тогда:
-функции. Тогда:

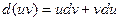
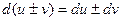
БИЛЕТ 7.Производные высших порядков. Теорема о равенстве смешанных производных.
Пусть  , также вычислена
, также вычислена  - тоже функция от переменных
- тоже функция от переменных 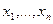 .
.
Возьмем от 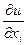 производную по переменной
производную по переменной  :
: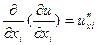 =
=
Таким образом, можно определить производные и 3-го порядка.
Замечание:  - несмешанная производная 4-го порядка. Если же среди переменных, по которым берутся производные, есть хотя бы 2 различные, то такая производная называется смешанной.
- несмешанная производная 4-го порядка. Если же среди переменных, по которым берутся производные, есть хотя бы 2 различные, то такая производная называется смешанной.
Пример:  .
.  - несмешанные производные.
- несмешанные производные.  - смешанные производные.
- смешанные производные.
Теорема(о равенстве смешанных производных):
Есть функция 
Пусть:
1) в некоторой окрестности точки 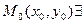 частные производные
частные производные  .
.
2) 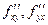 непрерывны в точке
непрерывны в точке 
Тогда 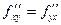 в точке
в точке  .
.
Доказательство:
Рассмотрим вспомогательное выражение:
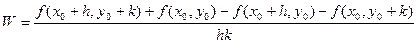 . Здесь
. Здесь  -достаточно малые чтобы оставаться в пределах окрестности из пункта 1).
-достаточно малые чтобы оставаться в пределах окрестности из пункта 1).
Вспомогательная функция:
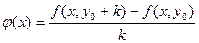 (х)
(х)
Очевидно, 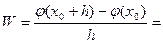
 =
=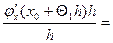
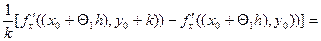
 =
=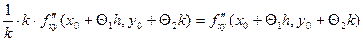 . Но
. Но 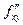 непрерывна в точке
непрерывна в точке  . Пусть
. Пусть 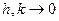 . Тогда
. Тогда 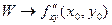 . Рассмотрим еще раз
. Рассмотрим еще раз
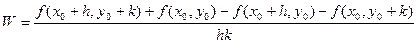 =
= , где
, где
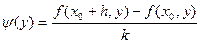 . Аналогично получаем, что при
. Аналогично получаем, что при 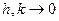
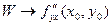 .
.
Следовательно, 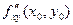
 .
.
Следствие:
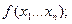
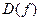 . Пусть
. Пусть  и непрерывны все частные производные до
и непрерывны все частные производные до 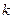 -го порядка включительно в области
-го порядка включительно в области 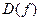 . Тогда смешанные производные до
. Тогда смешанные производные до 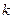 -го порядка не зависят от порядка дифференцирования.
-го порядка не зависят от порядка дифференцирования.
БИЛЕТ 8.Дифференциалы порядков выше первого. Неинвариантность дифференциалов порядка выше первого.
 .
.  . В правой части стоит функция от переменных
. В правой части стоит функция от переменных 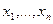 .
. 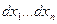 - некоторые фиксированные постоянные. Возьмем дифференциал от левой и правой частей.
- некоторые фиксированные постоянные. Возьмем дифференциал от левой и правой частей.
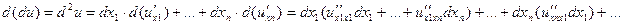
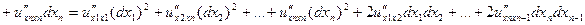 .
.
Формальная запись:
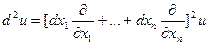 . Аналогично,
. Аналогично, 
Вообще:
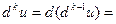

Пусть 
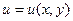
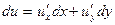

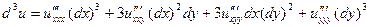 .
.
– Конец работы –
Эта тема принадлежит разделу:
ОТВЕТЫ НА БИЛЕТЫ К КОЛЛОКВИУМУ ПО ВМ-2 (2-Й СЕМЕСТР).
Функции многих переменных Основные определения Предел непрерывность определения на языке e d и на языке последовательностей Бесконечно... Частные производные функции многих переменных Определение геометрический... Дифференцируемость функции многих переменных Существование частных производных у дифференцируемой функции...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Определение 1.
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов