рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Образование
- /
- Геометрический смысл.
Реферат Курсовая Конспект
Геометрический смысл.
Геометрический смысл. - раздел Образование, ОТВЕТЫ НА БИЛЕТЫ К КОЛЛОКВИУМУ ПО ВМ-2 (2-Й СЕМЕСТР). ...
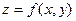 . Пусть
. Пусть  . Тогда
. Тогда 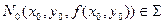 . Фиксируем
. Фиксируем 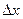 ,
, .
.
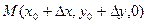 ,
, 
Пусть 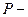 касательная плоскость к поверхности
касательная плоскость к поверхности 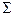 в точке
в точке 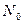 .
.

 Пусть точка
Пусть точка 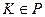 ,
, 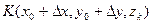 .
.
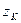 удовлетворяет уравнению
удовлетворяет уравнению 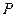

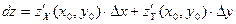
Геометрический смысл:
 геометрически равен приращению аппликаты точки
геометрически равен приращению аппликаты точки
касательной плоскости, если переменным 
приданы приращения  .
.
Если функция дифференцируема в точке  , то
, то 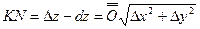 .
.
БИЛЕТ 10.Неявные функции одной переменной. Теорема о существовании неявной функции.
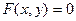
Определение:говорят, что уравнение 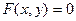 определяет однозначную неявную функцию
определяет однозначную неявную функцию 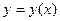 в промежутке
в промежутке 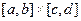 , если
, если 
 единств.
единств. 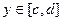 :
: 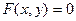
Замечание:
явное задание функции: 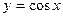 , неявное:
, неявное: 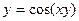 .
.
Теорема(о существовании неявной функции):
Пусть:
1)  определена и непрерывна в некоторой области:
определена и непрерывна в некоторой области:
 ,
, 
2). 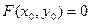
3).  является строго монотонной по
является строго монотонной по 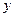

Тогда существует некоторая окрестность точки  , в которой
, в которой
а) существует однозначная функция 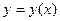
б) 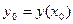
в) функция  непрерывна в этой окрестности точки
непрерывна в этой окрестности точки 
Доказательство:

 ,
, 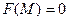
Строим 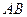 :
: . Пусть функция
. Пусть функция  монотонно возрастает
монотонно возрастает
при фиксированном 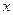 для определенности. В частности,
для определенности. В частности,
при 
1) 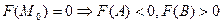
2)  непрерывна
непрерывна 

 -окрестность точки
-окрестность точки  :
:
 ,
, 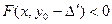 .
.
Рассмотрим произвольное значение 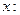
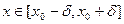 . Строим вертикальный отрезок
. Строим вертикальный отрезок 
 ,
, 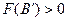 .
.
Рассмотрим  ,
,  непрерывна, имеет на концах отрезка различные знаки
непрерывна, имеет на концах отрезка различные знаки
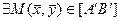 ,
, 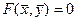
Аналогично 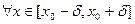 найдем и причем единственное соответствующее значение
найдем и причем единственное соответствующее значение
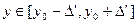 . Построена однозначная функция
. Построена однозначная функция 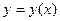 ,
, 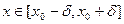 . Докажем непрерывность
. Докажем непрерывность  .
.
Фиксируем  . Необходимо доказать, что
. Необходимо доказать, что 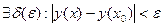 , лишь только
, лишь только  . Рассмотрим
. Рассмотрим  . Строим с центром в этой точке прямоугольник
. Строим с центром в этой точке прямоугольник
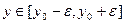 ,
,  . Аналогично проделанному выше найдем
. Аналогично проделанному выше найдем  , при
, при  .
.
Существует однозначная функция  :
: 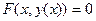 . В силу самого построения
. В силу самого построения  функция
функция  непрерывна в точке
непрерывна в точке  .
.
Докажем, что  непрерывна не только в точке
непрерывна не только в точке , но и в окрестности этой точки.
, но и в окрестности этой точки.
Рассмотрим точку  . Точка
. Точка 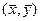 удовлетворяет всем требованиям, накладываемым в условии теоремы.
удовлетворяет всем требованиям, накладываемым в условии теоремы.
Если есть точка
 в точке
в точке  функция
функция  тоже непрерывна. (функция
тоже непрерывна. (функция  та же самая в силу однозначности)
та же самая в силу однозначности) 
 непрерывна в окрестности точки
непрерывна в окрестности точки  .
.
Замечание: Теорема утверждает, что существует некоторая малая окрестность точки  , в которой определена и непрерывна неявная функция
, в которой определена и непрерывна неявная функция  , эта окрестность может быть существенно меньше исходной.
, эта окрестность может быть существенно меньше исходной.
БИЛЕТ 11.Неявные функции одной переменной. Теорема о дифференцируемости неявной функции.
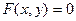
Определение:говорят, что уравнение 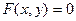 определяет однозначную неявную функцию
определяет однозначную неявную функцию 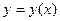 в промежутке
в промежутке 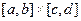 , если
, если 
 единств.
единств. 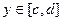 :
: 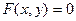
Замечание:
явное задание функции: 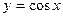 , неявное:
, неявное: 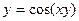 .
.
Теорема(о дифференцируемости неявной функции).
Пусть:
1)  определена и непрерывна в некоторой окрестности
определена и непрерывна в некоторой окрестности  точки
точки  .
.
 .
.
2) 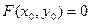
3) существуют и непрерывны 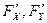 в
в  .
.
4) 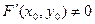 .
.
Тогда существует окрестность точки  в которой
в которой
а) существует  - однозначная неявная функция.
- однозначная неявная функция.
б) 
в)  непрерывна в этой окрестности
непрерывна в этой окрестности
г)  дифференцируема в этой окрестности, более того
дифференцируема в этой окрестности, более того 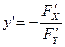 - непрерывная функция.
- непрерывная функция.
Доказательство:

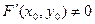 ,
, 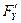 -непрерывна
-непрерывна существует некоторая окрестность точки
существует некоторая окрестность точки  , где
, где 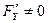 , сохраняет знак. Пусть для определенности
, сохраняет знак. Пусть для определенности  . Тогда
. Тогда  в этой новой окрестности монотонна возрастает по
в этой новой окрестности монотонна возрастает по 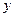 для
для  фиксированного значения
фиксированного значения 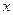
 можно применить теорему о существовании неявной функции
можно применить теорему о существовании неявной функции  в некоторой окрестности точки
в некоторой окрестности точки  уравнение
уравнение 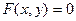 определяет однозначную неявную функцию
определяет однозначную неявную функцию  .
. 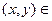 новой окрестности точки
новой окрестности точки  . Фиксируем
. Фиксируем 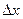
 , где
, где  .
.
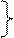
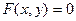


Но  имеет в
имеет в  непрерывные частные производные
непрерывные частные производные 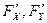
 по теореме о достаточном условии дифференцируемости, функция
по теореме о достаточном условии дифференцируемости, функция дифференцируема в
дифференцируема в 

 дифференцируема и в новой найденной окрестности точки
дифференцируема и в новой найденной окрестности точки  ,
,  , где
, где 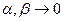 при
при 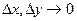 .
.
 . Пусть
. Пусть 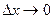 (тогда и
(тогда и  , так как
, так как  непрерывная функция
непрерывная функция 
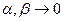 ).
).
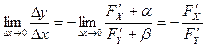 ,
, 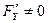
 Существует
Существует  - непрерывная функция в любой точке новой окрестности точки
- непрерывная функция в любой точке новой окрестности точки  .
.
БИЛЕТ 12. Неявные функции нескольких переменных, определяемые одним уравнением и системой уравнений. Определение, теоремы о существовании ( без доказательства )
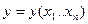 в области
в области  ,
, 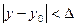 , если
, если  из данной области
из данной области 
 единственное значение
единственное значение 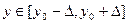 ,
,  .
.
Теорема (без доказательства):
Пусть
1)  определена и непрерывна в некоторой окрестности точки
определена и непрерывна в некоторой окрестности точки 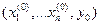
2) 
3) существуют и непрерывны все частные производные первого порядка: 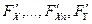 в точке
в точке
 .
.
4). 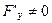 в точке
в точке 
Тогда существует окрестность точки  .
.
а) уравнение 2) определяет однозначную функцию 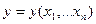
б) 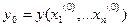
в) 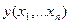 - непрерывна в этой окрестности
- непрерывна в этой окрестности
г) существуют непрерывные частные производные 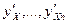 в этой окрестности.
в этой окрестности.
БИЛЕТ 12.
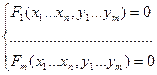 (х)
(х)
Определение: говорят, что система (х) определяет 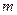 однозначных неявных функций
однозначных неявных функций 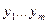 в
в 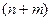 -мерном параллелепипеде.
-мерном параллелепипеде.


Если  наборе
наборе 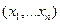 :
: 
 .
.
Определение: данная матрица называется матрицей Якоби системы функций  по переменным
по переменным 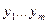 .
.
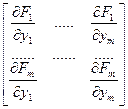 .
.
Определитель матрицы Якоби называется якобианом системы функций  по переменным
по переменным  :
:
 .
.
Теорема:
Пусть
1) в некоторой окрестности точки  функции
функции  определены и непрерывны.
определены и непрерывны.
2) 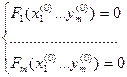
3) Существуют и непрерывны частные производные 1-го порядка по всем переменным:
 в этой окрестности.
в этой окрестности.
Тогда существует окрестность точки 
а) система уравнений (х) определяет 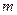 однозначных неявных функций
однозначных неявных функций 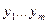
б) 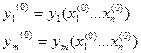
в) 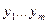 - непрерывные функции от переменных
- непрерывные функции от переменных 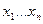
г) 
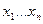 ),…,
),…,
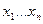 )- дифференцируемы в этой окрестности.
)- дифференцируемы в этой окрестности.
Замечание: (2)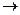 (в) сохранили в) для единообразия.
(в) сохранили в) для единообразия.
Замечание: Во всех теоремах о существовании неявных функций утверждается лишь существование малой окрестности, в которой неявная функция определена и существует. Эта окрестность может оказаться гораздо меньше исходной.
БИЛЕТ 13. Формула Тейлора для ФМП.
Пусть есть функция  . Если переменных больше, чем две, то теорема, аналогично доказанной ниже, также верна.
. Если переменных больше, чем две, то теорема, аналогично доказанной ниже, также верна.
Теорема (Тейлора). Пусть  имеет частные производные до
имеет частные производные до  -го порядка, непрерывные в некоторой окрестности точки
-го порядка, непрерывные в некоторой окрестности точки  . Тогда справедлива формула Тейлора:
. Тогда справедлива формула Тейлора:
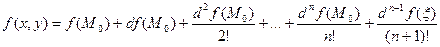 , где в
, где в 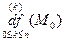 берутся в точке
берутся в точке  ,
,  ,
,  , в
, в  производные берутся в точке
производные берутся в точке 

, но  ,
,
Доказательство: Рассмотрим функцию по одной переменной
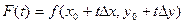 , где
, где 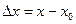 ,
,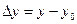 .
.
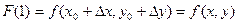
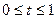

 -сложная функция, зависит от
-сложная функция, зависит от  через
через  .
.

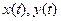 -линейные функции, для которых все дифференциалы порядка выше 1-го сохраняют свою форму.
-линейные функции, для которых все дифференциалы порядка выше 1-го сохраняют свою форму.
Функция  имеет
имеет  непрерывную производную
непрерывную производную  можно применить формулу Тейлора в окрестности точки
можно применить формулу Тейлора в окрестности точки 
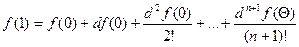 , где
, где  ,
,  .
.
Имеем: 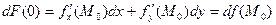 ,
, 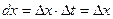 ,
, 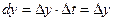
 , где
, где

……………….
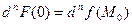
 . Таким образом,
. Таким образом,
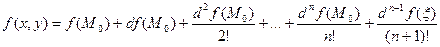 .
.
Замечание: аналогично тому, что было доказано в прошлом семестре,
 - остаточный член в формуле Лагранжа.
- остаточный член в формуле Лагранжа.
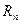 можно выписать в формуле Пьяно
можно выписать в формуле Пьяно
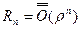 , где
, где 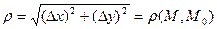
БИЛЕТ 14. Экстремум ФМП. Определение, теорема о необходимых условиях экстремума.
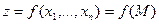
Определение: говорят, что в точке 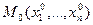 функция
функция  имеет максимум (минимум), если существует окрестность точки
имеет максимум (минимум), если существует окрестность точки  , для всех точек которой выполняется
, для всех точек которой выполняется  .
.
В случае строгого неравенства 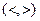 такой максимум (минимум) называется строгим. Точки максимума и минимума называются точками экстремума.
такой максимум (минимум) называется строгим. Точки максимума и минимума называются точками экстремума.
Теорема (о необходимом условии экстремума):
Пусть точка  -точка экстремума для
-точка экстремума для  . Пусть функция
. Пусть функция  имеет конечные частные производные 1-го порядка по всем переменным в точке
имеет конечные частные производные 1-го порядка по всем переменным в точке  . Тогда все частные производные 1-го порядка равны нулю в точке
. Тогда все частные производные 1-го порядка равны нулю в точке  :
: 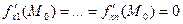 .
.
Доказательство:
 ,
,  -точка экстремума, пусть для определенности
-точка экстремума, пусть для определенности  -точка максимума. Рассмотрим функцию одной переменной
-точка максимума. Рассмотрим функцию одной переменной 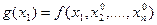 . Очевидно, что функция
. Очевидно, что функция 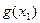 имеет максимум в точке
имеет максимум в точке 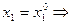 по теореме Ферма
по теореме Ферма 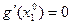 . Но
. Но 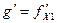
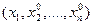

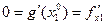
 .
.
Аналогично доказывается, что  .
.
Замечание: Необходимое условие экстремума можно записать в виде  , если
, если  -точка экстремума.
-точка экстремума.
 Замечание: Точки, в которых частные производные 1-го порядка существуют и равны нулю называются стационарными точками. Стандартные точки являются «подозрительными» на наличие экстремума.
Замечание: Точки, в которых частные производные 1-го порядка существуют и равны нулю называются стационарными точками. Стандартные точки являются «подозрительными» на наличие экстремума.
Экстремум может быть не только в стационарных точках. (Пример- конус  , для
, для
него минимум в точке 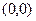
Поэтому необходимо рассматривать точки, в которых частные производные 1-го порядка не существуют или равны 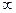 . В этих точках тоже может быть экстремум.
. В этих точках тоже может быть экстремум.
БИЛЕТ 15. Теорема о достаточных условиях наличия экстремума ФМП.
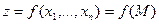
Определение: говорят, что в точке 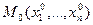 функция
функция  имеет максимум (минимум), если существует окрестность точки
имеет максимум (минимум), если существует окрестность точки  , для всех точек которой выполняется
, для всех точек которой выполняется  .
.
В случае строгого неравенства 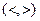 такой максимум (минимум) называется строгим. Точки максимума и минимума называются точками экстремума.
такой максимум (минимум) называется строгим. Точки максимума и минимума называются точками экстремума.
Напоминание:
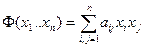 -квадратичная форма. Квадратичная форма
-квадратичная форма. Квадратичная форма 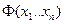 называется положительноопределенной (отрицательноопределенной), если
называется положительноопределенной (отрицательноопределенной), если 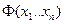
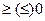 , причем
, причем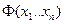

 .
.
Матрица квадратичной формы 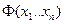 :
: 
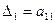 ,
, 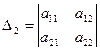 ,…,
,…,  -главные миноры.
-главные миноры.
Критерий Сильвестра:
1) Квадратичная форма 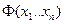 является положительноопределенной, тогда и только тогда, когда все главные миноры матрицы
является положительноопределенной, тогда и только тогда, когда все главные миноры матрицы 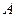 положительны.
положительны.
2) Квадратичная форма 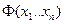 является отрицательноопределенной, тогда и только тогда, когда главные миноры матрицы
является отрицательноопределенной, тогда и только тогда, когда главные миноры матрицы 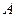 имеют чередующиеся знаки, причем
имеют чередующиеся знаки, причем  .
.
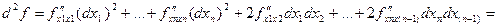 {в точке
{в точке 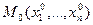 }
} (кв.форма от дифференциалов), где
(кв.форма от дифференциалов), где 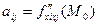 .
.
Теорема (о достаточном условии экстремума).
Пусть
1) в некоторой окрестности точки 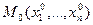 существуют и непрерывны частные производные по всем переменным до 2-го порядка включительно.
существуют и непрерывны частные производные по всем переменным до 2-го порядка включительно.
2)  - стационарная точка
- стационарная точка  , то есть
, то есть  .
.
Тогда, если квадратичная форма 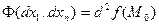 положительно (отрицательно) определена, то
положительно (отрицательно) определена, то  имеет минимум (максимум) в точке
имеет минимум (максимум) в точке  .
.
Доказательство:
Существуют непрерывные производные до 2-го порядка включительно в окрестности точки 
 можно применить формулу Тейлора. Выпишем разложение
можно применить формулу Тейлора. Выпишем разложение в окрестности точки
в окрестности точки  :
:
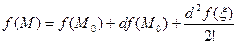
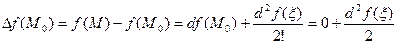 . Здесь
. Здесь  лежит на
лежит на  -мерном отрезке, соединяющем точки
-мерном отрезке, соединяющем точки  и
и 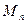 . Пусть для определенности
. Пусть для определенности 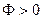 ,
,
 {так как
{так как  непрерывны в точке
непрерывны в точке  }=
}=
= ={
={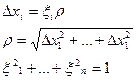 } =
} =  .
.
Получили, так как:
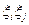 - не все равные нулю, так как
- не все равные нулю, так как 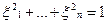
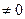
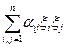
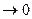 при
при 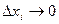 ,
, 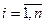
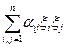 -непрерывна функция переменных
-непрерывна функция переменных 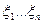 , опред.на сфере
, опред.на сфере 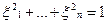 достигает точки нижней грани, которая >0, так как
достигает точки нижней грани, которая >0, так как 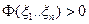
Слагаемое 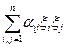
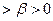 (так как граница)
(так как граница) 
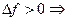 в точке
в точке  по определению минимум.
по определению минимум.
Аналогично доказывается, что если  -отрицательно определена, то в точке
-отрицательно определена, то в точке  максимум.
максимум.
БИЛЕТ 16.Теорема о достаточных условиях отсутствия экстремума ФМП. Алгоритм поиска точек экстремума.
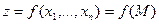
Определение: говорят, что в точке 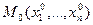 функция
функция  имеет максимум (минимум), если существует окрестность точки
имеет максимум (минимум), если существует окрестность точки  , для всех точек которой выполняется
, для всех точек которой выполняется  .
.
В случае строгого неравенства 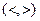 такой максимум (минимум) называется строгим. Точки максимума и минимума называются точками экстремума.
такой максимум (минимум) называется строгим. Точки максимума и минимума называются точками экстремума.
Пусть  .
.
Теорема:
Пусть:
1) В некоторой окрестности точки  существуют и непрерывны частные производные до второго порядка включительно.
существуют и непрерывны частные производные до второго порядка включительно.
2)  - стационарная точка.
- стационарная точка.
3) 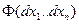 является знакопеременной квадратичной формой.
является знакопеременной квадратичной формой.
Тогда в точке  экстремум отсутствует.
экстремум отсутствует.
Доказательство:
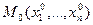 . Пусть
. Пусть  - стационарная точка (
- стационарная точка ( ). Пусть
). Пусть  .
.
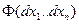 -знакопеременная квадратичная форма
-знакопеременная квадратичная форма
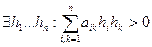 .
.

 .
.
Возьмем  . Рассмотрим
. Рассмотрим 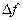 :
:  (
( ).
).
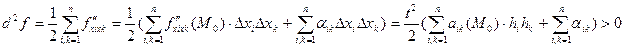 (
( - беск.м. при
- беск.м. при  ;
; при
при  ;
; 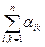
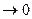 ).
).
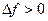 для некоторых точек
для некоторых точек  окрестности точки
окрестности точки  .
.
Аналогично показывается, что 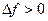 для некоторых точек, достаточно близко лежащих к
для некоторых точек, достаточно близко лежащих к  .
.

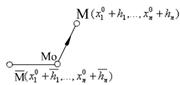
 окрестности точки
окрестности точки  присутствует некоторые точки, в которых значение функции
присутствует некоторые точки, в которых значение функции 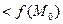

 в точке
в точке  нет экстремума.
нет экстремума.
Замечание:удобно использовать критерий Сильвестра для того, чтобы выяснить, является ли 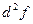 знакоопределенной.
знакоопределенной.
– Конец работы –
Эта тема принадлежит разделу:
ОТВЕТЫ НА БИЛЕТЫ К КОЛЛОКВИУМУ ПО ВМ-2 (2-Й СЕМЕСТР).
Функции многих переменных Основные определения Предел непрерывность определения на языке e d и на языке последовательностей Бесконечно... Частные производные функции многих переменных Определение геометрический... Дифференцируемость функции многих переменных Существование частных производных у дифференцируемой функции...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Геометрический смысл.
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов