Модель Эрланга

При моделировании СМО исследуется изменение в системе за сколь угодно малый отрезок времени. Составляются уравнения в частных приращениях, от которых затем осуществляется переход к дифференциальным уравнениям. Рассмотрим вывод дифференциальных уравнений, известных как модель Эрланга. Будем рассматривать одноканальную СМО с бесконечной очередью, с ожиданием, пуассоновсим потоком заявок и экспоненциальным временем обслуживания. Поток ординарный, простейший, функция распределения интервалов между заявками является экспоненциальной. Модель смены состояний можно представить в виде графа, приведенного на рис. 7.1.

 

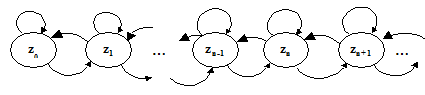
Рис. 7.1

 

Составим уравнения Эрланга в частных приращениях, которые будут отображать те изменения, которые произошли в системе за сколь угодно малое время Dt.

Из графа состояний (см. рис. 7.1) следует, что в числе состояний СМО существует «особое» состояние – состояние, при котором в СМО нет заявок. Определим это состояние, начальное состояние, когда число заявок в СМО n=0. Остальные состояния идентичны по своим связям с другими состояниями и определены числом заявок в СМО n³1. Вероятность Р₀(t+Dt) того, что СМО к моменту t+Dt останется в нулевом состоянии, определится из анализа полной группы событий:

- в момент времени t система была в нулевом состоянии и за время Dt заявки не поступали;

- в момент времени t система была в единичном состоянии (в СМО была одна заявка) и за времяDt обслуживание заявки окончилось.

Вероятность Р₀(t+Dt) определится

Р₀(t+Dt)=Р₀(t)(1-lDt)+Р₁(t)mDt,(7.1)

где 1-lDt -вероятность непоступления заявки в СМО за время Dt, mDt -вероятность окончания обслуживания заявки за время Dt.

Вероятность Р_n(t+Dt) того, что к моменту времени t+Dt система будет в n-м состоянии, определится из рассмотрения следующей полной группы событий:

- в момент времени t в системе было n-1 заявок и за время Dt поступила заявка;

- в момент времени t система была в n-м состоянии и за время Dt заявки в СМО не поступили и обслуживание не окончено;

- в момент времени t в системе была n+1 заявка и за время Dt обслуживание заявки было окончено.

Вероятность Р_n(t+Dt) определится

Р_n(t+Dt)=Р_n-1(t)lDt+Р_n(t)[1–(l+m)Dt1+Р_n+1(t)lmDt, (7.2)

где Dt -вероятность поступления заявки за время Dt; 1–(l+m)Dt -вероятность непоступления заявки в СМО и неокончания обслуживания заявки за время Dt.

Уравнения (7.1) и (7.2) представляют собой модель рассматриваемой СМО в виде уравнений Эрланга в частных приращениях. От уравнений в частных приращениях перейдем к дифференциальным уравнениям.

Для этого Р_n(t) из правой части перенесем в левую, разделим каждую часть на Dt и определим предел при Dt®0. Получим уравнения:

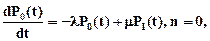
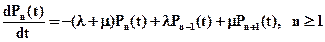(7.3)

Уравнения (7.3) представляют собой модель исследуемой СМО в виде дифференциальных уравнений Эрланга для нестационарного случая.

Так как поток заявок, поступающих в систему, отвечает условиям стационарности, то значение производных можем приравнять к нулю.

Получим модель СМО в виде уравнений Эрланга для стационарного режима

Р₁=rР₀, n=0, (1+r)Р_n=Р_n+1+rР_n-1, n³1,(7.4)

где l/m=r -коэффициент использования системы.

Решение системы уравнений (7.4) будет иметь следующий вид:

Р_n=r_nР₀, Р₀ =(1-r), Р_n = r_n (1-r),

где Р_n - вероятность того, что в СМО будет n заявок.

Затем могут быть определены такие характеристики СМО, как математическое ожидание числа заявок в СМО, математическое ожидание числа заявок в очереди и другие.