Исследование модели пуассоновского процесса с помощью производящих функций

Будем считать, что на вход СМО поступает пуассоновский поток заявок с интенсивностью l и вероятностью Р_n(t) того, что за время t в СМО поступит n заявок. Делаем предположение, что при сколь угодно малом отрезке Dt вероятность поступления заявки определится через lDt. Вероятность непоступления заявки определится как 1-lDt. Поток является ординарным.

Можно записать уравнение в частных приращениях. Вероятность того, что к моменту времени t+Dt в системе не будет заявок, определится через вероятность того, что в системе в момент времени t не было заявок, и за отрезок времени Dt заявки в систему не поступили:

Р₀(t+Dt)=Р₀(t)(1-lDt). (7.5)

Вероятность того, что к моменту времени 1+Dt в СМО будет n заявок, определится как вероятность того, что в момент t в СМО было n заявок, и за время Dt заявка не поступила, или к моменту времени t в СМО были n-1 заявок, и за время Dt поступила еще одна заявка:

Р_n(t+Dt)=Р_n(t)(1-lDt)+ Р_n-1(t) lDt. (7.6)

После проведения преобразований уравнений (7.5) и (5.6), аналогичных преобразованиям уравнений (7.1), (7.2), получим дифференциальные уравнения:

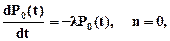
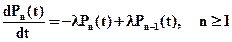. (7.7)

Рассмотрим решение уравнений (7.7) с применением производящих функций.

Производящая функция Р(z,t) для функции Р_n(t) определится

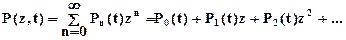
Вероятность Р_n(t) получим из производящей функции после того, как продифференцируем ее n раз и положим z=0. При решении уравнения в частных приращениях начало отсчета времени выбирается произвольно даже после того, как в систему поступило i заявок. Будем считать, что при t=0 в СМО есть i заявок. В этом случае Р_n(0)=0, если n¹iи Р_n(0)=1, если n=i. Таким образом,

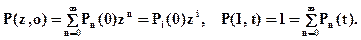
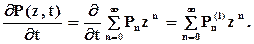
Если умножим дифференциально-разностное уравнение (7.5) на zⁿ, а дифференциально-разностное уравнение (7.6) на z⁰ и просуммируем по всем значениям n, так что

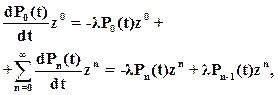
то получим, что сумма в левой части равна

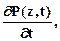
а сумма первых членов правой части равна lР(z,t). Просуммировав вторые члены правой части по n, получим

.

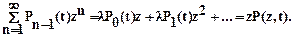Если в правой части выделить множитель lz, то всю сумму можно записать в виде lzР(z,t). Таким образом, система приводится к линейному дифференциальному уравнению для производящей функции, которое имеет вид

.

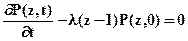Решение этого уравнения при постоянном значении z (поскольку оно не зависит от t) имеет вид

Р(z,t)=Сe^l(z-1)t.

Допустим, что к моменту t=0 не поступило ни одного требования, тогда Р(z,0)=1, так как i=0. Таким образом, С=1 и

Р(z,t)=e^l(z-1)t.

Как говорилось выше, Р_n(t) определится

.

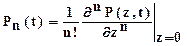Таким образом,

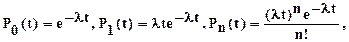
что является искомой математической моделью пуассоновского потока.

 

7.5. Модель для определения времени задержки в виде интегро-дифференциальных уравнений Линди-Такача-Севастьянова

 

Модель описывает функцию распределения времени задержки в СМО [10]. Пусть Р(w,t)- вероятность того, что заявка ожидает в очереди в течение времени w(t)£w при условии, что она поступила во время t,так что Р(w,t)=Р{w(t)£w/t}. Будем рассматривать Nà¥идентичных, одновременно действующих одноканальных СМО, на вход каждой из которых поступает пуассоновский поток заявок, а время обслуживания определяется функцией распределения В(t)=Р{b<t}, где b время обслуживания заявки.

В момент времени t все число N СМО разобъем на две группы:

- СМО, у которых время задержки w(t)£w;

- СМО, у которых время задержки w(t)>w.

Число систем первой группы равно NР(w,t), а число систем второй группы равно N-NР(w,t).

Рассмотрим изменения, которые могут произойти в момент времениt+Dt. Задача будет состоять в том, чтобы определить вероятность Р(w,t+Dt)через вероятности Р(w,t) и Р(w+ Dt,t). Для момента времени t+Dt число систем первой группы становится равным NР(w+Dt,t) минус число тех систем N_С, у которых в момент времени t было время ожидания w(t)£w, но вследствие поступления заявки за время Dt, w(t) превысит уровень w. Можно записать:

NР(w,t+Dt)=NР(w+Dt,t) - N_С.(7.8)

Поставим задачу определения числа систем N_С.

Вначале определим число систем, у которых в момент времени t w(t) находится внутри интервала (х,х+dх). Так как Р(х,t) - функция распределения вероятностей, то после дифференцирования при х>0 получим ее плотность распределения. Тогда число систем определится

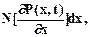еслих>0,илиNР(0,t),еслих = 0.

Предполагается, что в интервале (t,t+Dt) время ожидания превзойдет величину w, если за время Dt поступит одна заявка и если время обслуживания y этой заявки, сложенной с величиной х, превзойдет величину w, т.е. (х+y>wày>w-х). Поэтому нужно умножить число систем, у которых время ожидания равно х, на вероятность поступления одного требования за время Dt, т.е. наlDt, и на вероятность того, что время обслуживания этой заявки превзойдет величину w-х. Если b(y) - плотность распределения времени обслуживания, то вероятность последнего события равна

.

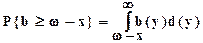Для фиксированного значения времени ожидания w>0 число систем, которые перейдут из первой группы во вторую, определится выражением

,

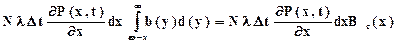которое должно быть просуммировано по всем х, х<0£w . Причем 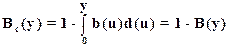. Если х=0, то число систем, переходящих во вторую группу, определится

.

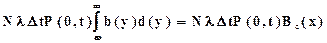Следовательно, уравнение (7.8) будет иметь вид

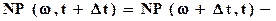
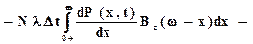
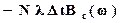. (7.9)

Применим разложение функции Р(w+Dt,t) в ряд Тейлора

,

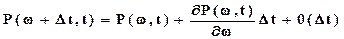разделим обе части уравнения (7.9) на N, вычтем из обеих частей Р(w,t), разделим на Dt и, перейдя к предельным выражениям, получим

.

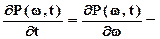
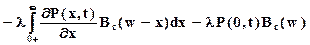Решение данного интегродифференциального уравнения должно удовлетворять условиям: Р(w,0)=1 для всех w; Р(¥,t)=1 для всех t. Интегрируем по частям:

.

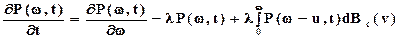Если B(t)=1-B_С(t), то

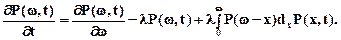(7.10)

Уравнение (7.10) носит название уравнения Линди-Такача-Севастьянова, и оно является моделью для описания времени ожидания в СМО. Для стационарного режима уравнение (7.10) примет вид

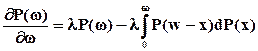. (7.11)

Математическая модель может быть представлена в виде характеристической функции, если применить к уравнениям (7.9) и (7.11) преобразование Лапласа-Стилтьеса, которое имеет вид

.

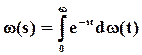Характеристическая функция распределения Р(w,t) из решения уравнения (5.9) определится

,

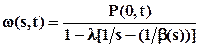где b(s) ‑характеристическая функция распределения B(t).

Характеристическая функция распределения Р(w) из решения уравнения (7.11) определится как

.
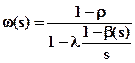