СТОХАСТИЧЕСКИЕ МОДЕЛИ ОБЪЕКТОВ

 

3.1. Математические модели случайных процессов

При проведении научных исследований в производстве и в быту часто встречаются события, которые многократно появляются при одних и тех же условиях, но отличающиеся каждый раз друг от друга. Например, измеряя значение напряжения в сети переменного тока с помощью одного и того же прибора с одинаковой тщательностью, никогда не получим одинаковых данных. Наблюдается случайное рассеивание. Для оценки величины рассеивания вводится вероятность, как мера измерения.

Закономерность рассеивания, выраженная функцией распределения вероятностей, носит общий характер.

Если входные параметры объекта, смена состояний объекта или его выходные параметры описываются случайными распределениями вероятностей, то эти объекты относятся к классу стохастических. При моделировании поведения данных объектов применяется аппарат теории вероятностей, а для идентификации параметров моделей применяется аппарат математической статистики. Рассмотрим виды моделей, которые могут быть применены для описания стохастических объектов.

3.1.1. Распределение случайных событий. Массовые явления или процессы характеризуются многократным повторением при постоянных условиях некоторых опытов (операций и прочее). Абстрагируясь от специальных свойств этих опытов, в теории вероятностей вводится понятие испытания (опыта). Испытанием называется осуществление определенного комплекса условий, который может быть воспроизведен сколь угодно большое число раз. Явления, происходящие при реализации этого комплекса условий (в результате испытания), называются событиями [8].

Положительное число в отрезке [0,1], представляющее собой количественную меру возможности реализации случайного события в испытании, называется его вероятностью. Вероятность появления события А обозначают символом Р(А), причем 0£Р(А)£1. Вероятность понимается как идеальная мера возможности появления события.

Случайная величина рассматривается как функция, аргументом которой служит элементарное случайное событие. Дискретной случайной величиной называется такая, которая может принимать конечное или бесконечное счетное множество значений, например возможны значения x₁, x₂, …, x_n, … Для каждого события x_i определены вероятности P(x_i). Распределение вероятностей дискретной случайной величины, представленное на рис. 3.1, рассматривают как точечное распределение вероятностей.

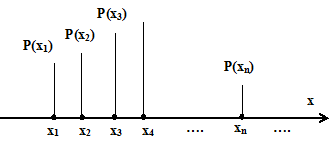
Рис. 3.1

 

При непрерывном распределении случайной величины вероятности распределены сплошной полосой по всей оси x или по некоторым ее участкам с определенной плотностью.

Распределение вероятностей носит название теоретического распределения случайной величины.

Интегральная функция распределения вероятностей определяет вероятность того, что случайная величина X меньше значения x

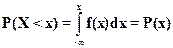. (3.1)

Пример задания интегральной функции распределения вероятностей приведен на рис. 3.2.

 

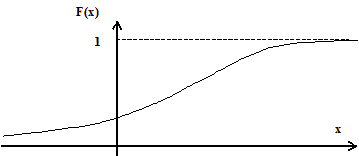
Рис. 3.2

 

Дифференциальная функция распределения вероятностей (плотность распределения вероятностей) определяет вероятность того, что случайная величина X меньше значения x

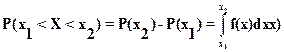. (3.2)

Пример задания дифференциальной функции распределения вероятностей приведен на рис. 3.3.

Совокупность случайных величин X(Q) аргумента Q, образует случайный процесс. Течение случайного процесса описывают некоторой функцией X(Q), где Q - аргумент функции со значениями из множества Q. Функцию X(Q), наблюдаемую в некотором опыте, соблюдая определенный комплекс условий, называют выборочной функцией или реализацией случайного процесса.

 

Рис. 3.3

 

Если множество Q произвольно, то вместо термина «случайный процесс» применяют термин «случайная функция». Название «случайный процесс» применимо в тех случаях, когда параметр Q интерпретируется как время. Если аргумент случайной функции является пространственной переменной, то функцию называют случайным полем.

Определение. Моделью случайного процесса называют случайную функцию X(Q), заданную на множестве Q, принимающую действительные значения и описываемую семейством распределений [9]:

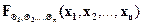, QiÎQ, i=1,2,...,n, n=1,2,...,

которое удовлетворяет условиям согласованности

,

=,

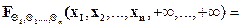
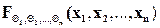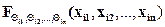где i₁, i₂,…, i_n, -любая перестановка индексов 1, 2,..., n.

Набор функций 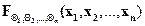называется конечномерными распределениями случайной функции или интегральной функции распределения вероятностей многомерной случайной величины. При n=1 получим одномерное распределение (3.1). Модель многомерного распределения необходима для моделирования многопараметрической случайной величины.

При решении многих задач моделирования приходится оперировать с несколькими случайными функциями. Для того чтобы над ними производить математические операции, недостаточно, чтобы каждая из этих случайных функций была задана в отдельности. Последовательность функций X₁(Q), X₂(Q),…, X_n(Q) возможно заменить векторной функцией x(Q), компонентами которой служат случайные функции X_i(Q), (i=1,2,…,n).

Явные выражения для конечномерных функций распределения случайного процесса бывают сложными и неудобными для применения. Поэтому в ряде случаев предпочитают задавать конечномерные распределения их плотностями (дифференциальной функцией распределения вероятностей многомерной случайной величины) или характеристическими функциями.

Если 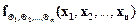- плотность функций распределения 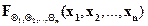, то

=

=.

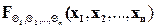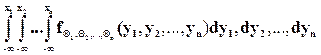Связь интегральной функции распределения вероятностей одномерной случайной величины и ее дифференциальной функцией распределения вероятностей показана формулой

.

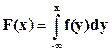Модель системы может быть задана также в виде характеристической функции конечномерного распределения последовательности

X₁(Q),X₂(Q), …, X_n(Q), Qi³0 >, i=1,n, n=1,2,...,

которая определяется формулой

,

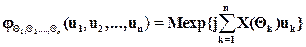где M -символ математического ожидания, u₁,u₂,...,u_k - вещественные числа.

Если существует плотность конечномерного распределения, то модель в виде характеристической функции является преобразованием Фурье плотности распределения. Для одномерной случайной величины характеристическая функция определится по формуле

.

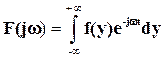3.1.2. Корреляционные функции. Исчерпывающую характеристику модели стохастического объекта в виде случайной функции в широком смысле дает семейство конечномерных распределений. Однако решение многих теоретико-вероятностных задач зависит только от небольшого числа параметров, характеризующих входящие в задачу распределения. Наиболее важными числовыми характеристиками распределений являются их моменты. В теории случайных функций роль моментов распределений играют моментные функции. Рассмотрим модели в виде моментных функций для одномерной случайной величины.

Момент k–го порядка дискретной случайной величины определяется по формуле

.

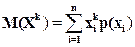Для непрерывной случайной величины моментная функция k–го порядка определяется по формуле

.

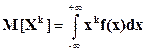Рассмотрим модели в виде моментных функций для многомерной случайной величины.

Определение. Модель случайной функции X(Q_i), Q_iÎQ в виде моментной функции задается отношением

,

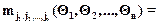
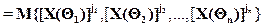если математическое ожидание в правой части равенства имеет смысл при всех QiÎQ, i=1,n. Величина q=j₁+j₂+...+j_n называется порядком моментной функции.

Если известны характеристические функции конечномерного распределения, то моментные функции с целочисленными индексами могут быть найдены с помощью дифференцирования

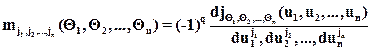
при u₁=u₁=…=u_n=0.

Кроме моментных функций в качестве моделей часто рассматривают центральные моменты функции. Центрированной случайной величиной называется случайная величина 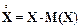. Для непрерывной случайной величины центральная моментная функция k–го порядка определяется по формуле

.

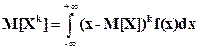Для многомерной случайной величины центральные моменты функции определятся по формуле

,

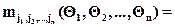
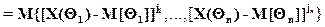которые являются моментными функциями центрированной случайной функции многих параметров.

Среди моментных функций особое значение имеют функции первых двух порядков, которые могут иметь обозначения:

m(Q)=m₁(Q₁)=MX(Q),

R₁(Q₁,Q₂)=m₁(Q₁,Q₂)=M{[X(Q₁)–m(Q₂)][X(Q₂)–m(Q₂)]}.

Функции m(Q) называются средним значением или математическим ожиданием, а R₁(Q₁,Q₂) - корреляционной функцией. При Q₁=Q₂=Q корреляционная функция дает дисперсию s(Q) величины e(Q), R₁(Q₁,Q₂)=s²(Q).

Величину

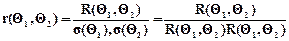
называют коэффициентом корреляции случайных величин X(Q₁) и X(Q₂).