Решение практических задач
№1 Построить геометрическую реализацию графов, представленных матрицами смежности:
а)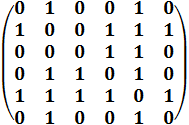 б)
б)
№2 Построить геометрическую реализацию ориентированных графов, представленных матрицами инцидентности:
а)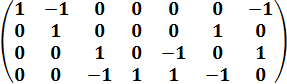 б)
б)
№3 На одной улице жило три друга , отчество которых не начинается с той же буквы что и имя, их звали : Иван, Василий и Семён. У каждого из них дома жил пёс. Хозяевами собак являлись отцы этих, живших на одной улице, друзей. Отцов звали: Игорь, Виталий и Станислав. Известно что собак звали также: Игорь, Виталий и Стасик, но хозяин и его питомец имели разные имена. Известно также что Игорь не Отец Семёна и собаку отца Ивана звали Василий. Какая собака жила в доме у Семёна?
7Гамильтовы графы
Определение. Цепь графа называется гамильтоновой, если это простая цепь (т.е. без петель и кратных ребер), проходящая через все вершины по одному разу.
Пусть G – конечный связный граф. G называется гамильтоновым графом, если существует цикл (гамильтоновый), проходящий через каждую вершину ровно один раз.
Примерами гамильтонова графа являются следующие графы:

Граф называется полугамильтоновым , если в нем существует гамильтоновая цепь. Примерами негамильтонова графа и полугамильтонова графа являются графы:

С гамильтоновыми графами связана следующая задача:
Можно ли перевести шахматного коня с клетки α1 на клетку h8, побывав при этом на каждой клетке шахматной доски ровно один раз? (Клетки α1 и h8 – крайние клетки большой диагонали шахматной доски)
Решение: Построим граф G по следующему правилу. Каждой клетке шахматной доски поставим в соответствие вершину графа. Две вершины соединим ребром тогда и только тогда, когда конь может перейти из клетки, соответствующей одной вершине, в клетку, соответствующую второй. Если конь находится в клетке какого-то цвета, то, сделав ход, он попадает в клетку другого цвета. Поэтому граф G будет двудольным графом. Его доле A будут соответствовать 32 черные клетки, а доле B – 32 белые.
Существования нужного маршрута перевода коня из α1 в h8 эквивалентно существованию в графе G гамильтоновой цепи, соединяющей вершины, соответствующие клеткам α1 и h8.
Покажем, что существования такой цепи невозможно. Действительно, цепь должна иметь 63 ребра, так как для требуемого перехода из α1 в h8 нужно сделать 63 хода. Каждое нечетное ребро (в том числе и 63 - е) цепи, которая начинается в вершине доли A, приводит в долю B. Это эквивалентно тому, что каждый нечетный ход коня, в том числе и 63 – й, приводит в белую клетку. Поскольку клетка h8 черная, то нужный маршрут коня не существует.
К сожалению, в отличие от эйлеровых графов, для гамильтоновых графов нет теоремы, претендующей на полное описание таких графов. Приведем, однако, следующий результат.
7.1Теорема Дирака
Теорема:(Г. Дирак, 1952). Пусть G=(V, E) – простой конечный граф порядка n ≥ 3 такой, что степень каждой вершины ≥ n/2. Тогда G – гамильтонов граф.
Доказательство: Если граф G не является гамильтоновым, то его можно достроить до гамильтонова графа G1 , добавив некоторое конечное число вершин b1, b2, ……., bk и соединив их со всеми вершинами {α1, ……., αn} графа G. При этом можно считать, что k > 0 и k является минимальным с этим свойством. Пусть α1 → b1→ αi→ …→ α1 - гамильтонов цикл в G1. Вершина αi не является смежной с α1 в графе G1, иначе бы мы не использовали вершину b1 (а это противоречило бы минимальности k). Предположим, что существует вершина смежная с αi , которая следует (в нашем цикле) за вершиной x, смежной с α1:
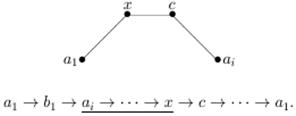
Тогда заменим последний цикл на цикл

который отличается от предыдущего обратной ориентацией прохода в выделенной части. Противоречие с минимальностью k (мы не использовали b1!). Число вершин графа G1 , не являющихся смежными с αi, не меньше числа вершин, смежных с α1 (т.е.≥ n/2+k), т.к. в нашем цикле за каждой смежной с α1 следует некоторая вершина, не являющаяся смежной с αi. С другой стороны, число вершин смежных с αi ≥ n/2+k. Поэтому порядок графа G1 не меньше числа n + 2k. Противоречие доказывает теорему.
Вот пример гамильтонова графа, определяемого по теореме Дирака:
Очевидно, этот граф - гамильтонов. А вот пример гамильтонова графа, не являющегося графом Дирака:
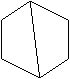
Пример графа, когда не выполняется условие теоремы Дирака, но граф является гамильтоновым.
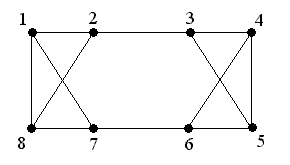
N = 8; d(vi) = 3; 3 ≥ 8/2 = 4 не гамильтонов граф, но существует гамильтонов цикл: M = (1, 2, 3, 4, 5, 6, 7, 8, 1)
8Операции над графами.
Пусть 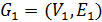 и
и  - графы. Объединением
- графы. Объединением 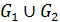 графов
графов  и
и 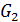 называется граф
называется граф  .
.
Если 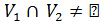 , то пересечением
, то пересечением  графов
графов  и
и 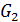 называется граф
называется граф  .
.
Кольцевой суммой  графов
графов  и
и 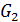 называется граф
называется граф  , где
, где  .
.
Пример:
Для графов 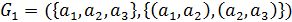 и
и  найдем
найдем 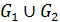 ,
, 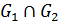 ,
,  . По определению имеем
. По определению имеем  ,
, 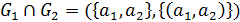 ,
,  .
.

Соединением 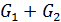 графов
графов  и
и 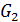 называется граф
называется граф 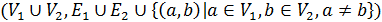 .
.
Пример:
Для графов  и
и 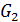 соединением является граф
соединением является граф 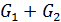 :
:

Произведением 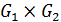 графов
графов  и
и 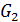 называется граф
называется граф 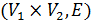 , в котором
, в котором  тогда и только тогда, когда
тогда и только тогда, когда 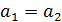 и
и 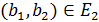 , или
, или  и
и 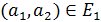 .
.
Пример:
На рисунке изображено произведение 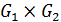 графов
графов 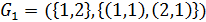 и
и 
