Основные определения.

1. Графы.

1.1 Основные определения.

1.2 Способы задания графов

1.3 Типы графов

1.4 Теоремы о количестве ребер и вершин.

1.5Компоненты связности графа.

2. Геометрическая реализация графов.

2.1Теорема о реализации в трехмерном евклидовом пространстве.

2.2Граф отображения.

2.3Теорема о подобии преобразований множества Х.

3. Эйлеров граф.

3.1Теорема (формула Эйлера) и 2 ее следствия

3.2Алгоритм Флери

3.3Деревья и лес

3.4 Теорема о различных определениях дерева.

4. Изоморфизм и гомеоморфизм графов.

4.1 Подразбиения (подразделения) графа.

4.2 Построить все неизоморфные графы с 3-мя вершинами.

5. Планарность графов.

5.1Теорема(Графы К(3,3) и К(5) не планарны)

5.2Теорема Понтрягина – Куратовского (доказательство необходимости)

5.3Теорема (о планарности графов)

5.4 Хроматическое число графа.

5.5Доказать, что вершины любого планарного графа можно правильно раскрасить в не более чем пять цветов и что трех цветов - мало. 5.6Цикломатическое число.

6. Представление графов в виде матрицы смежности (инцидентности). 6.1Теорема об изоморфизме графов.

7. Гамильтонов граф.

7.1Теорема Дирака.

8. Операции над графами

 

 

1. Графы

 

1.1 Основные понятия

 

1 Графом называется произвольное множество элементов V и произвольное семейство пар E из V, и обозначается G=(V,E). Будем называть V(G)-"множеством вершин", а E(G) — семейством ребер графа. Слово «семейство» употребляется по причине допущения кратных рёбер.

 

2 Если элементы из Е рассматриваются как неупорядоченные пары, то граф называется неориентированным, а пары называются рёбрами Если же элементы из E рассматривать как упорядоченные, то граф ориентированный(орграф), а пары — дуги.

3 Две вершины называются смежными, если они соединяются ребром.

4 Пара вида (a, a) называется петлёй, если пара (a, b) встречается в семействе E несколько раз, то она называется кратным ребром (кратной дугой).

5 Инцидентность. Если v1,v2 — вершины, а e = (v1, v2) — соединяющее их ребро, тогда вершина v1 и ребро e инцидентны, вершина v2 и ребро e тоже инцидентны.Степень вершины есть число входящих в неё ребер(deg v).

 

6 Изолированная вершина — вершина, степень которой равна 0 (то есть dev(v) = 0).

7 Подграфграфа G = (V, E) - граф G1 = (V1, E1), если V1 ⊆V, E1 ⊆E

8 Смежные вершины графа - вершины графа, соединенные ребром.

9 Степенью вершины (deg v) называется количество рёбер, инцидентныхданной вершине. Для псевдографа полагают учитывать петлю дважды.

10 Смежность. Два ребра, инцидентные одной вершине, называются смежными; две вершины, инцидентные одному ребру, также называются смежными

11 Путём в графе G = (V, E) называется любая последовательность вида

v0, (v0, v1), v1, (v1, v2), …, vn – 1, (vn – 1, vn), vn.

Число n в данных обозначениях называется длиной пути.

12 Замкнутый путь если v0 = vn.

13 Цепью называется путь, в котором нет повторяющихся рёбер.

14 Цикл – путь, если он замкнут, и рёбра в нём не повторяются.

15 Простой цепью называется путь без повторения вершин.

16 Простой цикл - путь, если v0 = vn и вершины не повторяются.

 

 

1.2Способы задания графа

Рассмотрим различные способы задания для одного и того же графа:

1) Явное задание графа как алгебраической системы:

<{a,b,c,d},{u,v,w,x}; {(u,a),(u,b),(v,b),(v,c),(w,c),(w,a),(x,c), (x,d)}>. Так как мы рассматриваем только простые графы, граф нам проще определять как модель, носителем которой является множество вершин, а отношение – бинарное отношение смежности вершин. Тогда данный граф запишется как <{a,b,c,d}; {(a,b), (b,a),(b,c),(c,b),(a,c),(c,a),(c,d),(d,c)}>. В таком представлении ребру соответствуют две пары вершин (v1,v2) и (v2,v1), инцидентных данному ребру. Чтобы задать такое представление, достаточно для каждого ребра указать двухэлементное множество вершин – его мы и будем отождествлять с ребром. Для данного графа рёбра задаются множеством {{a,b},{b,c},{a,c},{c,d}} и граф мы будем записывать как пару (V,E), где V – множество вершин, а E – множество рёбер.

 

2) 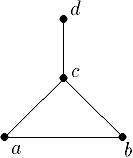Геометрический:

 

 

3) Матрица смежности: графа — это матрица, значения элементов которой характеризуются смежностью вершин графа. При этом значению элемента матрицы присваивается количество рёбер, которые соединяют соответствующие вершины (то есть которые инцидентны обоим вершинам). Петля считается сразу двумя соединениями для вершины, то есть к значению элемента матрицы в таком случае следует прибавлять 2.

 

 

	a	b	c	d
a
b
c
d

 

4) Матрица инцидентности графа — это матрица, значения элементов которой характеризуется инцидентностью соответствующих вершин графа (по вертикали) и его рёбер (по горизонтали). Для неориентированного графа элемент принимает значение 1, если соответствующие ему вершина и ребро инцидентны. Для ориентированного графа элемент принимает значение 1, если инцидентная вершина является началом ребра, значение -1, если инцидентная вершина является концом ребра; в остальных случаях (в том числе и для петель) значению элемента присваивается 0.

	u	v	x	y
a
b
c
d

 

1.3Типы графов

 

 

1 Простой граф — граф, в котором нет кратных рёбер и петель.

2 Полный граф — граф, в котором для каждой пары вершин , существует ребро, инцидентное и инцидентное (каждая вершина соединена ребром с любой другой вершиной).(прямая, треугольник, ромб с диагоналями)

3 Планарный граф — граф, который может быть изображен на плоскости без пересечения ребер.

4 Плоский граф — граф, уложенный на плоскость(т.е его можно на ней нарисовать без пересечения ребер). Граф называется планарным, если он изоморфен некоторому плоскому графу.

5 Регулярный граф — граф, степени всех вершин которого равны. Степень регулярности является инвариантом графа и обозначается . Для нерегулярных графов не определено

6 Регулярный граф степени 0 (вполне несвязный граф, пустой граф, нуль-граф) — граф без рёбер.

7 Двудольный граф (или биграф, или чётный граф) — это граф , такой что множество вершин V разбито на два непересекающихся подмножества V₁ и V₂ , причём всякое ребро E инцидентно вершине из V₁ и вершине из V₂ (то есть соединяет вершину из V₁ с вершиной из V₂ ). Двудольный граф называется «полным», если любые две вершины из V₁ и V₂ и являются смежными. Если | V₁| = а ,| V₂|=b, то полный двудольный граф обозначается К_a,b .

8 Мультиграф - граф, в котором существует пара вершин, которая соединена более чем одним ребром (ненаправленным), либо более чем двумя дугами противоположных направлений

9 Псевдограф– граф, в котором содержаться петли и кратные дуги.

10 Связный граф — граф, в котором все вершины связаны.(его нельзя представить в виде объединения 2х графов)

11 Дополнение графа — граф над тем же множеством вершин, что и исходный, но вершины соединены ребром тогда и только тогда, когда в исходном графе ребра нет.

 

1.4 Теоремы о количестве ребер и вершин.

 

 

Утверждение 1:В любом графе (псевдографе) справедливо следующее

p

соотношение: å deg vi=2q , где p — число вершин, а q — число рёбер.

i =1

Доказательство:Когда мы считаем степень одной вершины, мы считаем все рёбра, вы- ходящие из неё. Вычисляя сумму всех степеней, мы получаем, что каждое ребро считается дважды, так как оно инцидентно двум вершинам (петли по определению степени также посчитаются дважды). Поэтому общая сумма будет равна удвоенному числу рёбер. Утверждение доказано.

 

Утверждение 2.Пусть в G = (V, E) v1 ¹ v2 и пусть P — путь из v1 в v2. Тогда в P можно выделить подпуть из v1 в v2, являющийся простой цепью.

Доказательство:Пусть данный путь — не простая цепь. Тогда в нём повторяется некоторая вершина v, то есть он имеет вид: P1 = v0C1vC2vC3v2. Тогда он содержит подпуть P2 = v0C1vC3v2. Если в P2 повторяется некоторая вершина, то аналогично удалим ещё кусок итак далее. Процесс должен закончиться, так как P1 — конечный путь. Утверждение доказано.

 

Где v-конкатенация.(оп-ция склеивания).

 

 

1.5 компоненты связности графа

Связность. Две вершины в графе связаны, если существует соединяющая их (простая) цепь.

Граф G = (V, E)называется связным, если для любых вершин V_i и V_j принадлежащих V (V_i не равно V_j) существует путь из V_i в V_j

Рассмотрим отношение связности V_i → V_j

1)рефлексивно (V_i → V_i)

2)симметрично (V_i → V_j => V_j → V_i)

3)транзитивно (V_i → V_j и V_j → V_k => V_i → V_k)

=> это отношение эквивалентности

Множество вершин графа разбивается на конечное число классов эквивалентности .

V=V­­₁ ˅…˅V_k ,где V_i∩V_j =0,если i неравно j.

Т.е граф G разбивается на связанные подгруппы ,которые называются компонентами связности.

Лемма 1.Если граф G = (V, E) связный и ребро (a, b) содержится в некотором цикле в графе G, то при выбрасывании из графа G ребра (a, b) снова получится связный граф.

Доказательство.Это утверждение следует из того, что при выбрасывании из графа G

ребра (a, b) вершины a и b всё равно остаются в одной связной компоненте, поскольку из a в b можно пройти по оставшейся части цикла. Лемма доказана.

Лемма 2.Если к связному графу добавить новое ребро на тех же вершинах, то появится цикл.

Доказательство.Рассмотрим произвольный связный граф G = (V, E). Пусть u Î V,

v Î V, (u, v) Ï E. Так как G — связный граф, то в нём есть путь из v в u. Тогда в G есть и простая цепь C из v в u. Поэтому в полученном графе есть цикл C, (u, v), v. Лемма доказана.

 

Лемма 3.Пусть в графе G = (V, E) p вершин и q рёбер. Тогда в G не менее p – q связных компонент. Если при этом в G нет циклов, то G состоит ровно из p – q связных компонент.

Доказательство.Пусть к некоторому графу H, содержащему вершины u и v, добавляется ребро (u, v). Тогда если u и v лежат в разных связных компонентах графа H, то число связных компонент уменьшится на 1. Если u, v лежат в одной связной компоненте графа H, то число связных компонент не изменится. В любом случае, число связных компонент уменьшается не более чем на 1. Значит, при добавлении q рёбер число связных компонент уменьшается не более чем на q. Так как граф G получается из графа G1 = (V, Æ) добавлением q рёбер, то в G не менее p – q связных компонент. Пусть теперь в G нет циклов, и пусть в процессе получения G из G1 добавляется ребро (u, v). Если бы u, v лежали уже в одной связной компоненте, то в G, согласно лемме 2, возникал бы цикл. Следовательно, u, v лежат в разных связных компонентах и при добавлении ребра (u, v) число связных компонент уменьшается ровно на 1. Тогда G состоит ровно из p – q связных компонент. Лемма доказана.

 

 

2Геометрическая реализация графов.

Геометрической реализацией графа , если существует взаимно однозначное соответствие между вершинами фигуры и вершинами графа , а также между кривыми фигуры и ребрами графа такое, что если , то , 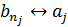. (Т.е. соответствующие кривые и ребра соединяют соответствующие вершины.)

Следовательно, абстрактный граф и его геометрическая реализация являются изоморфными графами, что позволяет вместо конечных абстрактных графов рассматривать только их реализации.(из определения изоморфных графов и определения геометрической реализации)

.

Теорема 1: Каждый конечный граф можно реализовать в трехмерном евклидовом пространстве.

Доказательство:

Пусть граф содержит вершин и ребер. Возьмем прямую и через нее проведем связку из плоскостей. На прямой выберем точек , сопоставим их вершинам графа соответственно . Каждому ребру графа поставим в соответствие плоскость из пучка. Пусть - ребро графа . В плоскости, соответствующей ребру , соединим вершины и дугой окружности. Выполним такое построение для всех ребер графа , получим фигуру. Очевидно, что фигура является геометрической реализацией графа .

 

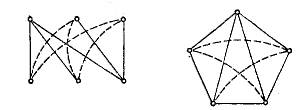
Пример:K_3,3 и К_5.

 

 

3 Эйлеровы графы

Теория графов своим рождением обязана следующей задаче, возникшей в первой половине XVIII столетия и решенной петербургским математиком Эйлером (см. рис.).

Город Кенигсберг (Калининград) расположен на берегах реки Прегель и двух островах. Различные части города были соединены 7 мостами. Можно ли совершить прогулку по городу таким образом, чтобы, выйдя из дома, вернуться обратно, пройдя по каждому мосту только один раз?

Изобразим карту рисунка в виде графа

Эйлер доказал, что не существует маршрута, включающего в себя каждое ребро только один раз. Эйлер поставил более общий вопрос: для каких графов существует цикл (т.е. замкнутая цепь), содержащий все ребра графа, причем каждое ребро в точности по одному разу?

Эйлеровым путем в графе называется путь, содержащий все ребра графа. Эйлеровым циклом в графе называется цикл, содержащий все ребра графа.

Связный граф G называется эйлеровым, если существует замкнутая цепь, проходящая через каждое его ребро. Такая цепь называется эйлеровой цепью. Отметим, что в этом определении требуется, чтобы каждое ребро проходилось только один раз. Если снять ограничение на замкнутость цепи, то граф называется полуэйлеровым, при этом каждый эйлеров граф будет полуэйлеровым.

 

3.1

Теорема 3 (формула Эйлера):Для любой планарной реализации связного планарного графа G = (V, E) с p вершинами, q рёбрами и r гранями выполняется равенство: p – q + r = 2.

Доказательство:Докажем теорему при фиксированном p индукцией по q. Так как

G — связный граф, то q ³ p – 1.

a) Базис индукции: q = p – 1. Так как G — связный и q = p – 1, то согласно теоремы 2

G — дерево, то есть, в G нет циклов. Тогда r = 1. Отсюда p – q + r =

= p – (p – 1) + 1 = 2.

b) Пусть для q: p – 1 £ q < q₀ теорема справедлива. Докажем, что для q = q₀ она также справедлива. Пусть G — связный граф с p вершинами и q₀ рёбрами и пусть в его планарной реализации r граней. Так как q₀ > p – 1, то G — не дерево. Следовательно,

в G есть цикл. Пусть ребро e входит в цикл. Тогда к нему с двух сторон примыкают разные грани. Удалим ребро e из G. Тогда две грани сольются в одну, а полученный граф G1 останется связным. При этом получится планарная реализация графа G1 с p вершинами и q₀ – 1 рёбрами и r – 1 гранями. Так как q₀ – 1 < q₀ , то, по предположению индукции, для G1 справедлива формула Эйлера, то есть p – (q₀ – 1) + (r – 1) = 2, откуда p – q₀ + r = 2. Что и требовалось доказать.

 

Следствие 1:Формула Эйлера справедлива и для геометрической реализации связных графов на сфере.

Доказательство:Пусть связный граф G с p вершинами и q рёбрами реализован на сфере S так, что число граней равно r. Пусть точка A на сфере не лежит на линиях этой геометрической реализации. Пусть P — некоторая плоскость. Поставим сферу S на плоскость P так, чтобы точка A была самой удалённой от плоскости. Спроектируем S на P центральным проектированием с центром в точке A. Тогда на плоскости P мы получим геометрическую реализацию связного графа с p вершинами и q рёбрами, причём число граней будет равно r (грань на сфере, содержащая A, отображается на внешнюю грань на плоскости). По теореме получаем p – q + r = 2. Следствие доказано.

 

Следствие 2:Для любого выпуклого многогранника справедливо равенство p – q + r = 2,

где p — число вершин, q — число рёбер, r — число граней.

Доказательство:Пусть выпуклый многогранник M имеет p вершин, q рёбер и r граней. Пусть O — внутренняя точка многогранника. Разместим сферу S с центром в точке O настолько большого радиуса, чтобы M целиком содержался в S. Рассмотрим центральное проектирование с центром в точке O, и спроектируем вершины и рёбра M на S. Тогда на S мы получим геометрическую реализацию некоторого связного графа с p вершинами, q рёбрами и r гранями. Отсюда согласно следствию 1 p – q + r = 2. Следствие 2 доказано.

3.2Алгоритм Флери построения эйлеровой цепи в эйлеровом графе G

Выходя из произвольной вершины α, идем по ребрам графа, соблюдая правила:

1) стираем ребра по мере их прохождения и стираем изолированные вершины, которые при этом образуются;

2) на каждом этапе идем по мосту (ребро называется мостом, если его удаление нарушает связность графа) только тогда, когда нет других возможностей

Указанный алгоритм действительно работает при прохождении каждой вершины b. Если b≠α, то оставшийся подграф H связан и содержит ровно 2 вершины степени {α, b}. По теореме 2 существует эйлерова цепь T из b и α. Удалим первое ребро этой цепи T. Граф H остается связным и данное рассуждение можно продолжить. Если же b = α, то рассуждаем аналогично

 

Пример: Построим эйлеров цикл для графа

Решение: Это h, {h,l}, l, {l,i}, i, {i,m}, m, {m,j}, j, {j,n}, n, {n,k}, k, {k,h}, h, {h,i}, i, {i,j}, j, {j,k}, k, {k,l}, l, {l,m}, m, {m,n}, n, {n,h}, h.

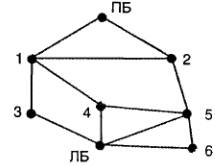
Задача: Шесть островов на реке в парке “Лотос” соединены мостами.

Можно ли, начав прогулку на одном из островов, пройти по каждому из мостиков ровно один раз и вернуться на тот же остров? В случае отрицательного ответа определить, сколько мостиков и между какими островами нужно построить, чтобы такая прогулка стала возможной.

 

Решение: Построим граф G, в котором каждому участку суши поставим в соответствие вершину и соединим две вершины ребром тогда и только тогда, когда соответствующие участки суши будут соединены мостом.

Т. к. связный граф, в котором существует цикл, проходящий через все ребра графа, называется эйлеровым, а сам цикл тоже называется эйлеровым (напомним, что в цикле каждое ребро графа проходит не более раза)

Следовательно, наша задача заключается в определении, будет ли граф G эйлеровым.

Рассмотрим построенный граф G. В этом графе вершины 2 и 4 имеют нечетную степень, следовательно, граф G не является эйлеровым. Это означает, что желаемую прогулку по мостикам совершить нельзя.

Если же соединить ребром вершины 2 и 4, то степень всех вершин нового графа будет четной, а сам граф будет эйлеровым. Поэтому после постройки мостика, соединяющего острова 2 и 4, можно найти маршрут прогулки по мостикам, начинающийся и заканчивающийся в одном месте, при котором каждый мостик будет пройден ровно один раз.

 

Задача 2: Можно ли нарисовать фигуру, изображенную на рис., не отрывая карандаша от бумаги, причем каждую линию фигуры карандаш должен проходить только один раз?

 

 

Решение: Рассмотрим граф, связанный с фигурой:

Степени вершин 1 и 2 графа нечетны. Если мы соединим еще одним ребром эти вершины, то получим эйлеров мультиграф, построим в этом мультиграфе эйлеров цикл. Удалив из цикла добавленное ребро, получим цепь, которая начинается в вершине 1, заканчивается в вершине 2 и содержит каждое ребро графа ровно один раз. Такая цепь называется эйлеровой цепью. Построенная цепь определит движение карандаша при вычерчивании фигуры.

 

3.3 Деревья

Определение 1. Деревомназывается связный граф без циклов.

Определение 2. Подграф G1 = (V1, E1) графа G = (V, E), называется остовным деревом в графе G = (V, E), если G1 = (V1, E1) — дерево и V1 = V.

 

Лемма 1: Если граф G = (V, E) связный и ребро (a, b) содержится в некотором цикле в графе G, то при выбрасывании из графа G ребра (a, b) снова получится связный граф.

Доказательство: Это утверждение следует из того, что при выбрасывании из графа G

ребра (a, b) вершины a и b всё равно остаются в одной связной компоненте, поскольку из a в

b можно пройти по оставшейся части цикла. Лемма доказана.

 

Теорема 1: Любой связный граф содержит хотя бы одно остовное дерево.

Доказательство: Если в G нет циклов, то G является искомым остовным деревом. Если в G есть циклы, то удалим из G какое-нибудь ребро, входящее в цикл. Получится некоторый подграф G1. По лемме 1 G1 — связный граф. Если в G1 нет циклов, то G1 и есть искомое остовное дерево, иначе продолжим этот процесс. Процесс должен завершиться, так как E — конечное множество. Теорема доказана.

 

Теорема 2: Если в связном планарном графе G =(V, E) c p вершинами и q ребрами, отличном от дерева, нет циклов длины меньше k (k≥3), то q ≤ (k/(k-2))(p-2).

Доказательство: Так как по условию qi ³ k, то из леммы получаем 2q ≥ kr и r ≤ 2q/k. Из формулы Эйлера r = 2 – p + q. Отсюда 2-p+q ≤ 2q/k. Далее (k – 2)q £ k(p – 2) и q≤ (k/(k-2))(p-2). Теорема доказана.

 

Следствие: В любом связном планарном графе G = (V, E) без петель и кратных рёбер с

p ³ 3 вершинами и q рёбрами справедливо неравенство: q

£ 3( p – 2).

 

 

3.4 Теорема (о различных определениях дерева): Следующие пять определений эквивалентны (p — число вершин, q — число рёбер):

1) G — дерево;

2) G — без циклов и q = p – 1;

3) G — связный граф и q = p – 1;

4) G — связный граф, но при удалении любого ребра становится несвязным;

5) G — без циклов, но при добавлении любого ребра на тех же вершинах появляется цикл.

Доказательство. Докажем следующие переходы: 1) Þ 2) Þ 3) Þ 4) Þ 5) Þ 1), откуда будет следовать, что из любого условия вытекает любое другое.

1) Þ2): так как G — связный граф и G не содержит циклов, то p – q = 1 по лемме 3. От-

сюда q = p – 1.

2) Þ 3): по лемме 3 в G число связных компонент равно p – q = 1, то есть G — связный граф.

3) Þ4): при удалении одного ребра p – q = 2. Тогда по лемме 3 число связных компонентне менее чем p – q = 2.

4) Þ 5): если G имеет цикл, то согласно лемме 1 можно выбросить одно ребро так, что граф останется связным. Согласно лемме 2, если добавить любое новое ребро к связному графу G на тех же вершинах, то появится цикл.

5) Þ 1): если G не связный граф и вершины u, v лежат в разных связных компонентах графа G, то добавление к G ребра (u, v), очевидно, не порождает циклов, что противоречит

5). Отсюда следует, что G — связный граф. Теорема доказана.

 

 

4 Изоморфизм и гомеоморфизм графов.

 

Два графа G1 и G2 называются изоморфными, если существует взаимно однозначное соответствие между множествами их вершин, обладающее тем свойством, что число ребер, соединяющих любые две вершины в G1, равно число ребер, соединяющих соответствующие вершины в G2.

 

Изоморфизм графов есть отношение эквивалентности. изоморфные графы

 

не изоморфные графы

 

4.1Определение. Операция подразбиения (измельчения) дуги (u, v) в орграфе G = (V, E) состоит в удалении из Е дуги (u, v), добавлении к V новой вершины w и добавлении к Е | {(u, v)} двух дуг (u, v), (w, v). Аналогично определяется операция подразбиения ребра в графах.

 

Определение. Орграф G₁ называется подразбиением орграфа G₂, если орграф G₁ можно получить из G₂ путем последовательного применения операции подразбиения дуг. Аналогично определяется подразбиение графа.

 

Определение. Орграфы G₁, G₂называются гомеоморфными, если существуют их подразбиения, являющиеся изоморфными.

 

 

 

5 Планарность графов.

 

5.1 в эйлере для связного плоского графа справедливо следующее соотношение между количеством вершин , ребер и граней (включая внешнюю грань). p – q + r = 2.

Если каждая грань ограничена не менее чем тремя ребрами(при условии ,что в графе больше двух ребер), а каждое ребро разделяет две грани,то

q≤3p-6, Либо 3r≤2q

 

 

.

K(3,3) К(5)

 

Граф «домики и колодцы» (K3,3)

 

Задача о трёх колодцах. Есть три дома и три колодца. Можно ли так проложить дорожки между домами и колодцами, чтобы от каждого дома к каждому колодцу вела дорожка, и никакие две дорожки не пересекались бы. Мосты строить нельзя.

 

Лемма. Полный двудольный граф с тремя вершинами в каждой из долей (К3,3) нельзя уложить на плоскость.

 

Доказательство. По формуле Эйлера граф имеет 5 граней.

 

С другой стороны: любая грань (включая внешнюю) содержит не менее 4 рёбер. Поскольку каждое ребро включается в ровно две грани, получается соотношение 4r≤2q, r — количество граней, q — количество рёбер. Подставляем в это неравенство r=5 и q=9 и видим, что оно не выполняется.

 

5.2 Теорема (Понтрягина - Куратовского).Граф является планарным тогда и только тогда, когда он не содержит ни одного подграфа, гомеоморфного графам K5 или K3,3.

Доказательство.Необходимость: Пусть G — планарный. Допустим, что он содержит

подграф G1, гомеоморфный графу K5 или K3,3. Рассмотрим планарную реализацию графа G. Удалив лишние вершины и рёбра, мы получим планарную реализацию подграфа G1. Но G1 геометрически — это граф K5 или K3,3 с точками на рёбрах. Если проигнорировать эти точки, то мы получим планарную реализацию графа K5 или K3,3. Но это невозможно в силу теорем 1и 2. Необходимость доказана.

Достаточность без доказательства.

 

5.3

Теорема

Граф планарен тогда и только тогда, если он не содержит подграфов, стягиваемых к К5 или К3,3.

Доказательство

Пусть граф G непланарен, тогда он cодержит подграф Н, гомеоморфный либо графу К5, либо графу К3,3(по теореме Куратовского). Стягивая ребра подграфа… => Предположим, что G содержит подграф Н, стягиваемый к К3,3 и что вершина v графа К3,3 получена стягиванием подграфа Нv…

Задача.

Решение. Любые два участника турнира находятся между собой в одном из двух отношений: они либо уже сыграли между собой, либо еще не сыграли.   Каждому участнику поставим в соответствие вершину графа. Соединим вершины попарно ребрами двух цветов. Пусть ребро…

Решение практических задач

а) б) №2 Построить геометрическую реализацию ориентированных графов, представленных… а)б)