Вибір форми рівняння регресії.

Парна регресія може дати хороший результат при моделюванні, якщо впливом інших факторів, що впливають на об'єкт дослідження, можна знехтувати.

В моделях множинної регресії залежна змінна являється функцією

декількох факторів

Основна мета множинної регресії - побудувати модель з великим числом факторів, визначивши при цьому вплив кожного з них окремо, а також сукупний вплив їх на модельований показник. Множинна регресія широко використовується у вирішенні проблем попиту, прибутковості акцій, при вивченні функції витрат виробництва, в макроекономічних розрахунках і цілого ряду інших питань економетрики.

Побудова рівняння множинної регресії, як і парної регресії, починається з вибору специфікації моделі. Він включає в себе два питання: відбір факторів і вибір виду рівняння регресії.

Відбір факторів.

Фактори, що включаються у множинне регресію, повинні відповідати таким вимогам:

1) Бути кількісно вимірні.

2) Не повинні бути коррелірованни між собою.

Вибір форми рівняння регресії.

Як і в парній залежності, використовуються різні види рівнянь множинної регресії: лінійні і нелінійні.

Зважаючи на чіткої інтерпретації параметрів найбільш широко використовуються лінійна і степенева функції.

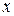У лінійної множинної регресії параметри при називаються коефіцієнтами «чистої» регресії. Вони характеризують середню зміну результату зі зміною відповідного фактора на одиницю при незмінному значенні інших факторів, закріплених на середньому рівні.

У степеневій (мультиплікативній) формі рівняння множинної регресі

має вигляд:

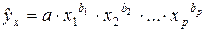Розглянемо звичайну форму лінійного рівняння множинної регресії

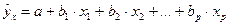Застосувавши МНК , одержимо систему лінійних рівнянь для знаходження

│ ……………………………………………….

│

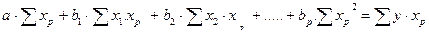
Якщо ввести нові (стандартизовані) зміні

t_y = 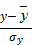; , i = 1,2,……,p

то одержимо рівняння лінійної регресії в стандартизованій формі:

t_y= β₁.t_x₁ + β₂.t_x₂ +………+ β_p.t_xp ,

де β_і =b_i стандартизовані коефіцієнти регресії

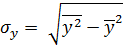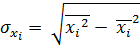
Стандартизовані коефіцієнти регресії показують,на скільки сігм зміниться в середньому результат у, якщо відповідний фактор x_iзміниться на одну сігму

при незмінім середнім рівні інших факторів.

В парній залежності стандартизований коефіцієнт регресії є лінійний коефіцієнт кореляції r_yx Порівнюючи стандартизовані коефіцієнти поміж собою,можна ранжирувати фактори по їх силі впливу на результат.

Тісноту зв^,язку вибранних факторів з досліджуваним результатом можна визначити за допомогою коефіцієнта множинної детермінації R² та середньої похибки апроксимації Ā :

R² = 1 - або R² = ∑β_i.r_yxi

у – ŷ

Ā= ∑ 100 %

Адекватність моделі визначається за допомогою критерія Фішера.

На результати підрахунку коефіцієнтів в моделях багатофакторної регресії

негативно впливає взаємозалежність факторів (мультиколінеарність).

Для оцінки мультиколінеарності факторів можна використати визначник

матриці парних коефіцієнтів кореляції поміж факторами:

1 r_x₁_x₂ ……….r_x₁_xp r_x₂_x₁ 1 ……… r_x₂_xp ……………………………… r_xpx₁ r_xpx₂ ………1

∆r₁₁ =

Чим ближче до одиниці ∆r₁₁ , тим менша мультиколінеарність факторів.

Навпаки, чим ближче ∆r₁₁ до нуля ,тим сильніша мультиколінеарність факторів.

Самим простим методом подолання сильної між факторної кореляції являється виключення із моделі одного або декількох факторів. Із двох факторів , які мають великий коефіцієнт кореляції, виключають той, що має більшу взаємозалежність з другими факторами.

Другим методом подолання сильної між факторної кореляції являється порівняння приросту R² за рахунок включення в модель відповідного фактора:

R²_yx₁_x_2….._xp – R²_yx_2….._xp – за рахунок х1

…………………………………………

R²_yx_1….._xi.._xp – R²_yx_1…._x₍_i_-1)_x₍_i₊₁₎…_xp – за рахунок х_і , де

R²_yx₁_x_2….._xp –коефіцієнт множинної детермінації для моделі з повним набором факторів

R²_yx_1…._x₍_i_-1)_x₍_i₊₁₎…_xp - коефіцієнт множинної детермінації для моделі без включення в модель фактора .

Якщо приріст незначний , то відповідний фактор не включається в модель.

Приклад 1. Припустимо, що залежність витрат на продукти харчування за сукупністю сімей характеризується наступним рівнянням:

де 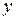- витрати сім'ї за місяць на продукти харчування, тис.руб.;

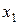- місячний прибуток на одного члена сім'ї, тыс.руб.;

- розмір сім'ї, людин.

Висновки, отримані при аналізі даного рівняння:

1) із зростанням прибутку на одного члена сім'ї на 1 тис.руб. витрати на харчування зростуть в середньому на 350 руб. при тому ж середньому розмірі сім'ї. Тобто, 35% додаткових сімейних витрат витрачається на харчування.

2) збільшення розміру сім'ї при тому же її прибутку передбачає додаткове зростання витрат на харчування на 730 руб.

Параметр не має економічної інтерпретації, тому що формально його значення дорівнює значенню 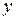прі 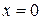, чого практично не буває.

У степеневої функції 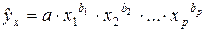коефіцієнти 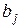є коефіцієнтами еластичності. Вони показують, на скільки відсотків у середньому змінюється результат зі зміною відповідного фактора на 1% при незмінності дії інших факторів. Цей вид рівняння регресії отримав найбільше поширення у виробничих функціях, в дослідженнях попиту і споживання.

Приклад 2. Припустимо, що при дослідженні попиту на м'ясо отримано рівняння

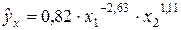або ,

де 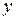- кількість запитуваного м'яса;

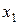- ціна;

-прибуток.

Отже, зростання цін на 1% при тому ж прибутку викликає зниження попиту в середньому на 2,63%. Збільшення доходу на 1% обумовлює при незмінних цінах зростання попиту на 1,11%.