Алгоритм методу Зейделя
Вхідні параметри: B та c - матриця B та вектор правої частини c системы x=Bx+c; n- порядок матриці B;
k- число ітерацій; x0 - вектор початкового наближення.
Функція zeid повертає двовимірний масив розмірності kxn; i-й рядок якого – це i-е наближення.


Результат роботи функції zeid - 10 перших наближень 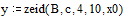

3.7 Оцінка похибки і міра обумовленості
Припустимо, що матриця системи лінійних рівнянь і вектор правих частин задані неточно і замість пред'явленої до розв’язку системи
AХ=b (3.30)
у дійсності розв’язується деяка інша система
A1X=b1, (3.31)
де A1=A+ ,b1=b+
,b1=b+ . Позначимо розв’язки (3.30) і (3.31) через X і X1 відповідно. Оцінимо похибку розв’язку z = X1 - X. Підставимо вирази для A1, b1 і X1 у (3.31)
. Позначимо розв’язки (3.30) і (3.31) через X і X1 відповідно. Оцінимо похибку розв’язку z = X1 - X. Підставимо вирази для A1, b1 і X1 у (3.31)
(A+ ) (X+z) = b +
) (X+z) = b +  .
.
Віднімаючи (3.30), одержимо
A z +  .x +
.x +  .z =
.z =  ,
,
z = A-1 ( -
-  .x -
.x - . z ),
. z ),
||z||<=||A-1||.(|| || + ||
|| + || || . ||x|| + ||
|| . ||x|| + || || ||z||). (3.32)
|| ||z||). (3.32)
Якщо малі || || і ||
|| і || ||, то варто очікувати і малості ||z||. Тоді доданок
||, то варто очікувати і малості ||z||. Тоді доданок  .z має більш високий порядок малості. Звідси випливає оцінка похибки
.z має більш високий порядок малості. Звідси випливає оцінка похибки
 . (3.33)
. (3.33)
Досить поширений випадок, коли похибка матриці системи істотно менша похибки правої частини; як модель цієї ситуації будемо розглядати випадок точного задання матриці системи. Тоді, вважаючи  = 0 у (3.33), маємо
= 0 у (3.33), маємо
||z||<=||A-1||. || ||. (3.34)
||. (3.34)
Для якісної характеристики зв'язку між похибками правої частини і розв’язку вводиться поняття обумовленості матриці системи. Абсолютні похибки правої частини і розв’язку системи залежать від масштабів, якими вимірюються ці величини і матриця системи. Тому правильніше характеризувати властивості системи через зв'язок між відносними похибками правої частини і розв’язку. Для відносної похибки розв’язку з (3.34) маємо
 . (3.35)
. (3.35)
Підставляючи оцінку для ||x|| у (3.35), маємо
 . (3.36)
. (3.36)
Величину ||A-1