Нтерполювання за Лагранжем
За цією методикою попередньо визначають допоміжні поліноми  -го порядку
-го порядку  такі, що
такі, що
 . (5.2)
. (5.2)
Тобто кожен із них набуває значення 1 тільки при  , а для решти заданих значень аргумента він дорівнює нулю. Такі поліноми одержали назву лагранжевих коефіцієнтів, або множників впливу відповідних вузлів інтерполювання.
, а для решти заданих значень аргумента він дорівнює нулю. Такі поліноми одержали назву лагранжевих коефіцієнтів, або множників впливу відповідних вузлів інтерполювання.
Щоб виконувалася перша умова (5.2), поліном  повинен мати такий вигляд
повинен мати такий вигляд
 , (5.3)
, (5.3)
тобто добутку  різниць між поточним значенням аргумента й одним із заданих, окрім
різниць між поточним значенням аргумента й одним із заданих, окрім  -го, з деяким коефіцієнтом
-го, з деяким коефіцієнтом 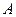 . Друга умова (5.2) дозволяє визначити цей коефіцієнт
. Друга умова (5.2) дозволяє визначити цей коефіцієнт 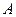 . Для цього в (5.3) слід покласти
. Для цього в (5.3) слід покласти  і прирівняти результат до одиниці. З цього матимемо
і прирівняти результат до одиниці. З цього матимемо
 .
.
Враховуючи це, одержимо остаточний вигляд допоміжного полінома
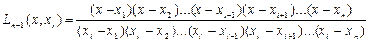 .(5.4)
.(5.4)
Тепер шуканий інтерполюючий поліном можна подати у вигляді


 +
+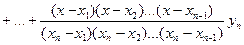 . (5.5)
. (5.5)
Це і є інтерполяційний поліном Лагранжа степеня 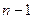 . Кількість арифметичних операцій для його обчислення дорівнює
. Кількість арифметичних операцій для його обчислення дорівнює 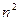 . Інтерполювання за Лагранжем зручно використовувати тоді, коли ведеться багаторазове інтерполювання різних функцій за однакових значень масиву аргументів. Тоді можна заздалегідь одноразово обчислити коефіцієнти Лагранжа, оскільки вони не залежать від функції, що інтерполюється.
. Інтерполювання за Лагранжем зручно використовувати тоді, коли ведеться багаторазове інтерполювання різних функцій за однакових значень масиву аргументів. Тоді можна заздалегідь одноразово обчислити коефіцієнти Лагранжа, оскільки вони не залежать від функції, що інтерполюється.
Розглянемо деякі часткові випадки.
1 Лінійна інтерполяція
У цьому разі маємо 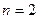 два вузли інтерполяції. Інтерполяційний поліном Лагранжа має вигляд:
два вузли інтерполяції. Інтерполяційний поліном Лагранжа має вигляд:
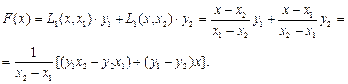 (5.6)
(5.6)
2 Квадратична інтерполяція
У цьому випадку є три вузли інтерполяції ( ). Інтерполяційний поліном Лагранжа набирає вигляду:
). Інтерполяційний поліном Лагранжа набирає вигляду:
 (5.7)
(5.7)