Метод Рунге-Ромберга
Загальна ідея методу така: маємо деяку наближену формулу  (х,к) для обчислення величини z(х) за її значеннями на рівномірній сітці з кроком h, а залишковий член цієї формули
(х,к) для обчислення величини z(х) за її значеннями на рівномірній сітці з кроком h, а залишковий член цієї формули
 . (6.14)
. (6.14)
Наприклад,  ,
,  —задана функція. Нехай
—задана функція. Нехай 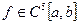 ,
,  ,
,
 ,
,
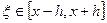 . Тут p = 2. Якщо скористатися тією самою наближеною формулою для обчислення значення z в точці х, але використовуючи сітку з кроком rh, дістанемо
. Тут p = 2. Якщо скористатися тією самою наближеною формулою для обчислення значення z в точці х, але використовуючи сітку з кроком rh, дістанемо
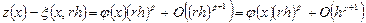 (6.15)
(6.15)
Віднявши (6.14) від (6.15), дістанемо першу формулу Рунгедля оцінки похибки
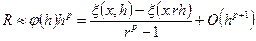 . (6.16)
. (6.16)
Перший доданок у (6.16) є головним членом похибки, тобто розрахунок на другій сітці дає змогу оцінити похибки на першій сітці з точністю до членів вищого порядку. Виключаючи за допомогою (6.16) величину 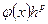 з (6.14), дістанемо другу формулу Рунге
з (6.14), дістанемо другу формулу Рунге
 , (6.17)
, (6.17)
яка дає результат з вищим порядком точності, ніж (6.14). Іноді уточненнярезультату за формулою (6.17) називають уточненням за Річардсоном. Розглянемо приклади застосування описаного вище процесу для підвищення точності в задачі чисельного диференціювання.
Приклад 1 Нехай функція  задана таблицею. Обчислити у' (3).
задана таблицею. Обчислити у' (3).
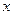
| 
|
| 0,000 0,301 0,478 0,602 0,699 |
Розв’язання. Скориставшись формулою 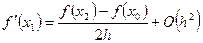 при
при 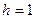 , дістанемо
, дістанемо 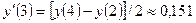 . Збільшуючи крок удвічі (
. Збільшуючи крок удвічі ( ), дістанемо
), дістанемо  .
.
За формулою (6.16) при р = 2  , що лише на 2% відрізняється від шуканого значення у'(3)= 0,145.
, що лише на 2% відрізняється від шуканого значення у'(3)= 0,145.
Приклад 2 За допомогою методу Рунге вивести формулу чисельного диференціювання порядку  з формули більш низького порядку
з формули більш низького порядку  .
.
Розв’язання. Маємо
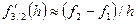 ,
,  .
.
Порядок точності цих формул  , а коефіцієнт збільшення кроку
, а коефіцієнт збільшення кроку 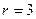 , тому уточнення за методом Рунге дає формулу
, тому уточнення за методом Рунге дає формулу
 .
.
Як бачимо, для обчислення результату більш високого порядку точності не обов'язково використовувати безпосередньо формули високого порядку точності; можна виконати обчислення за простими формулами низької точності на різних сітках і потім уточнити результат за методом Рунге. Такий спосіб має перевагу ще й тому, що величина поправки (6.16) дає апостеріорну оцінку точності.
Метод Рунге узагальнюється на довільну кількість сіток.
Приклад 3 За допомогою розвинення в ряд Тейлора для функції  і
і  дістаємо
дістаємо
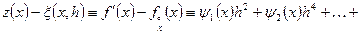
 .
.  !
!
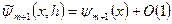 ,
,  . (6.18)
. (6.18)
Приклад 4 Для односторонньої різницевої похідної  при
при  ,
,  маємо
маємо
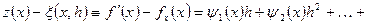
 ,
, 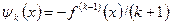 !,
!,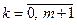 .
.
Нехай розрахунки виконано на  різних сітках
різних сітках  . Тоді із залишкового члена (6.18) можна вилучити
. Тоді із залишкового члена (6.18) можна вилучити 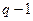 складових. Для цього перепишемо (6.18) у вигляді
складових. Для цього перепишемо (6.18) у вигляді
 ,
, 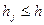 ,
,  .
.
Це система лінійних рівнянь відносно величин  і
і 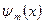 ,
, 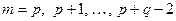 . Використавши формули Крамера, дістанемо уточнений розв'язок за формулою Ромберга
. Використавши формули Крамера, дістанемо уточнений розв'язок за формулою Ромберга
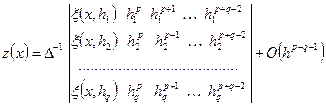 , (6.19)
, (6.19)
де 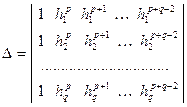 .
.
Ця формула виражає  через обчислені зточністю до
через обчислені зточністю до 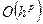 величини
величини  з більш високою точністю
з більш високою точністю 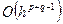 (тобто розрахунок на кожній новій сітці дає змогу підвищити порядок точності на одиницю). Розкладаючи визначник за першим стовпчиком, формулу для
(тобто розрахунок на кожній новій сітці дає змогу підвищити порядок точності на одиницю). Розкладаючи визначник за першим стовпчиком, формулу для  можна записати також у вигляді
можна записати також у вигляді  ,
,
де  .
.
Функції  мають, очевидно, такі дві властивості:
мають, очевидно, такі дві властивості:
а) 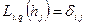 ,
, 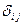 - символ Кронекера;
- символ Кронекера;
б) 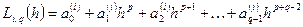 - дійсні коефіцієнти, тобто
- дійсні коефіцієнти, тобто  є многочленами від
є многочленами від 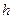 . Тому функція
. Тому функція
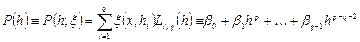 (6.20)
(6.20)
є інтерполюючою функцією для 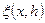 (
(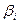 - дійсні коефіцієнти), а величина
- дійсні коефіцієнти), а величина 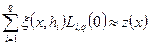
є значенням цієї функції при 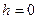 , причому
, причому 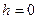 не належить найменшому інтервалу
не належить найменшому інтервалу  , що охоплює всі точки
, що охоплює всі точки  . З цієї причини у випадку методу Рунге - Ромберга говорять також про екстраполяцію. Вживають також терміни «екстраполяція за Річардсоном», «екстраполяція до нуля», «екстраполяція до кроку нуль».
. З цієї причини у випадку методу Рунге - Ромберга говорять також про екстраполяцію. Вживають також терміни «екстраполяція за Річардсоном», «екстраполяція до нуля», «екстраполяція до кроку нуль».
Оскільки система функцій  не при всіх
не при всіх  і не на довільному інтервалі буде системою Чебишева, то інтерполяційна функція (6.20) існує не для будь-якої послідовності
і не на довільному інтервалі буде системою Чебишева, то інтерполяційна функція (6.20) існує не для будь-якої послідовності 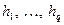 . Але для послідовностей, які найчастіше трапляються на практиці, а саме:
. Але для послідовностей, які найчастіше трапляються на практиці, а саме:
а) 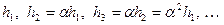 (послідовність Рунге - Ромберга);
(послідовність Рунге - Ромберга);
б)  можна довести, що
можна довести, що  , і тим самим існування многочлена Р(х) гарантується.
, і тим самим існування многочлена Р(х) гарантується.