Зауваження
1 Формула Рунге - Ромберга має ту перевагу, що вона може бути застосована для довільних кроків 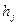 та числа сіток
та числа сіток  (за умови
(за умови  ). Недоліком її є те, що потрібно розв'язувати систему лінійних алгебраїчних рівнянь і в проміжних розрахунках не контролюється точність.
). Недоліком її є те, що потрібно розв'язувати систему лінійних алгебраїчних рівнянь і в проміжних розрахунках не контролюється точність.
2 Метод Ромберга можна застосувати не лише для розкладання вигляду  з функціями
з функціями 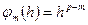 , як в (6.18), але й для довільних функцій
, як в (6.18), але й для довільних функцій 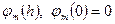 . Коли
. Коли  , що часто трапляється на практиці, тоді інтерполяційний многочлен
, що часто трапляється на практиці, тоді інтерполяційний многочлен 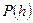 має вигляд
має вигляд
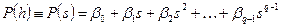 ,
, 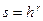
і може бути обчислений в точці  за допомогою, наприклад, алгоритму Ньютона без розв'язування системи.
за допомогою, наприклад, алгоритму Ньютона без розв'язування системи.
3 Якщо сітки такі, що  , тобто згущення їх відбувається за одну і ту саму кількість разів, то зручніше застосувати рекурентно метод Рунге. Це робиться таким чином. Спочатку на кожній парі сіток
, тобто згущення їх відбувається за одну і ту саму кількість разів, то зручніше застосувати рекурентно метод Рунге. Це робиться таким чином. Спочатку на кожній парі сіток  методом Рунге вилучають головний член похибки
методом Рунге вилучають головний член похибки  . Уточнені значення, таким чином, групуються в пари і далі вилучається похибка наступного порядку
. Уточнені значення, таким чином, групуються в пари і далі вилучається похибка наступного порядку 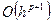 . Всього можна виконати
. Всього можна виконати 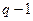 уточнень. При кожному уточненні за формулою (6.16) обчислюється апостеріорна оцінка точності.
уточнень. При кожному уточненні за формулою (6.16) обчислюється апостеріорна оцінка точності.
4 Якщо формула для обчислення 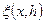 має симетричний вигляд, то на рівномірній сітці часто всі непарні члени ряду (6.18) перетворюються на нуль (див. приклад 3). У такій ситуації користуватися формулою (6.19) невигідно. Потрібно залишити в сумі (6.18) члени
має симетричний вигляд, то на рівномірній сітці часто всі непарні члени ряду (6.18) перетворюються на нуль (див. приклад 3). У такій ситуації користуватися формулою (6.19) невигідно. Потрібно залишити в сумі (6.18) члени 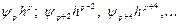 і відповідно змінити формулу Ромберга. Те саме стосується і рекурентної процедури Рунге - при черговому вилученні порядок точності підвищується на 2, а не на 1.
і відповідно змінити формулу Ромберга. Те саме стосується і рекурентної процедури Рунге - при черговому вилученні порядок точності підвищується на 2, а не на 1.
5 Число членів суми (6.18) пов'язане з кількістю неперервних похідних у функції, для якої обчислюються  і
і 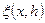 (див. приклади 4, 5). Для не досить гладких функцій недоцільно брати велике число сіток для уточнення. Практично навіть для гладких функцій використовують не більше 3 – 5 сіток, причому, як правило, беруть відношення
(див. приклади 4, 5). Для не досить гладких функцій недоцільно брати велике число сіток для уточнення. Практично навіть для гладких функцій використовують не більше 3 – 5 сіток, причому, як правило, беруть відношення  кроків сіток, що дорівнює 2.
кроків сіток, що дорівнює 2.
6 Метод Рунге - Ромберга можна застосувати лише тоді, коли правильне (6.18), причому коефіцієнти 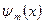 однакові для всіх сіток. Для формул чисельного диференціювання ці коефіцієнти залежать від положення вузлів сітки. Але якщо вибрані конфігурації вузлів на всіх сітках подібні відносно точки х, то залежність від вузлів однакова. У такому разі метод Рунге - Ромберга можна застосувати, в інших випадках його застосувати неможливо. Тому при чисельному диференціюванні метод Рунге - Ромберга застосовується лише для знаходження похідних у вузлах або в середніх точках інтервалів рівномірних і на деяких «близьких» до них сітках. Це так звані квазірівномірні сітки, які добирають так, щоб «найкращим чином» передати поведінку конкретної функції. Сітка (у змінних х) називається квазірівномірною, якщо існує двічі неперервно диференційована функція
однакові для всіх сіток. Для формул чисельного диференціювання ці коефіцієнти залежать від положення вузлів сітки. Але якщо вибрані конфігурації вузлів на всіх сітках подібні відносно точки х, то залежність від вузлів однакова. У такому разі метод Рунге - Ромберга можна застосувати, в інших випадках його застосувати неможливо. Тому при чисельному диференціюванні метод Рунге - Ромберга застосовується лише для знаходження похідних у вузлах або в середніх точках інтервалів рівномірних і на деяких «близьких» до них сітках. Це так звані квазірівномірні сітки, які добирають так, щоб «найкращим чином» передати поведінку конкретної функції. Сітка (у змінних х) називається квазірівномірною, якщо існує двічі неперервно диференційована функція 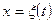 , яка переводить відрізок
, яка переводить відрізок 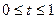 у відрізок
у відрізок  так, що кожній сітці
так, що кожній сітці  відповідає рівномірна сітка
відповідає рівномірна сітка 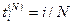 , причому на цьому відрізку
, причому на цьому відрізку  , а
, а 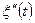 обмежена. Якщо ці умови виконано, то крок сітки
обмежена. Якщо ці умови виконано, то крок сітки  , а різниця двох сусідніх кроків
, а різниця двох сусідніх кроків  , тобто при значній кількості вузлів різниця сусідніх кроків є величина порядку
, тобто при значній кількості вузлів різниця сусідніх кроків є величина порядку  і сусідні інтервали майже рівні (хоча відношення довжин далеких один від одного інтервалів
і сусідні інтервали майже рівні (хоча відношення довжин далеких один від одного інтервалів  може бути великим).
може бути великим).