Квадратурна формула Гауса
Загальний підхід для побудови квадратурної формули для інтегралів 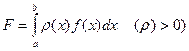 полягає у виборі параметрів
полягає у виборі параметрів  фіксоване) так, щоб забезпечити максимально можливий степінь точності. Квадратурна формула з такою властивістю носить назву формули Гауса. У розглянутих квадратурних формулах вибирали і знаходили вузли та ваги, а отже, тим самим не було використано всі можливості загальної квадратурної формули.
фіксоване) так, щоб забезпечити максимально можливий степінь точності. Квадратурна формула з такою властивістю носить назву формули Гауса. У розглянутих квадратурних формулах вибирали і знаходили вузли та ваги, а отже, тим самим не було використано всі можливості загальної квадратурної формули.
К.Ф.Гаус звернув увагу, що квадратурна формула має  невідомих параметрів
невідомих параметрів  та
та 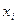 , тобто саме стільки, скільки параметрів має алгебраїчний поліном степеня
, тобто саме стільки, скільки параметрів має алгебраїчний поліном степеня  . Він запропонував підбирати ці параметри так, щоб квадратурна формула була точною для підінтегральної функції
. Він запропонував підбирати ці параметри так, щоб квадратурна формула була точною для підінтегральної функції  у вигляді полінома степеня, не вищого за
у вигляді полінома степеня, не вищого за 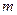 .
.
Спочатку для спрощення розглянемо відрізок 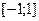 , тобто інтеграл вигляду
, тобто інтеграл вигляду
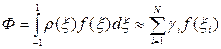 (7.7)
(7.7)
Отже, знайдемо параметри  з таких умов:
з таких умов:
 (7.8)
(7.8)
Це система  нелінійних алгебраїчних рівнянь відносно
нелінійних алгебраїчних рівнянь відносно 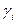 ,
, 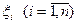 .
.
Для подальшого спрощення вважатимемо, що  .
.
Якщо  одержимо
одержимо 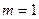 і система
і система 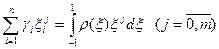 набере вигляду
набере вигляду

із другого рівняння випливає, що 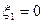 , тобто дійшли відомої формули середніх для відрізка
, тобто дійшли відомої формули середніх для відрізка 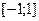

яка є точною для будь-якого полінома 1-го степеня.
Якщо 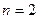 , система
, система  матиме такий вигляд (
матиме такий вигляд ( ):
):


Розв’язавши цю систему, знайдемо:
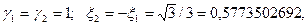
тобто маємо квадратурну формулу
 ,
,
яка є точною для будь-якого полінома 3-го степеня.
За довільного  як вузли квадратурної формули Гауса беруть нулі поліномів Лежандра
як вузли квадратурної формули Гауса беруть нулі поліномів Лежандра
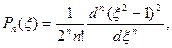
а ваги цієї квадратурної формули визначають за таким виразом:
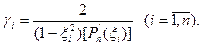 (7.9)
(7.9)
Маючи значення 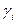 та вузлів
та вузлів 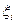 на відрізку
на відрізку  , значення інтеграла на довільному відрізку
, значення інтеграла на довільному відрізку 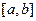 обчислюється за такою квадратурною формулою Гауса:
обчислюється за такою квадратурною формулою Гауса:

Похибка квадратурної формули Гауса має вигляд
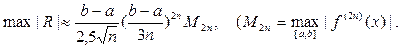
Зауважимо, що, починаючи з  , і вузли, і ваги є ірраціональними числами, а кінці a і b ніколи не входять до вузлів.
, і вузли, і ваги є ірраціональними числами, а кінці a і b ніколи не входять до вузлів.
Іншими прикладами квадратурних формул типу Гауса є формули Чебишева, Ерміта.