Кубатурна формула типу Симпсона
Нехай областю інтегрування є K-вимірний просторовий паралелепіпед 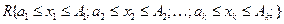 (рис.7.6), сторони якого паралельні осям координат. Кожний із проміжків
(рис.7.6), сторони якого паралельні осям координат. Кожний із проміжків  розіб'ємо навпіл точками:
розіб'ємо навпіл точками:
 , де
, де  .
.
Усього, таким чином, одержимо 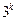 точок сітки. Маємо
точок сітки. Маємо
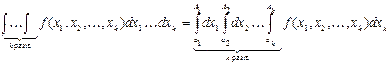 . (7.23)
. (7.23)
Знаходимо K-вимірний інтеграл, обчислюючи кожний внутрішній інтеграл за квадратурною формулою Симпсона на відповідному відрізку. Проведемо повністю всі обчислення для випадку K=2:

Застосовуючи до кожного інтеграла знову формулу Симпсона, одержимо:
 ,
,
або
 (7.24)
(7.24)
Формулу (7.24) будемо називати кубатурною формулою Симпсона. Отже,
 (7.25)
(7.25)
де  – сума значень підінтегральної функції
– сума значень підінтегральної функції 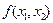 у вершинах прямокутника
у вершинах прямокутника 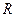 ,
, 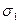 – сума значень
– сума значень 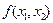 у серединах сторін прямокутника
у серединах сторін прямокутника 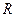 ,
, 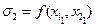 – значення функції
– значення функції 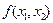 в центрі прямокутника
в центрі прямокутника 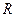 . Кратності цих значень позначені на рис. 7.6.
. Кратності цих значень позначені на рис. 7.6.
Якщо розміри просторового паралелепіпеда 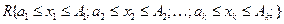 великі, то для збільшення точності кубатурної формули область
великі, то для збільшення точності кубатурної формули область 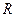
 розбивають на систему паралелепіпедів, до кожного з яких застосовують кубатурну формулу Симпсона.
розбивають на систему паралелепіпедів, до кожного з яких застосовують кубатурну формулу Симпсона.
Знову розглянемо випадок K=2. Покладемо, що сторони прямокутника 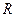 ми розділили відповідно на
ми розділили відповідно на  й
й  однакових частин; у результаті вийшла відносно велика мережа
однакових частин; у результаті вийшла відносно велика мережа 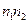 прямокутників (на рис. 7.7 вершини цих прямокутників відзначені більшими кружками). Кожний із цих прямокутників, у свою чергу, розділимо на чотири однакові частини. Вершини цієї останньої дрібної мережі прямокутників візьмемо за вузли
прямокутників (на рис. 7.7 вершини цих прямокутників відзначені більшими кружками). Кожний із цих прямокутників, у свою чергу, розділимо на чотири однакові частини. Вершини цієї останньої дрібної мережі прямокутників візьмемо за вузли 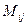 кубатурної формули.
кубатурної формули.
Нехай  і
і 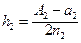 . Тоді мережа вузлів буде мати координати:
. Тоді мережа вузлів буде мати координати:  ;
;

Для скорочення введемо позначення 
Застосовуючи формулу (7.24) до кожного із прямокутників великої мережі, будемо мати (рис.7.7):
 Звідси, виконавши зведення подібних членів, остаточно знаходимо:
Звідси, виконавши зведення подібних членів, остаточно знаходимо:
 (7.26)
(7.26)

де коефіцієнти  є відповідними елементами матриці
є відповідними елементами матриці

Якщо область інтегрування  – довільна, то будуємо паралелепіпед
– довільна, то будуємо паралелепіпед  , сторони якого паралельні осям координат (рис. 7.8). Розглянемо допоміжну функцію
, сторони якого паралельні осям координат (рис. 7.8). Розглянемо допоміжну функцію
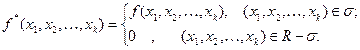
У такому випадку маємо
 Останній інтеграл приблизно може бути обчислений за загальною кубатурною формулою (7.26).
Останній інтеграл приблизно може бути обчислений за загальною кубатурною формулою (7.26).
Питання і завдання до розділу 7
1 Найпростіші квадратурні формули ( прямокутників, трапецій, Симпсона), геометрична ілюстрація, оцінки похибки. Точність квадратурних формул.
2 Квадратурні формули інтерполяційного типу: виведення формул, оцінки похибки.
3 Квадратурні формули Гауса: виведення формул, точність формул.
4 Правило Рунге практичної оцінки похибки. Адаптивні процедури чисельного інтегрування.
5 Обчислити наближено з кроком h=1 інтеграл 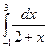 за формулами прямокутників, трапецій, Симпсона. Оцінити похибку теоретично.
за формулами прямокутників, трапецій, Симпсона. Оцінити похибку теоретично.
6 Переконатися в тім, що формула прямокутників є точною для многочленів  , а формула Симпсона – для многочленів
, а формула Симпсона – для многочленів 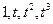 .
.
7 Оцінити теоретично значення кроку інтегрування h для наближеного обчислення інтеграла 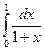 за формулою трапецій з точністю
за формулою трапецій з точністю 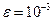 .
.
8 Оцінити теоретично значення кроку інтегрування h для наближеного обчислення інтеграла 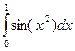 по формулі Симпсона з точністю
по формулі Симпсона з точністю  .
.
9 Одержати квадратурні формули прямокутників і трапецій із загальної формули інтерполяційного типу.
10 Переконатися, що квадратурна формула Гауса з одним вузлом точна для многочленів 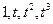 .
.
11 Обчислити інтеграл  за формулами трапецій і Симпсона з точністю
за формулами трапецій і Симпсона з точністю 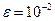 , використовуючи правило Рунге оцінки похибки.
, використовуючи правило Рунге оцінки похибки.
12 Знайти оцінку похибки обчислення інтеграла  за складеною формулою
за складеною формулою
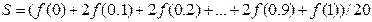 .
.
13 Оцінити мінімальне число розбиттів відрізка N інтегрування для наближеного обчислення інтеграла 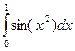 за складеною формулою трапецій, що забезпечує точність
за складеною формулою трапецій, що забезпечує точність  .
.
14 Обчислити інтеграли  , де
, де  , k=0,1,...,5 аналітично й використовуючи квадратурну формулу Симпсона із кроком h = (b-a)/2. Для многочленів якого степеня використовувана квадратурна формула точна й чому? Оцінити похибку інтегрування за правилом Рунге.
, k=0,1,...,5 аналітично й використовуючи квадратурну формулу Симпсона із кроком h = (b-a)/2. Для многочленів якого степеня використовувана квадратурна формула точна й чому? Оцінити похибку інтегрування за правилом Рунге.
15Обчислити значення інтеграла  аналітично й, використовуючи формулу прямокутників із кроками
аналітично й, використовуючи формулу прямокутників із кроками 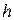 :
:  ,
,  ,…
,…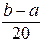 ...(
...(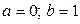 ). При зазначених значеннях
). При зазначених значеннях 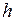 знайти абсолютну похибку й оцінки теоретичної абсолютної похибки. На одному кресленні побудувати графіки знайдених похибок.
знайти абсолютну похибку й оцінки теоретичної абсолютної похибки. На одному кресленні побудувати графіки знайдених похибок.
16Побудувати графік функції  . Для обчислення інтеграла з точністю 10-8 використати квадратурну формулу трапецій і правило Рунге оцінки похибки.
. Для обчислення інтеграла з точністю 10-8 використати квадратурну формулу трапецій і правило Рунге оцінки похибки.
17Обчислити значення інтеграла  із задачі 14, використовуючи квадратурну формулу Гауса з одним, двома, трьома, чотирма вузлами. Визначити абсолютну похибку результату. Побудувати гістограму залежності похибки від числа вузлів. Переконатися, що квадратурні формули Гауса з N+1 (N=0,1,2,3) вузлами точні для многочленів 1, t,…,tm, де m=2N+1.
із задачі 14, використовуючи квадратурну формулу Гауса з одним, двома, трьома, чотирма вузлами. Визначити абсолютну похибку результату. Побудувати гістограму залежності похибки від числа вузлів. Переконатися, що квадратурні формули Гауса з N+1 (N=0,1,2,3) вузлами точні для многочленів 1, t,…,tm, де m=2N+1.
18Обчислити наближено площу фігури, обмеженої кривими 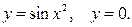 Точки перетину кривих знайти графічно. Для обчислення інтегралів з точністю 10-8 використати квадратурну формулу Симпсона і правило Рунге оцінки похибки.
Точки перетину кривих знайти графічно. Для обчислення інтегралів з точністю 10-8 використати квадратурну формулу Симпсона і правило Рунге оцінки похибки.
19Наближено обчислити подвійний інтеграл по прямокутній області  з точністю 0.001.
з точністю 0.001.
20 Функція y=y(x) задана таблицею своїх значень:
| x | 0.1 | 0.2 | 0.3 | 0.4 | |
| y | 1.2 | 1.24 | 0.76 | 0.6 |
Обчислити наближене значення інтеграла 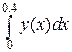 за квадратурними формулами трапецій і Симпсона.
за квадратурними формулами трапецій і Симпсона.
21Побудувати квадратурну формулу  , точну для многочленів найбільш високого степеня, використовуючи метод невизначених коефіцієнтів.
, точну для многочленів найбільш високого степеня, використовуючи метод невизначених коефіцієнтів.
22 Знайти наближене значення інтеграла  із кроком
із кроком  , використовуючи квадратурні формули прямокутників, трапецій, Симпсона. Оцінити похибку формули чисельного інтегрування двома способами: використовуючи теоретичну оцінку похибки та правило Рунге.
, використовуючи квадратурні формули прямокутників, трапецій, Симпсона. Оцінити похибку формули чисельного інтегрування двома способами: використовуючи теоретичну оцінку похибки та правило Рунге.
23 З яким кроком інтегрування потрібно обчислювати наближене значення інтеграла 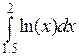 за формулою трапецій для того, щоб забезпечити точність 0.00001.
за формулою трапецій для того, щоб забезпечити точність 0.00001.
Розділ 8
Чисельне розв’язання звичайних диференціальних рівнянь
Звичайними диференціальними рівняннями називаються рівняння, що пов’язують функцію та її похідні з однією незалежною змінною. Якщо незалежних змінних більше, ніж одна, то рівняння називається диференціальним рівнянням з частинними похідними.
За допомогою звичайних диференціальних рівнянь будуються моделі руху систем взаємодіючих часток, електротехнічних процесів у електричних ланцюгах, кінетики хімічних реакцій, процесів заселення рівнів енергії у високотемпературних середовищах і багатьох інших об'єктів і процесів.
До задач для звичайних диференціальних рівнянь зводяться деякі задачі для рівнянь у частинних похідних, коли рівняння дозволяє провести відокремлення змінних (наприклад, при обчисленні енергетичного спектра часток у полях визначеної симетрії).
Звичайне диференціальне рівняння будь-якого порядку за допомогою заміни змінних може бути зведене до системи рівнянь першого порядку.
У загальному вигляді перетворення є таким:
диференціальне рівняння  -го порядку
-го порядку

заміною змінних  зводяться до системи
зводяться до системи  рівнянь першого порядку
рівнянь першого порядку
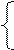

де позначено  .
.
Відповідно до викладеного далі будуть розглядатися системи рівнянь першого порядку:

Розв’язок системи  -го порядку залежить від
-го порядку залежить від  параметрів
параметрів  Єдиний розв’язок визначається при використанні додаткових умов для шуканої функції. У залежності від того, яким чином ставляться такі умови, розрізняють три типи задач для звичайних диференціальних рівнянь: задача Коші, крайова задача і задача на власні значення.
Єдиний розв’язок визначається при використанні додаткових умов для шуканої функції. У залежності від того, яким чином ставляться такі умови, розрізняють три типи задач для звичайних диференціальних рівнянь: задача Коші, крайова задача і задача на власні значення.
У задачі Коші всі додаткові умови ставляться в одній точці  . Розв’язок шукається на деякому інтервалі
. Розв’язок шукається на деякому інтервалі 
Якщо праві частини  рівнянь неперервні в деякому околі початкової точки
рівнянь неперервні в деякому околі початкової точки 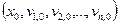 і задовольняють умову Ліпшиця за змінними
і задовольняють умову Ліпшиця за змінними  , то розв’язок задачі Коші існує, єдиний і неперервно залежить від координат початкової точки, тобто задача є коректною. Умова Ліпшиця формулюється в такий спосіб:
, то розв’язок задачі Коші існує, єдиний і неперервно залежить від координат початкової точки, тобто задача є коректною. Умова Ліпшиця формулюється в такий спосіб:
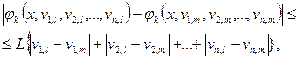
для будь-яких точок  , де
, де 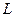 - деяка константа.
- деяка константа.
Можна виділити три класи методів розв’язання звичайних диференціальних рівнянь: точні, наближені та чисельні.
Точні методи передбачають одержання розв’язку у вигляді комбінації елементарних функцій або у вигляді квадратур від останніх. Можливості точних методів обмежені.
Наближені методи зводяться до побудови послідовності функцій  , що мають границею шукану функцію
, що мають границею шукану функцію 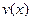 . Обриваючи цю послідовність на якомусь
. Обриваючи цю послідовність на якомусь 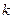 , одержують наближений розв’язок.
, одержують наближений розв’язок.
Найбільш універсальними методами розв’язання є чисельні. Їхній основний недолік - можливість одержання тільки часткового розв’язку.
Варто зауважити, що успіх від застосування чисельного методу суттєво залежить від обумовленості задачі, тобто задача повинна бути добре обумовленою, а саме, малі зміни початкових умов повинні призводити до малих змін у розв’язку. У протилежному випадку (слабкої стійкості) малі похибки в початкових даних або похибки чисельного методу можуть призводити до великих похибок у розв’язку.
Приклад. Рівняння  з початковою умовою
з початковою умовою 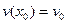 має розв’язок
має розв’язок  .
.
При  виходить розв’язок
виходить розв’язок 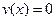 . Якщо припустити, що
. Якщо припустити, що  не дорівнює строго нулеві, а має невелике відхилення від нуля, наприклад,
не дорівнює строго нулеві, а має невелике відхилення від нуля, наприклад,  , тоді при великих
, тоді при великих 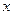 буде мати місце така ситуація.
буде мати місце така ситуація.
Якщо  , то
, то 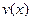 при збільшенні
при збільшенні 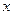 прямує до нуля, тобто до незбуреного розв’язку. У цьому випадку розв’язок називається асимптотично стійким за Ляпуновим.
прямує до нуля, тобто до незбуреного розв’язку. У цьому випадку розв’язок називається асимптотично стійким за Ляпуновим.
Однак при 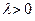 зі збільшенням
зі збільшенням 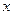
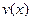 необмежено зростає, а саме, наприклад, при
необмежено зростає, а саме, наприклад, при 
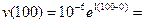
 .
.
Таким чином, розв’язок виявляється нестійким.
Далі будуть розглядатися алгоритми розв’язку задачі Коші на прикладі одного рівняння першого порядку  . Узагальнення на випадок системи
. Узагальнення на випадок системи  рівнянь здійснюється заміною
рівнянь здійснюється заміною 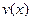 на
на  і
і на
на 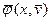 , де
, де
 ,
,  .
.
8.1 Різницева апроксимація диференціальних рівнянь однокроковими методами
Виберемо на відрізку деяку систему  , значень аргумента так, щоб виконувалися співвідношення
, значень аргумента так, щоб виконувалися співвідношення 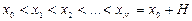 . Множину
. Множину  називають сіткою, точки
називають сіткою, точки 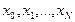 — вузлами сітки, величину
— вузлами сітки, величину 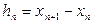 - кроком сітки. Якщо
- кроком сітки. Якщо 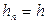 , сітка називається рівномірною, в іншому разі - нерівномірною. Сітковою функцією y=yj=y(xj) називається функція, що задана у вузлах сітки. Будь-яку сіткову функцію yj=y(xj) можна представити у вигляді вектора Y=(y0, y1, ..., yn-1, yn).
, сітка називається рівномірною, в іншому разі - нерівномірною. Сітковою функцією y=yj=y(xj) називається функція, що задана у вузлах сітки. Будь-яку сіткову функцію yj=y(xj) можна представити у вигляді вектора Y=(y0, y1, ..., yn-1, yn).
Нехай маємо диференціальне рівняння Lу(x) = f(x,у) (наприклад, 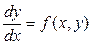 ) , де L – диференціальний оператор.
) , де L – диференціальний оператор.
Замінимо Lу у вузлі сітки xi лінійною комбінацією значень сіткової функції yi на деякій множині вузлів сітки, яка називається шаблоном. Така заміна Lу на Lhyh називається апроксимацією на сітці диференціального оператора L різницевим оператором Lh. Заміна неперервної функції f(x,у) у вузлах сітки на сіткову функцію f(xh,yh) називається апроксимацією правої частини.
У такий спосіб диференціальне рівняння можна апроксимувати (замінити) на сітці різницевою схемою
Lhyh = f(xh,yh) ( наприклад,  ).
).
Вивчення різницевих апроксимацій проводиться спочатку локально, тобто в будь-якому фіксованому вузлі сітки.
При розв’язуванні диференціальних рівнянь чисельним методом основним є питання про збіжність. Стосовно до різницевих методів традиційно більш уживане поняття збіжності при 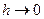 . Позначимо за
. Позначимо за 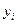 значення сіткової функції, що відповідає значенню точного розв’язку диференціального рівняння
значення сіткової функції, що відповідає значенню точного розв’язку диференціального рівняння 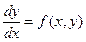 у вузлі
у вузлі  -
-  (
(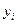 є наближеними значеннями
є наближеними значеннями  ). Збіжність при
). Збіжність при 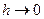 означає таке. Фіксуємо точку
означає таке. Фіксуємо точку 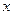 і будуємо сукупність сіток
і будуємо сукупність сіток 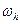 таким чином, що
таким чином, що 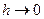 і
і 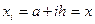 (при цьому
(при цьому 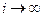 ). Тоді вважають, що чисельний метод збігається в точці
). Тоді вважають, що чисельний метод збігається в точці 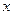 , якщо
, якщо  при
при 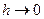 ,
, 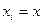 . Метод збігається на відрізку
. Метод збігається на відрізку 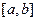 , якщо він збігається в кожній точці
, якщо він збігається в кожній точці  . Вважають, що метод має
. Вважають, що метод має  -й порядок точності, якщо можна знайти таке число
-й порядок точності, якщо можна знайти таке число 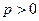 , що
, що  при
при 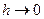 .
.
Уведемо далі поняття нев'язки, або похибки, апроксимації різницевого рівняння, що заміняє задане диференціальне рівняння, на розв’язку вихідного рівняння, тобто нев'язка  являє собою результат підстановки точного розв’язку рівняння
являє собою результат підстановки точного розв’язку рівняння  у різницеве рівняння. Наприклад, рівняння
у різницеве рівняння. Наприклад, рівняння 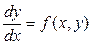
 можна замінити таким найпростішим різницевим рівнянням
можна замінити таким найпростішим різницевим рівнянням
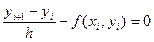 ,
,  .
.
Тоді нев'язка визначиться як 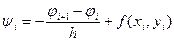 .
.
Наближений розв’язок не збігається з 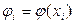 , тому нев'язка
, тому нев'язка  в
в  -ій точці не дорівнює нулеві.
-ій точці не дорівнює нулеві.
Чисельний метод апроксимує вихідне диференціальне рівняння, якщо 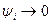 при
при 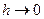 , і має
, і має  -й порядок точності, якщо
-й порядок точності, якщо  .
.
Доведено, що порядок точності чисельного методу розв’язання диференціального рівняння збігається з порядком апроксимації при досить загальних припущеннях.