Метод Ейлера
Ознайомлення з чисельними методами розв’язання звичайних диференціальних рівнянь першого порядку почнемо з вивчення методу Ейлера для задачі Коші

 , (8.1)
, (8.1)
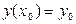 . (8.2)
. (8.2)
Відзначимо, що на практиці цей метод використовується рідко через невисоку точність, однак він є найпростішим з чисельних методів і на його прикладі зручно пояснити їх суть, способи побудови і дослідження.
Для розв’язання задачі потрібно знайти наближені значення  точного розв’язку
точного розв’язку  рівняння (8.1). Уведемо позначення
рівняння (8.1). Уведемо позначення  . Припустимо, що розв’язок
. Припустимо, що розв’язок  задачі (8.1) — (8.2) у вузлі
задачі (8.1) — (8.2) у вузлі 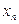 відомий. Знайдемо розв’язок у наступному вузлі
відомий. Знайдемо розв’язок у наступному вузлі  . Використовуючи формулу Тейлора, одержимо
. Використовуючи формулу Тейлора, одержимо
 (8.3)
(8.3)
Відзначимо, що похідну 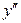 , що стоїть у правій частині, можна знайти, диференціюючи рівняння (8.1).
, що стоїть у правій частині, можна знайти, диференціюючи рівняння (8.1).
Підставимо у формулі (8.3) , тоді
, тоді
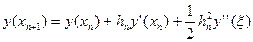 . (8.4)
. (8.4)
Припускаючи, що 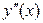 на відрізку
на відрізку 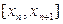 обмежена, маємо
обмежена, маємо  . Однак використовувати формулу (8.4) незручно з таких міркувань:
. Однак використовувати формулу (8.4) незручно з таких міркувань:
1) вираз 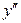 може виявитися громіздким; 2) якщо права частина рівняння (8.1) відома лише приблизно, що часто має місце при розв’язанні технічних задач, знаходити її похідні небажано.
може виявитися громіздким; 2) якщо права частина рівняння (8.1) відома лише приблизно, що часто має місце при розв’язанні технічних задач, знаходити її похідні небажано.
Якщо 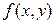 має q-і неперервні похідні по сукупності аргументів, то в розкладанні (8.3) можна враховувати значення членів аж до
має q-і неперервні похідні по сукупності аргументів, то в розкладанні (8.3) можна враховувати значення членів аж до 
Відкидаючи в (8.4) величини другого порядку малості при  в порівнянні з кроком сітки
в порівнянні з кроком сітки 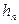 , одержуємо формулу для обчислення наближеного значення
, одержуємо формулу для обчислення наближеного значення  у вузлі
у вузлі 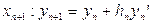 З огляду на те, що
З огляду на те, що  , виводимо розрахункову формулу методу Ейлера
, виводимо розрахункову формулу методу Ейлера
 . (8.5)
. (8.5)
Для чисельного розрахунку за формулою (8.5) досить знати 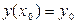 . Потім, використовуючи (8.5), можна послідовно знайти значення розв’язку
. Потім, використовуючи (8.5), можна послідовно знайти значення розв’язку  відповідно в точках
відповідно в точках 

|
Рис. – 8.1
Геометрична інтерпретація методу Ейлера показана на рис. 8.1, де зображена множина інтегральних кривих рівняння (8.1). Використання тільки першого члена формули Тейлора рівносильне заміні інтегральної кривої на відрізку [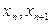 ] дотичною до неї в точці (
] дотичною до неї в точці (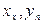 ). На кожному кроці заново визначається дотична, і, отже, траєкторія буде ламаною лінією. Тому метод Ейлера називають також методом ламаних.
). На кожному кроці заново визначається дотична, і, отже, траєкторія буде ламаною лінією. Тому метод Ейлера називають також методом ламаних.
При визначенні наближеного розв’язку задачі надзвичайно важлива оцінка похибки використовуваного методу. Розглянемо таку оцінку для методу Ейлера.
Припустимо, що початкова умова 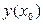 задана точно. При одержанні (8.5) у формулі Тейлора був відкинутий член, що містить
задана точно. При одержанні (8.5) у формулі Тейлора був відкинутий член, що містить 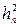 .
.
На першому кроці, при обчисленні 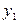 , отримана похибка
, отримана похибка  , яка називається локальною похибкою, або похибкою на кроці.
, яка називається локальною похибкою, або похибкою на кроці.
На другому кроці  обчислюється за формулою
обчислюється за формулою  . Величина
. Величина 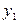 , знайдена раніше, визначена наближено. Тому сумарна похибка на другому кроці
, знайдена раніше, визначена наближено. Тому сумарна похибка на другому кроці 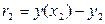 буде викликана не тільки заміною інтегральної кривої на відрізку
буде викликана не тільки заміною інтегральної кривої на відрізку 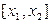 дотичною до неї, але і помилкою, допущеною на першому кроці.
дотичною до неї, але і помилкою, допущеною на першому кроці.
Аналогічно сумарна похибка n-го кроку залежить не тільки від заміни інтегральної кривої на відрізку 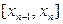 дотичною, але і від помилок, допущених при обчисленні
дотичною, але і від помилок, допущених при обчисленні 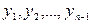 (рис. 8.2). У випадку, коли початкова умова задана неточно, сумарна похибка на будь-якому кроці буде залежати і від похибки початкової умови (8.2).
(рис. 8.2). У випадку, коли початкова умова задана неточно, сумарна похибка на будь-якому кроці буде залежати і від похибки початкової умови (8.2).
Розглянемо похибку наближеного розв’язку  , знайденого методом Ейлера (рис. 8.2).
, знайденого методом Ейлера (рис. 8.2).
Припустимо, що функція f(x, у) з (8.1) неперервна і має неперервні перші похідні в області зміни своїх аргументів. Віднімаючи (8.5) з (8.4) , одержимо
 Використовуючи формулу Тейлора, з урахуванням того, що
Використовуючи формулу Тейлора, з урахуванням того, що  , одержуємо
, одержуємо
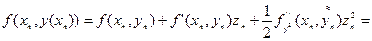
 .
.
Звідси  .
.

Рис. – 8.2
Отже, з точністю до величин більш високого порядку малості,
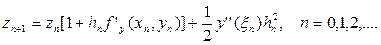
Таким чином,

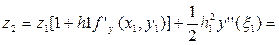
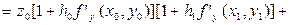
 .
.
Аналогічно
 Продовжуючи цей процес, одержимо
Продовжуючи цей процес, одержимо
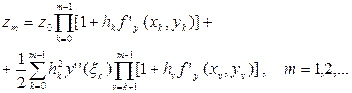 (8.6)
(8.6)
Таким чином, похибка 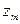 на довільному кроці m виражається через похибку
на довільному кроці m виражається через похибку 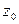 .
.
При малих  має місце така оцінка:
має місце така оцінка:
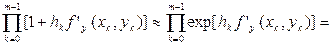
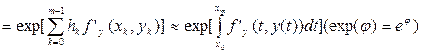 .
.
Аналогічно

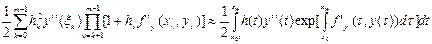 .
.
Тут h(t) – кусково-лінійна функція, значення якої в кожному вузлі 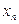 дорівнює
дорівнює 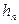 .
.
Підставляючи ці вирази у формулу (8.6), одержимо оцінку похибки на довільному кроці m:
 (8.7)
(8.7)
Вона складається з двох доданків, перший з яких обумовлений похибкою 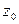 початкових даних. Якщо вони точні,
початкових даних. Якщо вони точні, 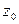 =0, що і будемо припускати надалі.
=0, що і будемо припускати надалі.
Поява другого доданка пов'язана з відкиданням у рівності (8.5) залишкового члена формули Тейлора. Оцінимо цей доданок зверху.
Припустимо, що на відрізку 
 , |
, | , |
, | .
.
Тоді 
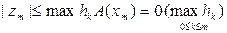 , де (8.8)
, де (8.8)

З нерівності (8.8) випливає твердження.
Якщо f(x,y) неперервна й обмежена в системі зі своїми першими похідними в області зміни своїх аргументів, то наближений розв’язок задачі (8.1) – (8.2), знайдений методом Ейлера, при 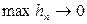 збігається до точного розв’язку рівномірно на обмеженому відрізку
збігається до точного розв’язку рівномірно на обмеженому відрізку 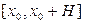 із сумарною похибкою
із сумарною похибкою  .
.
Отже, метод Ейлера має перший порядок точності.