Похибки заокруглень при розрахунках
При реалізації на ЕОМ алгоритмів, що містять велику кількість операцій множення і ділення, типовими є похибки округлення. При виконанні операцій множення кількість розрядів може зрости настільки, що всі вони вже не можуть бути розміщені в елементах запам'ятовуючих пристроїв ЕОМ. Частину розрядів праворуч доводиться відкидати, округляти числа. Сам по собі процес округлення числа не обов'язково призводить до внесення в нього якої-небудь істотної похибки. Так, при обчисленні зі звичайною точністю в сучасних ЕОМ можна утримувати, наприклад, дев'ять десяткових розрядів. Природно, щопростим відкиданням в ЕОМ десятого і наступних розрядів ми вносимо в число лише дуже незначні зміни. Порівняємо дванадцятирозрядне число 1000000,00297 і округлене дев’ятирозрядне число 1000000,00. Внесена в результаті округлення похибка становить величину 0,00297. Однак у процесі виконання великої кількості арифметичних операцій похибки, послідовно накопичуючись, породжують нові. Таке нагромадження похибок округлення може призвести до дуже істотних помилок в остаточних результатах.
Похибки округлення особливо доводиться враховувати при реалізації нестійких обчислювальних процесів, у яких незначні похибки у вихідних даних або результатах проміжних обчислень можуть призвести до істотних помилок у остаточному результаті.
Приклад. Нехай необхідно обчислити величину  за формулою
за формулою
 , (1.1)
, (1.1)
де а = 139,27; b = 138,97. Одержимо  = 0,3.
= 0,3.
Припустимо, що величини а і b обчислені з похибками, що не перевищують 1% їх точних значень, а=140,62, b=37,62. Обчислюючи величину  за формулою (1.1) із наближеними значеннями, одержимо с=140,62-137,62=3,0. Отже, похибки в обчисленні вихідних величин а і b призвели до десятикратного збільшення числа
за формулою (1.1) із наближеними значеннями, одержимо с=140,62-137,62=3,0. Отже, похибки в обчисленні вихідних величин а і b призвели до десятикратного збільшення числа  .
.
1.2 Абсолютна і відносна похибки
Абсолютна похибка - це модуль різниці між відповідним точним значенням розглянутої величини А і наближеним її значенням а. Вона має вигляд
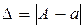 . (1.2)
. (1.2)
Безпосередньо за значенням абсолютної похибки досить важко робити висновок про ступінь розбіжності між точним значенням 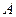 величини і його наближеним значенням. Так, похибка 2м цілком припустима при визначенні відстані між Києвом і Сумами та абсолютно неприпустима при вимірюванні розмірів кімнати. Тому застосовується ще одна характеристика наближених величин — їх відносна похибка.
величини і його наближеним значенням. Так, похибка 2м цілком припустима при визначенні відстані між Києвом і Сумами та абсолютно неприпустима при вимірюванні розмірів кімнати. Тому застосовується ще одна характеристика наближених величин — їх відносна похибка.
Відносною похибкою  наближеного значення величини, точне значення якої дорівнює А, називається відношення його абсолютної похибки
наближеного значення величини, точне значення якої дорівнює А, називається відношення його абсолютної похибки  до модуля точного значення, тобто
до модуля точного значення, тобто
 .(1.3)
.(1.3)
Наприклад, нехай в результаті вимірювання довжини бігової доріжки отримано значення а=99,1м. Точне значення цієї величини 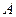 = 100м. Абсолютна похибка
= 100м. Абсолютна похибка 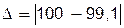 =0,9. Відносна похибка за формулою (1.3) становить
=0,9. Відносна похибка за формулою (1.3) становить 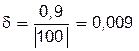 .
.
Із формул (1.2)—(1.3) бачимо, що абсолютна похибка має розмірність оцінюваних цією похибкою величин, відносна похибка завжди безрозмірна.
Величини  і
і  можуть бути обчислені точно лише в тих випадках, коли відоме не тільки наближене числове значення розглянутої величини, але і її точне значення. Останнє, однак, можливе далеко не у всіх випадках. Крім того, часто доводиться аналізувати похибки деякої множини наближених величин, наприклад, похибки вимірювання розмірів серії виготовлених деталей, викликані недосконалістю застосовуваних вимірювальних інструментів. Якість серії вимірювань для всіх деталей може оцінюватися найбільшою за модулем величиною абсолютної або відносної похибки їх розмірів. Тому часто вводяться поняття граничних абсолютної та відносної похибок.
можуть бути обчислені точно лише в тих випадках, коли відоме не тільки наближене числове значення розглянутої величини, але і її точне значення. Останнє, однак, можливе далеко не у всіх випадках. Крім того, часто доводиться аналізувати похибки деякої множини наближених величин, наприклад, похибки вимірювання розмірів серії виготовлених деталей, викликані недосконалістю застосовуваних вимірювальних інструментів. Якість серії вимірювань для всіх деталей може оцінюватися найбільшою за модулем величиною абсолютної або відносної похибки їх розмірів. Тому часто вводяться поняття граничних абсолютної та відносної похибок.
За граничну абсолютну похибку  * наближеного числа може бути взяте будь-яке число, не менше абсолютної похибки цього числа,
* наближеного числа може бути взяте будь-яке число, не менше абсолютної похибки цього числа,
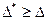 . (1.4)
. (1.4)
Аналогічно за граничну відносну похибку  * наближеного числа може бути взяте будь-яке число, що задовольняє умову
* наближеного числа може бути взяте будь-яке число, що задовольняє умову
 . (1.5)
. (1.5)
При аналізі серії вимірювань за  * і
* і  * беремо найбільші з отриманих відповідних значень
* беремо найбільші з отриманих відповідних значень  і
і  і тим самим визначаємо межі, всередині яких знаходяться відповідні похибки.
і тим самим визначаємо межі, всередині яких знаходяться відповідні похибки.
Значущими цифрами числа 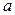 називають усі цифри в його записі, починаючи з першої ненульової зліва. Значущу цифру числа
називають усі цифри в його записі, починаючи з першої ненульової зліва. Значущу цифру числа 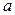 називають правильною, якщо абсолютна похибка числа не перевищує одиниці відповідного цій цифрі розряду.
називають правильною, якщо абсолютна похибка числа не перевищує одиниці відповідного цій цифрі розряду.
Приклад 1Для ряду 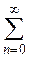
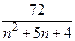 знайти суму S аналітично. Обчислити значення часткових сум ряду S
знайти суму S аналітично. Обчислити значення часткових сум ряду S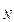 =
= і знайти величину похибки при значеннях
і знайти величину похибки при значеннях 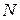 =
=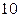 ,
, ,
,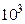 ,
,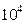 ,
, . Побудувати гістограму залежності правильних цифр результату від
. Побудувати гістограму залежності правильних цифр результату від 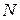 .
.
Знайдемо точну суму цього ряду:
S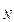 =
=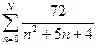 =
=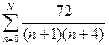 =
=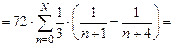
 ,
,
Отже, 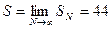 .Уведемо функцію часткових сум S(N)=
.Уведемо функцію часткових сум S(N)=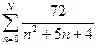 .. Тоді абсолютну похибку можна визначити за допомогою функції d(N) =
.. Тоді абсолютну похибку можна визначити за допомогою функції d(N) =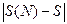 .
.
Результати обчислювального експерименту
| N N | Значення частк. суми ряду S(N) | Абсолютна похибка d(N) | Кільк. правил. цифр Mi |
| S(10)=38.439560439 | d(10) =5.56 | 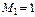
| |
| 1102 | S(100)=43.3009269 | d(100)=0.699 | 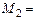 2 2
|
| 1103 | S(1000)=43.9282153 | d(1000)=0.072 | 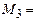 3 3
|
| 1104 | S(10000)=43.992802 | d(10000)=0.0072 |  4 4
|
| 1105 | S(100000)=43.99928021599 | d(100000)=0.00072 | 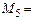 5 5
|
Висновок. Як бачимо з наведеного обчислювального експерименту, збільшення числа членів ряду в 10 разів порівняно з попереднім випадком збільшує число правильних цифр у відповіді на 1.
Гістограма
|

Приклад 2 Для матриці A=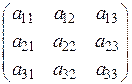 розв’язати питання про існування оберненої матриці в таких випадках:
розв’язати питання про існування оберненої матриці в таких випадках:
1) елементи матриці задані точно;
2) елементи матриці задані наближено з відносною похибкою a)  та b)
та b)  = b%. Знайти відносну похибку результату.
= b%. Знайти відносну похибку результату.
Це питання вирішується шляхом знаходження визначника й порівняння його з нулем. У випадку, коли елементи визначника задані точно, варто обчислити визначник і правильно відповісти на поставлене в задачі питання.
У випадку, коли елементи визначника задані наближено з відносною похибкою d, питання є складнішим. Нехай елементи матриці позначені через 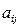 . Тоді кожен елемент матриці
. Тоді кожен елемент матриці 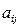 тепер уже не дорівнює конкретному значенню, а може набувати будь-якого значення з відрізка [
тепер уже не дорівнює конкретному значенню, а може набувати будь-якого значення з відрізка [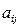 (1-d);
(1-d); 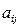 (1+d)], якщо
(1+d)], якщо 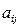 > 0 , і з відрізка [
> 0 , і з відрізка [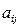 (1+d);
(1+d); 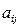 (1-d)], якщо
(1-d)], якщо 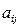 < 0. Множина всіх можливих значень елементів матриці являє собою замкнену обмежену множину в 9-вимірному просторі. Сам визначник є неперервною й диференційованою функцією 9 змінних - елементів матриці
< 0. Множина всіх можливих значень елементів матриці являє собою замкнену обмежену множину в 9-вимірному просторі. Сам визначник є неперервною й диференційованою функцією 9 змінних - елементів матриці 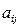 . За відомою теоремою Вейєрштрасса ця функція досягає на зазначеній множині свого найбільшого та найменшого значень M і m. Якщо відрізок [ m, M ] не містить точку 0 , то це означає, що при будь-яких припустимих значеннях елементів матриці
. За відомою теоремою Вейєрштрасса ця функція досягає на зазначеній множині свого найбільшого та найменшого значень M і m. Якщо відрізок [ m, M ] не містить точку 0 , то це означає, що при будь-яких припустимих значеннях елементів матриці 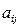 визначник не набуває значення 0. Якщо ж точка 0 належить відрізку [m, M], таке твердження буде неправомірним. Буде мати місце невизначеність.
визначник не набуває значення 0. Якщо ж точка 0 належить відрізку [m, M], таке твердження буде неправомірним. Буде мати місце невизначеність.
З’ясувати m і M допомагають наступні міркування. Як функція своїх аргументів (елементів матриці 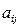 ) визначник має таку властивість (принцип максимуму): ця функція досягає свого найбільшого і найменшого значень завжди на границі області . Більше того, можна довести, що ці значення досягаються в точках, координати яких мають вигляд
) визначник має таку властивість (принцип максимуму): ця функція досягає свого найбільшого і найменшого значень завжди на границі області . Більше того, можна довести, що ці значення досягаються в точках, координати яких мають вигляд 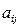 (1±d). Таких точок 2
(1±d). Таких точок 2 =512. У кожній з них варто обчислити визначник, а потім вибрати з отриманих значень найбільше та найменше. Це й будуть числа M і m.
=512. У кожній з них варто обчислити визначник, а потім вибрати з отриманих значень найбільше та найменше. Це й будуть числа M і m.
1.3 Середні квадратичні похибки
Нехай передбачається проведення серії вимірів деякої величини X. У кожному з вимірів буде отримане якесь її значення, причому залежно від точності приладу, зокрема, ці значення будуть знаходитися в деякому інтервалі, загальне їх число скінченне. Позначимо ці значення 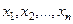 , їх ймовірності
, їх ймовірності  . Оскільки заздалегідь невідомо, яке значення величини Х буде отримано в кожному вимірі, ця величина є випадковою.
. Оскільки заздалегідь невідомо, яке значення величини Х буде отримано в кожному вимірі, ця величина є випадковою.
Математичне очікування Х виражається формулою
M[X]= . (1.6)
. (1.6)
Про якість вимірів, тобто ступінь розкиду помилок виміру, можна роб висновкиити за розмірами дисперсії, або середнього квадратичного відхилення випадкової величини:
D[X]=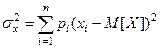 . (1.7)
. (1.7)
Величина 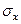 називається в теорії похибок середньою квадратичною похибкою вимірювання.
називається в теорії похибок середньою квадратичною похибкою вимірювання.
Якщо результати вимірювання є незалежними, тобто результат довільного виміру не залежить від того, які результати отримані в інших вимірах, для них прийнятні теореми Чебишева і Бернуллі. Зокрема, бувають наступні припущення.
1 Якщо випадкова величина Х набyває тільки невід’ємних значень, частина яких менша деякого додатного числа а, то
p[(X<a)]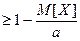 . (1.8)
. (1.8)
2 Якщо а > 0, то
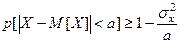 . (1.9)
. (1.9)
Відзначимо, що формулою (1.7) користуються для обчислення середніх квадратичних похибок і в детермінованих процесах
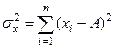
 , (1.10)
, (1.10)
де А —точне значення числа X, а  — абсолютні похибки.
— абсолютні похибки.
