Схеми Рунге-Кутта другого порядку
Невисокий ступінь точності методу Ейлера визначається перш за все тим, що залишковий член формули (8.4) 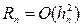 . Зажадаємо, щоб
. Зажадаємо, щоб 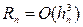 . За формулою Тейлора
. За формулою Тейлора
 ,
,
де залишковий член
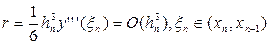 . (8.9)
. (8.9)
Рівність (8.9) справедлива, якщо у'’’(x) обмежена на 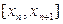 . З (8.1) випливає
. З (8.1) випливає
 .
.
Тут треба обчислювати частинні похідні функції f(x,y), що з причин, зазначених раніше, небажано. Щоб уникнути диференціювання, замінимо  виразом
виразом
 ,
,
де 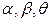 - деякі параметри. Тоді, якщо у формулі (8.9) відкинути залишок r , одержимо
- деякі параметри. Тоді, якщо у формулі (8.9) відкинути залишок r , одержимо
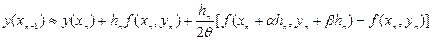 ,
,
або  , (8.10)
, (8.10)
де 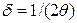 ;
;  .
.
Параметри  виберемо так, щоб розкладання точного розв’язку
виберемо так, щоб розкладання точного розв’язку  задачі (8.1)- (8.2) у вузлі
задачі (8.1)- (8.2) у вузлі 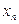 і його наближення
і його наближення  , що обчислюється за формулою (8.10), у ряди за степенями
, що обчислюється за формулою (8.10), у ряди за степенями 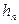 , збігалися з точністю до нескінченно малої найбільш високого порядку щодо
, збігалися з точністю до нескінченно малої найбільш високого порядку щодо 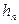 .
.
Для одержання точного розв’язку використовуємо формулу (8.9)
 ,
,
аналогічно для наближеного розв’язку
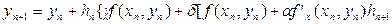 +
+

 .
.
Припускаючи, що  , і порівнюючи члени при однакових степенях
, і порівнюючи члени при однакових степенях 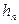 , одержимо
, одержимо 
Для визначення чотирьох невідомих параметрів маємо три рівняння. Виразимо  через інші параметри:
через інші параметри: 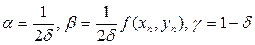 .
.
Підставляючи ці значення у (8.10), одержимо однопараметричне сімейство двочленних схем Рунге-Кутта:
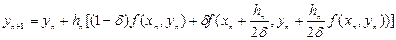 (8.11)
(8.11)
Відзначимо, що вибрати параметр  так, щоб збігалися коефіцієнти у формулі Тейлора при
так, щоб збігалися коефіцієнти у формулі Тейлора при 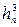 , неможливо.
, неможливо.
Формула (8.11) завдяки своїй досить великій точності широко використовується в чисельних розрахунках, при цьому найчастіше беруть або 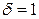 , або
, або  .
.
Підставляючи в (8.11) 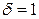 , одержимо розрахункову формулу
, одержимо розрахункову формулу
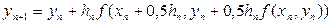 , (8.12)
, (8.12)
відому як формулу вдосконаленого методу Ейлера.
При використанні даного методу спочатку за формулою (8.5) обчислюємо наближене значення розв’язку при  . Після цього в знайденій точці визначаємо нахил інтегральної кривої:
. Після цього в знайденій точці визначаємо нахил інтегральної кривої:  , а потім знаходимо значення
, а потім знаходимо значення
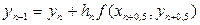 .
.
Покладаючи в (8.11)  =0,5, одержимо
=0,5, одержимо
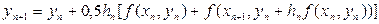 (8.13)
(8.13)
При використанні формули (8.13) спочатку обчислюється за методом Ейлера наближене значення 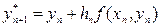 , потім нахил інтегральної кривої в новій точці
, потім нахил інтегральної кривої в новій точці 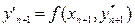 (рис. 8.4) Після цього визначається уточнене значення
(рис. 8.4) Після цього визначається уточнене значення 
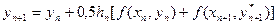 . (8.14)
. (8.14)
Розрахункова схема (8.13) або (8.14) називається методом Ейлера-Коші, або обчислювальним правилом типу предиктор-коректор.
Для схеми (8.14) можна довести, що якщо f(x,y) неперервна й обмежена разом зі своїми другими похідними, то розв’язок, отриманий за схемою (8.11) при будь-якому  і при
і при 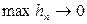 , рівномірно збігається до точного розв’язку із сумарною похибкою
, рівномірно збігається до точного розв’язку із сумарною похибкою 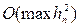 . Отже, схема (8.11) має другий порядок точності.
. Отже, схема (8.11) має другий порядок точності.