Метод Краута
Суть методу Краута, або LU-розкладання, полягає в тому, що це своєрідний перезапис методу Гауса. Він дозволяє зробити зручною комп’ютерну реалізацію методу Гауса. Можна явно виділити два етапи, у яких один робить перетворення з матрицею А системи, інший – з вектором правих частин b. Отже, нехай дана СЛАР Ax=b, наприклад, система розміром 4´4. Запишемо розширену матрицю системи

Тоді, за Гаусом можна явно виділити два етапи (тобто два кроки) – прямий хід (ПХ) і зворотний (ЗХ):
1) ПХ: 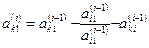
2) ЗХ: 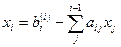
На прямому ході ми робимо так звані “виключення”, тобто приводимо матрицю до трикутного вигляду. Тепер легко знайти x4, а потім і x3 і т.д. Це був зворотний хід методу Гауса. Всі ці перетворення виконувалися не із самою матрицею, а з розширеною матрицею.
Головна ідея і потреба методу LU – декомпозиції полягає в тому, щоб розділити окремо етап перетворення коефіцієнтів матриці і окремо етап перетворення вектора правих частин.
Розглянемо  -ий крок методу Гауса, на якому здійснюється занулення піддіагональних елементів
-ий крок методу Гауса, на якому здійснюється занулення піддіагональних елементів  -го стовпчика матриці
-го стовпчика матриці 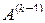 . Як було зазначено раніше, з цією метою використовується операція
. Як було зазначено раніше, з цією метою використовується операція


У термінах матричних операцій така операція еквівалентна множенню 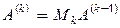 , де елементи матриці
, де елементи матриці 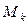 визначаються таким чином:
визначаються таким чином:
 тобто матриця
тобто матриця 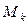 має
має 
вигляд  .
.
При цьому вираз для зворотної операції запишеться у вигляді  , де
, де
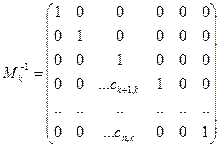 .
.
У результаті прямого ходу методу Гауса отримаємо 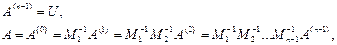
де 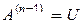 - верхня трикутна матриця, а
- верхня трикутна матриця, а  - нижня трикутна матриця, що має вигляд
- нижня трикутна матриця, що має вигляд
 .
.
У подальшому  - розкладання може бути ефективно використано для розв’язання систем лінійних алгебраїчних рівнянь. Це дозволяє один раз перетворити матрицю системи, а потім неодноразово розв’язувати декілька систем з різними правими частинами. Обчислювальні витрати при цьому будуть зводитися тільки до зворотного ходу.
- розкладання може бути ефективно використано для розв’язання систем лінійних алгебраїчних рівнянь. Це дозволяє один раз перетворити матрицю системи, а потім неодноразово розв’язувати декілька систем з різними правими частинами. Обчислювальні витрати при цьому будуть зводитися тільки до зворотного ходу.
Запишемо A×x= b, як
L×U×x= b.
Позначимо
U×x= y.
І , отже , L×y= b.
Таким чином, прямий хід методу LU-декомпозицiї складається з розкладу матриці A на нижню L та верхню U трикутні матриці – це прямий хiд.
Потiм визначається вектор y на основі співвідношень: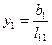 ,
, 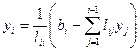 .
.
На зворотному ході методу LU-декомпозицiї розв’язується рівняння U×x= y. З урахуванням того, що U – трикутна матриця,

 ,
, .
.
Отже, LU-розкладання є просто свого роду іншою формою запису еквівалентних перетворень матриці за методом Гауса, але проведених з урахуванням умови А = L×U.
Теорема 1. Для існування LU-розкладання матриці А необхідно й достатньо, щоб у матриці А всі головні мінори були відмінні від нуля.
У довільної невиродженої матриці А головні мінори, тобто  ,
, 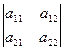 , …,
, …,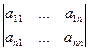 , можуть дорівнювати нулю. Тоді необхідно переставити рядки так, щоб головні мінори стали відмінними від нуля.
, можуть дорівнювати нулю. Тоді необхідно переставити рядки так, щоб головні мінори стали відмінними від нуля.
Звичайно перестановка рядків не проводиться окремо від процедури вилучення, ці два процеси поєднуються в один. Якщо a11=0, переставимо рядки матриці А так, щоб у лівому верхньому куті виявився ненульовий елемент. У першому стовпці такий елемент завжди знайдеться, інакше detА = 0. Якщо після першого кроку дістанемо a22(1) = 0, то виконаємо, як і вище, переставлення: у другому стовпці завжди знайдеться ненульовий елемент, інакше два перші стовпці були б лінійно залежні і det А = 0. Помістимо рядок з ненульовим елементом у другому стовпці на місце другого рядка, тоді a22(1)≠0. Продовжуючи цей процес вилучення й перестановки рядків (якщо елемент akk(k-1)=0) до k=n, дістанемо LU-розкладання матриці А з додатковою матрицею Р перестановок рядків
PA = LU.
Матриця Р одержується з одиничної матриці Е перестановкою тих самих рядків. Наприклад, перестановці другого та четвертого рядків матриці відповідає
P = 
Таким чином, ми отримали LUP-розкладання.
Приклад.Розв'яжемо СЛАР за схемою LU-розкладання:
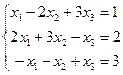
Виконаємо дії за алгоритмом і отримаємо матриці L та U у вигляді:
L=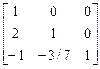 , U=
, U=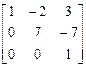 .
.
Спочатку знаходимо розв’язок системи 
 .
.
Отримаємо: g = {1, 0, 4}.
Тепер реалізуємо зворотний хід методу Гауса, розв’язуючи систему  :
:
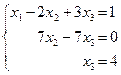 .
.
Отже, остаточна відповідь: x1 = 4, x2 = 4, x3 = -3.