Алгоритмы вывода линий

Многие современные программы (векторные графические редакторы, САПР, математические и другие специальные программы) работают с изобра­же­ниями, представленными некоторыми математическими моделями. Наиболее часто такие изображения составлены из стандартного набора простых элементов, называемых графическими примитивами. Это могут быть прямые и кривые линии, фигуры (прямоугольники, окружности, эллипсы) и т.п. Для того, чтобы такое изображение, состоящее из примитивов, достаточно перечислить эти примитивы, указать их параметры (цвет, толщину и стиль линий, способ заливки фигур и др.) и взаимное расположение.

Поскольку практически все современные средства отображения графики (дисплеи, принтеры) растровые, для отображения картинки, заданной в вектор­ном виде, необходимо преобразовать ее в растр. Такое преобразование обычно выполняется той программой, в которой изображение было создано, с исполь­зованием алгоритмов растеризации.

Для того, чтобы преобразовать в растр линию, необходимо изменить цвет пикселов, по которым эта линия проходит, рис. 13.2 а. Чтобы это сделать, нужно получить уравнение линии. Очевидно, наиболее простым графическим прими­тивом является отрезок прямой, который может быть задан координатами двух точек: начала (x₁, y₁) и конца — (x₂, y₂). Для произвольной точки (x, y), лежащей на отрезке прямой, должно выполняться условие

. (13.12)

Отсюда можем получить уравнение прямой как функцию y от x или наоборот:

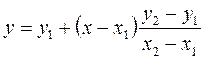. (13.13)

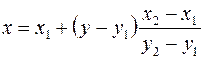. (13.14)

Очевидно, что дробь в уравнении представляет собой угловой коэффи­ци­ент и при построении может быть вычислена один раз. Для растеризации отрезка следует выяснить, какая из величин dx = x₂ – x₁ и dy = y₂ – y₁ больше, и построить «график» функции y = f₁ (x) в первом или x = f₁ (y) во втором случае. Выполняется простой цикл по соответствующей координаты от начальной до конечной точки с шагом в один пиксел. Другая координата определяется расчетом по (13.13) или (13.14) и округляется до целого значения; пиксел с полученными координатами (x, y) закрашивается заданным цветом.

Для точек окружности выполняется уравнение

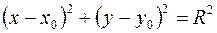, (13.15)

где R – радиус окружности, а (x₀, y₀) – координаты ее центра, рис. 13.2 б. Преобразовав это выражение, получим зависимость

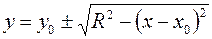, (13.16)

Поскольку окружность симметрична относительно вертикальной и горизон­таль­ной осей, проходящих через ее центр, необязательно рассчитывать все точки окружности. Достаточно выполнить расчет для дуги 1-2 — октанта (1/8) окружности, — для чего выполняется цикл по координате x от x₀ до x₁ с шагом в один пиксел и вычисляются и округляются до целого соответствующие значения у. Затем закрашивается пиксел A(x, y) и еще семь пикселов, расположенных на дугах 2-3, 3-4, …, 8-1.

Для построения эллипса существует два способа. Первый — аналогич­ный вышеописанному, при этом используется уравнение эллипса

, (13.17)

где a и b – половины длин осей эллипса. Расчет выполняется не для октанта, а для всего квадранта, остальные 3 квадранта строятся симметрично.

Второй способ — использование алгоритма построения окружности с последующим масштабированием — «растягиванием» окружности пропорци­о­нально длинам осей эллипса.

Описанные выше способы построения линий просты для понимания, но их реализация связана с использованием операций с плавающей точкой, умножения и деления, извлечения квадратного корня. Такие операции выполня­ются процессором относительно медленно, что приводит к низкой скорости отображения, особенно на маломощных ЭВМ.

Существуют инкрементные алгоритмы растеризации, называемые еще алгоритмами Брезенхэма, позволяющие строить отрезки прямых, окружностей, эллипсов и других кривых, используя только операции целочисленного сложе­ния и вычитания. Сущность алгоритма Брезенхэма проиллюстрируем на примере построе­ния отрезка, рис. 13.3:

1. Определяем величины приращений: dx = x₂ – x₁; dy = y₂ – y₁.

2. Выбираем большее из приращений: dx > dy, значит d = dx.

3. Вводим текущие координаты x и y, а также вспомогательные пере­менные ex и ey. До начала цикла принимаем x = x₁; y = y₁; ex = 0; ey = 0. Закрашиваем пиксел с координатами (x, y)

4. Выполняем d раз цикл, в котором переменные ex и ey увеличиваем соответственно на dx и dy. Поле координат (ex, ey) условно разобьем на квадраты со стороной d. При выходе точки (ex, ey) за границу текущего квадра­та по горизонтали или по вертикали значение соответственно x или y изменя­ется (увеличивается или уменьшается, в зависимости от направления отрезка) на 1. Получаем координаты следующего пиксела. Закрашиваем пиксел.

Анало­гичные, но несколько более сложные алгоритмы используются для построения окруж­ностей, эллипсов, дуг. Как видно, в приведенном алгоритме используются только операции сло­жения, вычитания и сравнения. Поскольку последние выполняются во много раз быстрее операций с плава­ющей точкой, такие алгоритмы обеспечивают высокую скорость отображения даже на маломощных ЭВМ.

К недостаткам алгоритма можно отнести некоторую «неточность» засвет­ки пикселов, что видно из рис. 13.3, а также то, что опорные точки отрезков и других фигур могут иметь лишь целочисленные координаты (середины соот­вет­ствующих пикселов).