Дифракционные формулы Френеля и Фраунгофера
Рассмотрим дифракцию света, падающего на непрозрачный экран с отверстием произвольной формы. Отверстие в экране называют апертурой. В зависимости от удаленности источника света и плоскости наблюдения от дифрагирующего экрана различают зоны дифракции Фраунгофера и Френеля. Дифракция Фраунгофера наблюдается в дальней зоне, удаленной от дифрагирующего экрана на расстояние, во много раз превышающее размеры апертуры. Дифракция Френеля имеет место в ближней зоне, распространяющейся до зоны дифракции Фраунгофера. Дифракция Фраунгофера по существу является предельным случаем дифракции Френеля при больших расстояниях от экрана. Заметим, что зона дифракции Френеля также начинается на некотором расстоянии от экрана. Непосредственно за апертурой в близи экрана находится область тени . Здесь и далее будем предполагать, что размеры отверстия на экране велики по сравнению с длиной волны падающего света, а источник света находится на таком расстоянии от экрана, что свет, падающий на экран, имеет практически плоский волновой фронт и постоянную амплитуду.
В общем случае апертура представляет собой транспарант с двумерной амплитудной функцией пропускания. В частном случае апертура является отверстием с амплитудной функцией пропускания
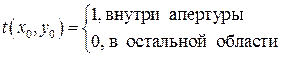 (24)
(24)
Данный случай важен, поскольку часто встречается при анализе оптических систем хранения и обработки информации [3,4]. В любом из рассмотренных случаев непосредственно за экраном при z= +0 световое поле описывается распределением амплитуд
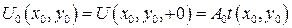 (25).
(25).
 Свет, падающий на экран, также имеет произвольную комплексную амплитуду U(x,y,-0). Тогда световое поле имеет за экраном комплексную амплитуду:
Свет, падающий на экран, также имеет произвольную комплексную амплитуду U(x,y,-0). Тогда световое поле имеет за экраном комплексную амплитуду:  (26)
(26)
В дальнейшем будем считать, что непосредственно за экраном световое поле имеет комплексную амплитуду U(x0,y0). Поэтому интеграл Френеля Кирхгофа (23) можно записать в виде
 , (27)
, (27)
где 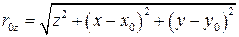
Приближение Френеля. Для дифракционного поля в области, удаленной от экрана на расстояние, значительно превышающее максимальный размер апертуры, интеграл Френеля Кирхгофа (27) значительно упростится. Действительно, если
 (28),
(28),
то можно полагать, что cosqzr»1 ошибкой менее 5%, если угол qzr <18°. Расстояние r0z в знаменателе подынтегрального выражения (27) можно заменить координатой z, поскольку
 (29)
(29)
и (x-x0)2/z2»0, (y-y0)2/z2»0 (согласно (28). Однако выражение (29) неприемлемо для замены r0z, в экспоненциальном члене, так как на экспоненту влияет даже малое изменение r0z. Для получения более точного приближения воспользуемся разложением 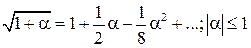 . Учитывая первые два члена данного разложения для аппроксимации квадратного корня, примем
. Учитывая первые два члена данного разложения для аппроксимации квадратного корня, примем 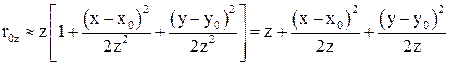 (30)
(30)
С учетом (28) - (30) интеграл Френеля-Кирхгофа можно записать в следующем упрощенном виде: 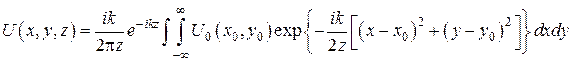 (31)
(31)
Данное выражение называют приближением Френеля, а соответствующее ему поле дифракционных полем Френеля. Интегральное преобразование вида
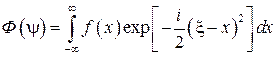 (32)
(32)
где 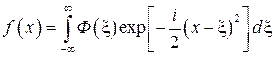 (33)
(33)
называют преобразованием Френеля. Следовательно, приближение Френеля (31) представляет собой двумерное преобразование Френеля дифрагировавшего на экране светового поля. Приближение Френеля справедливо в зоне [3]
 (34)
(34)
где a- максимальный радиус апертуры; r- максимальный радиус области наблюдения в плоскости z , lmin- наименьшая неоднородность распределения светового поля U0 (x0,y0)), связанная с максимальной пространственной частотой поля nmax=2p¤lmin.
Приближение Фраунгофера. Ранее отмечалось, что дифракция Фраунгофера является предельным случаем дифракции Френеля при больших значениях z, т. е. в дальней зоне. При этом можно принять более жесткое допущение, нежели чем (28), а именно
 . (35)
. (35)
Рассмотрим приближение Френеля, записанное ввиде (33). С учетом допущения (35) можно принять exp[-i . Тогда дифракционная формула (33) еще более упростится
. Тогда дифракционная формула (33) еще более упростится
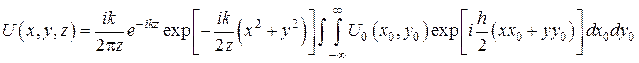 (36)
(36)
Полученное приближение имеет основной множитель в виде интеграла, являющегося преобразованием Фурье распределения комплексных амплитуд U0(х0,у0,) света, дифрагировавшего на экране, и его называют приближением Фраунгофера.
Таким образом, дифракция Фраунгофера представляет собой фурье-образ светового поля, дифрагировавшего на экране, умноженный на квадратичный фазовый множитель  . Если интересующая область в плоскости наблюдения дифракции Фраунгофера лежит вблизи оси z, так что выполняется условие
. Если интересующая область в плоскости наблюдения дифракции Фраунгофера лежит вблизи оси z, так что выполняется условие
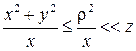 (37)
(37)
или  ,то
,то  .
.
В последнем случае приближение Фраунгофера упрощается:
 (38)
(38)
Зона дифракции Фраунгофера определяется из условия
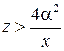 (39)
(39)
Если a=100 мкм; l=0,63 мкм, то зоне дифракции Фраунгофера соответствует условие z> 6,35 см.
Приближение тени. Если требуется определить поле вблизи экрана, то используют приближение тени:
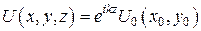 (40)
(40)
справедливое при [3]
 . (41)
. (41)