Оптические системы, выполняющие преобразование Фурье.
С помощью простой сферической линзы можно создавать картину, являющуюся фурье-образом входного изображения. Благодаря этому свойству, а также возможности применения линз для формирования световых пучков требуемой конфигурации они находят широкое применение в оптических системах хранения и обработки информации.
Рассмотрим простейшую оптическую систему (рис.6), состоящую из одной тонкой сферической линзы с фокусным расстоянием f, помещенной в плоскости z = 0, и расположенного вплотную к ней транспаранта с комплексным амплитудным пропусканием t (x0,y0). Линзу называют тонкой, если луч, входящий в точку с координатами (х0,у0), выходит из нее на противоположной поверхности в точке примерно с теми же координатами. Это означает, что смещением луча внутри линзы можно пренебречь; линза задерживает фронт падающей волны на значение, пропорциональное толщине линзы в каждой точке. Следовательно, тонкую линзу можно рассматривать как транспарант, осуществляю
Рис. 6. Схема оптической системы, выполняющей преобразование Фурье
щий фазовую модуляцию и имеющий функцию пропускания вида tl(x,y)=exp[iDj(x,y)], где функция Dj(x,y пропорциональна толщине линзы в точке с координатами (х, у). Нетрудно показать [4], что
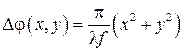(42)
Таким образом, соответствующее тонкой сферической линзе комплексное пропускание
.(43)
Допустим, что на рассматриваемую оптическую систему (рис.6) падает плоская волна амплитудой А0, распространяющаяся в положительном направлении оси z. Комплексная амплитуда света непосредственно вблизи линзы справа от нее равна произведению функции пропускания транспаранта и линзы:
(44)
Далее волна распространяется в свободном пространстве, поэтому комплексная амплитуда света на любом расстоянии от линзы может быть рассчитана с помощью интеграла Френеля Кирхгофа (27).. Для расчета распределения комплексных амплитуд света на расстоянии z =d от линзы воспользуемся приближением Френеля (31).
(45)
Интегрирование производят по всей поверхности линзьг. Подставим в (45) выражение (44), опустив несущественный для дальнейшего анализа постоянный фазовый множитель exp(-ikd),
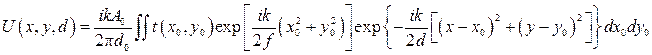(46)
Тогда после упрощения, если d = f, т. е. рассматривается распределение комплексных амплитуд света в задней фокальной плоскости линзы, выражение (46) еще более упрощается и принимает следующий вид: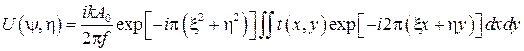 
, (47)
где
(48)
Интеграл в данном выражении представляет собой двумерное преобразование Фурье функции t (х,y) при условии, что функция t (х, у) тождественно равна нулю за пределами поверхности линзы. Это условие позволяет расширить пределы интегрирования до бесконечности, что и требуется для преобразования Фурье Таким образом, если на тонкую сферическую линзу с примыкающим к ней транспарантом падает плоская световая волна, то в задней фокальной плоскости линзы образуется световое, поле с распределением комплексных амплитуд, пропорциональным произведению квадратичного фазового множителя и фурье-образа функции пропускания транспаранта. В тех случаях, когда важна только интенсивность света, квадратичный фазовый множитель в выражении (47) не учитывают. Эффект, обусловленный этим множителем, эквивалентен действию тонкой рассеивающей (вогнутой) линзы с фокусным расстоянием f, помещенной в плоскости z=f. Если в плоскости z=f поместить тонкую собирающую линзу с фокусным расстоянием f, то этот фазовый множитель будет компенсирован. В результате получают оптическую систему (рис. 7), выполняющую точное преобразование Фурье
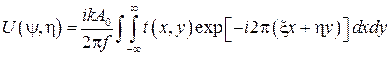(49)
Предполагается, что за пределами поверхности транспаранта t(x,y)º0. Если линза имеет неограниченные размеры, а транспарант совершенно прозрачен, т. е, t(x,y)=1,то
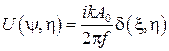(50)
Следовательно, падающая на линзу плоская световая волна фокусируется в точку на задней фокальной плоскости линзы. Линза конечных размеров образует световое пятно малых, но все же конечных размеров, что и наблюдается на практике.
Рис. 7. Оптическая схема, выполняющая точное преобразование Фурье