Дискретное преобразование Фурье.

Рассмотрим одномерное преобразование Фурье. Фурье-образ одномерной функции

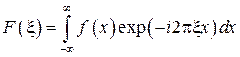(75)

При анализе оптических сигналов с помощью ЭВМ, как правило, вместо непрерывных сигналов располагают набором их дискретных значений (отсчетов). Пусть функция f(x,y) имеет ограниченный спектр в интервале -x_max и x_max и задана отсчетами в последовательных точках, которые отстоят друг от друга на расстоянии Dx = 0.5x^-1_max. Тогда, согласно теореме отсчетов (74), эта функция может быть представлена в виде следующего ряда:

(76)

Проанализируем получаемую форму фурье-образа F(x), для чего выражение (76) подставим в (75). В результате получим

(77)

Выражение (77) определяет фурье-образ исходной функции, заданной дискретными отсчетами. Действительно из (77) следует, что в интервале -x_max £x £ x_max

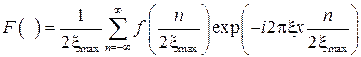(78)

для всех остальных значений x F(x) =0.

Допустим, что функция f(x) имеет не только ограниченный спектр, но и сама ограничена интервалом -x_max£ x £.x_max. Такое допущение неверно, так как функция, имеющая ограниченный спектр, не может одновременно быть ограниченной в пространстве. Однако при больших значениях произведения x_maxx_max погрешность, возникающая из-за этого допущения при вычислении фурье-образа функции, оказывается пренебрежимо малой. Таким образом, можно считать, что f(x) oграничена в пространстве интервалом [-x_max, x_max]. Тогда из теоремы отсчетов следует, что спектр F(x) функции f(x) может быть восстановлен по отсчетам, взятым с шагом Dx = 1/(2x_max), с помощью соотношения, аналогичного (76). Следовательно, достаточно вычислить значения фурье-образа в выборочных точках, что позволяет сократить объемы необходимой памяти и машинного времени, для расчета и хранения спектра сигнала. Подставив в (78) вместо аргумента x его дискретные значения в точках выборки x_n = nDx = n/(2x_max), получим выражение

(79)

 

называемое дискретным преобразованием Фурье, которое определяет значения отсчетов фурье-образа F(x).

Число отсчетов функции f(x) в интервале -x_max£ x £.x_max M=2x_max/(Dx)=4x_maxx_max. Аналогично число дискретных отсчетов фурье-образа в интервале частот -x_max £x £ x_max N = (2x_max)/(Dx)=4x_maxx_max.

Следовательно, M =N =4x_max x_max т е. для исходной функции f(x), как и для ее Фурье-образа. требуются одинаковые объемы выборки.

Таким же образом можно найти двумерное дискретное преобразование

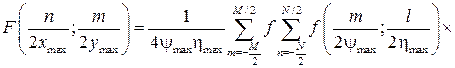
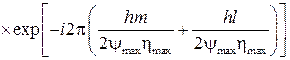(80)

Дадим математическое определение дискретного преобразования Фурье. Пусть функция f(x) задана последовательностью значений f_o,f₁,…,f_N-1 в N равноотстоящих друг от друга точках числовой прямой. Дискретным преобразованием Фурье (ДПФ) этой последовательности называют последовательность F₀, F₁,…F_N-1 определяемую суммой вида

(81)

ДПФ обладает свойством обратимости, т. е

(82)

 

Выражения (81) и (82) представляют одномерные ДПФ: первое характеризует прямое ДПФ, второе обратное ДПФ. Они отличаются знаком экспоненты.

Аналогичным образом определяются двумерные ДПФ. При этом двумерная функция f(x,y) задается матрицей выборочных значений f(n,m) (n=0,1,2,…N-1; m = 0,1,2,…M-1). Двумерное преобразование также обратимо Для вычисления даже при небольших значениях N и М потребуется большое количество машинного времени. Например, чтобы рассчитать ДПФ матрицы, необходимо около 6 ч машинного времени на ЭВМ, имеющей быстродействие около 10⁶ оп/с. Поэтому ДПФ приобрело практическое значение только после изобретения так называемых быстрых алгоритмов (БПФ). Один из таких алгоритмов позволил сократить число операций в, М раз (М = N). Для нашего случая (М = N = 1024) при использовании БПФ число операций сократится примерно в 100 раз, что приведет к снижению затрат машинного времени приблизительно до 4 мин. В настоящее время существует множество вариантов быстрых алгоритмов вычисления ДПФ.