Функции нескольких переменных
Частной производной от функции 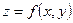 по независимой переменной
по независимой переменной 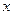 называется предел отношения частного приращения
называется предел отношения частного приращения 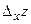 по
по 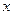 к приращению
к приращению 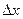 при стремлении
при стремлении 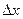 к нулю, т.е.
к нулю, т.е.
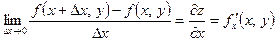 , (2.1)
, (2.1)
вычисленный при постоянном 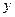 .
.
Частной производной от функции 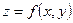 по независимой переменной
по независимой переменной 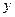 называется предел отношения частного приращения
называется предел отношения частного приращения 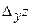 по
по 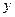 к приращению
к приращению 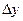 при стремлении
при стремлении 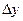 к нулю, т.е.
к нулю, т.е.
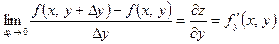 , (2.2)
, (2.2)
вычисленный при постоянном 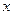 .
.
В общем случае, частная производная функции нескольких переменных определяется как производная функции одной из этих переменных при условии постоянства значений остальных независимых переменных. Поэтому частные производные функции нескольких переменных 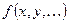 находят по формулам и правилам вычисления производных функции одной переменной.
находят по формулам и правилам вычисления производных функции одной переменной.
Пример 2.1. Найти частные производные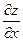 и
и 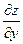 , если
, если 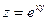 .
.
Решение. 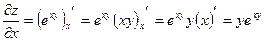 ,
,
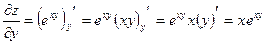 .
.
Пример 2.2. Найти частные производные 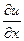 ,
, 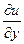 и
и 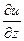 , если
, если 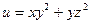 .
.
Решение. 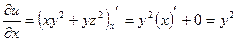 ,
,
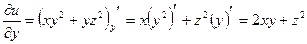 ,
,
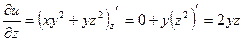 .
.
Полным приращением функции 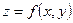 в точке
в точке 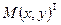 называется разность
называется разность 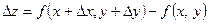 , где
, где 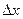 и
и 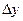 – произвольные приращения аргументов.
– произвольные приращения аргументов.
Функция 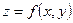 называется дифференцируемой в точке
называется дифференцируемой в точке 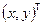 , если в этой точке полное приращение можно представить в виде
, если в этой точке полное приращение можно представить в виде
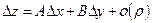 , (2.3)
, (2.3)
где 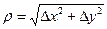 ,
, 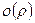 – бесконечно малая величина при
– бесконечно малая величина при 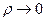 , А и В – постоянные.
, А и В – постоянные.
Полным дифференциалом функции 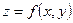 называется главная часть полного приращения
называется главная часть полного приращения 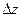 , линейная относительно приращений аргументов
, линейная относительно приращений аргументов 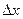 и
и 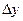 , т.е.
, т.е. 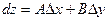 .
.
Дифференциалы независимых переменных совпадают с их приращениями, т.е. 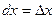 и
и 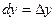 .
.
Полный дифференциал 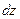 функции двух аргументов
функции двух аргументов 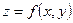 находится вычисляется по формуле
находится вычисляется по формуле
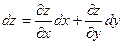 . (2.4)
. (2.4)
Аналогично, полный дифференциал 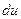 функции трех аргументов
функции трех аргументов 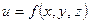 вычисляется по формуле
вычисляется по формуле
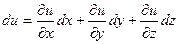 . (2.5)
. (2.5)
Пример 2.3. Найти полный дифференциал 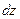 , если функция
, если функция 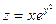 .
.
Решение. Найдем частные производные: 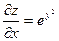 ,
, 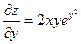 .
.
Тогда полный дифференциал принимает вид: 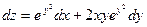 .
.
Для дифференцируемой функции 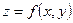 при достаточно малом
при достаточно малом 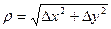 , если
, если 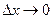 и
и 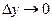 , справедливо приближенное равенство
, справедливо приближенное равенство
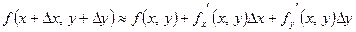 . (2.6)
. (2.6)
Формула (2.6) используется в приближенных расчетах.
Пример 2.4. Вычислить приближенно 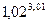 .
.
Решение. Рассмотрим функцию 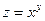 . Тогда
. Тогда 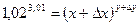 ,
,
где 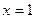 ,
, 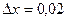 ,
, 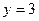 ,
, 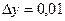 .
.
Вычислим частные производные: 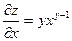 ,
, 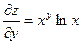 .
.
По формуле (2.6) получим: 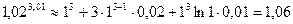 .
.