рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Образование
- /
- В.А. Дегтярева
Реферат Курсовая Конспект
В.А. Дегтярева
В.А. Дегтярева - раздел Образование, Федеральное Агентство По Образованию Государственное...
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
Государственное образовательное учреждение высшего профессионального
образования
«Ковровская государственная технологическая академия имени
В.А. Дегтярева»
ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
Учебно-методическое пособие Е.А. МироноваСОДЕРЖАНИЕ
| Введение.……………………………………………………………………… | |
| § 1. Понятие функции двух переменных………………................................ | |
| § 2.Частные производные и дифференциалы функции нескольких переменных……………………………………………………………… | |
| § 3. Производная сложной и неявной функции……………………………. | |
| § 4. Касательная плоскость и нормаль к поверхности…………………….. | |
| § 5. Производная по направлению. Градиент. Линеаризация…………….. | |
| § 6. Частные производные и дифференциалы высших порядков………… | |
| § 7. Экстремум функции двух переменных………………………………… | |
| § 8. Наибольшее и наименьшее значение функции двух переменных в замкнутой области…………………………………………………………… | |
| Задания для самостоятельной работы студентов.………………………….. | |
| Пример выполнения заданий самостоятельной работы студентов ….…… | |
| Приложение….…………….…………………………………………………. | |
| Литература………………….………………………………………………… |
ВВЕДЕНИЕ
Настоящее учебно-методическое пособие включает в себя краткие теоретические сведения из раздела «Функции нескольких переменных», задания для самостоятельной работы студентов и пример выполнения одного варианта заданий. В конце пособия приведён список литературы.
Содержание пособия подчинено требованиям современного государственного образовательного стандарта по математике для студентов технических и экономических специальностей. Краткие теоретические сведения, изложенные в пособии, даны в объёме достаточном для решения заданий самостоятельной работы студентов. Сами задания СРС содержат условия 10 задач (30 вариантов). Приложение содержит примеры нахождения частных производных с использованием системы MathCad. Материалы пособия предназначены для студентов, изучающих раздел «Функции нескольких переменных» и будут полезны преподавателям для составления заданий СРС.
Понятие функции двух переменных
Соответствие , которое каждой паре чисел сопоставляет одно и только одно число , называется функцией двух переменных, определенной на множестве со… Символически функция двух переменных обозначается так: или . (1.1)Частные производные и дифференциалы
Функции нескольких переменных
, (2.1) вычисленный при постоянном . Частной производной от функции по независимой переменной называется предел отношения частного приращения по к…Производная сложной и неявной функции
Если – дифференцируемая в точке функция, а аргументы и – дифференцируемые функции независимой переменной , т.е. и, то производная сложной функции… (3.1). Если переменная совпадает с одним из аргументов или , например , то производная сложной функции одной переменной…Касательная плоскость и нормаль к поверхности
Нормалью к поверхности в точке называется прямая, проходящая через точку перпендикулярно касательной плоскости в этой точке. Если поверхность задана явно функцией и в точке существуют конечные частные… , (4.1)Производная по направлению. Градиент. Линеаризация
, где . (5.1) Если функция дифференцируема, то производная по направлению вектора находится… , (5.2)Частные производные и дифференциалы высших порядков
Обозначения частных производных второго порядка ; ; ; .Экстремум функции двух переменных
Точка называется точкой минимума функции , если существует такая - окрестность точки , что для каждой точки , отличной от точки из этой окрестности,… Значение функции в точке максимума (минимума) называется максимумом… Если дифференцируемая функция имеет экстремум в точке , то ее частные производные в этой точке равны нулю, т.е.Наибольшее и наименьшее значение функции нескольких
Переменных в замкнутой области
Для того чтобы найти наибольшее и наименьшее значения функции в замкнутой области, надо: 1) найти стационарные точки, расположенные в данной области, и вычислить… 2) найти наибольшее и наименьшее значения функции на линиях, образующих границу области;Задания для самостоятельной работы студентов
Задание№1.
 |
Найти и изобразить область определения функции нескольких переменных
 |
.
1. а) 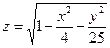 б)
б) 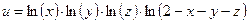
2. а) 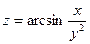 б)
б) 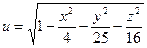
3. а) 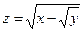 б)
б) 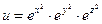
4. а) 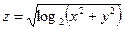 б)
б) 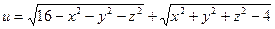
5. а) 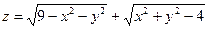 б)
б) 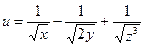
6. а) 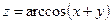 б)
б) 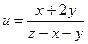
7. а) 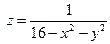 б)
б) 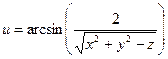
8. а) 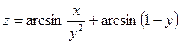 б)
б) 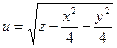
9. а) 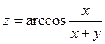 б)
б) 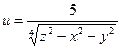
10. а) 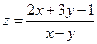 б)
б) 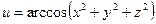
11. а) 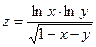 б)
б) 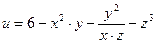
12. а) 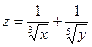 б)
б) 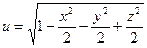
13. а) 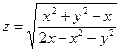 б)
б) 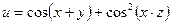
14. а) 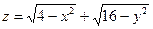 б)
б) 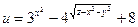
15. а) 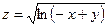 б)
б) 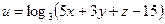
16. а) 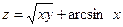 б)
б) 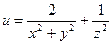
17. а) 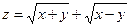 б)
б) 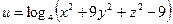
18. а) 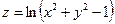 б)
б) 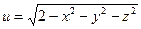
19. а)  б)
б) 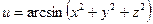
20. а) 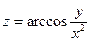 б)
б) 
21. а) 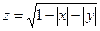 б)
б) 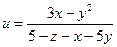
22. а) 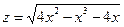 б)
б) 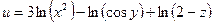
23. а) 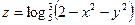 б)
б) 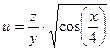
24. а) 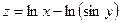 б)
б) 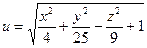
25. а) 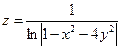 б)
б) 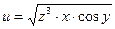
26. а) 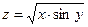 б)
б) 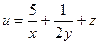
27. а) 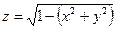 б)
б) 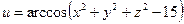
28. а) 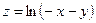 б)
б) 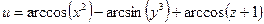
29. а) 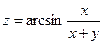 б)
б) 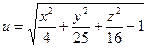
30. а) 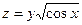 б)
б) 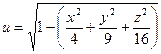
Задание №2.
Найти дифференциалы первого и второго порядков функция нескольких переменных.
1. а) 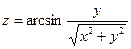 б)
б) 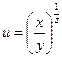
2. а) 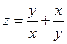 б)
б) 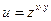
3. а) 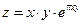 б)
б) 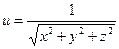
4. а) 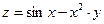 б)
б) 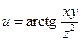
5. а) 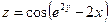 б)
б) 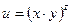
6. а) 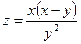 б)
б) 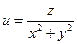
7. а) 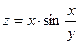 б)
б) 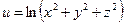
8. а) 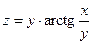 б)
б) 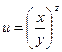
9. а) 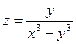 б)
б) 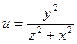
10. а) 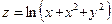 б)
б) 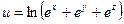
11. а) 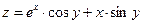 б)
б) 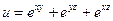
12. а) 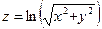 б)
б) 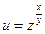
13. а) 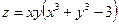 б)
б) 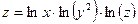
14. а) 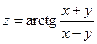 б)
б) 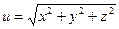
15. а) 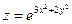 б)
б) 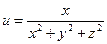
16. а) 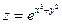 б)
б) 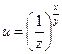
17. а) 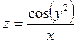 б)
б) 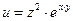
18. а) 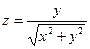 б)
б) 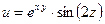
19. а) 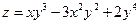 б)
б) 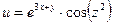
20. а) 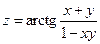 б)
б) 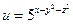
21. а) 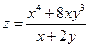 б)
б) 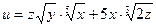
22. а) 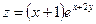 б)
б) 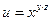
23. а) 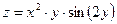 б)
б) 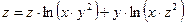
24. а) 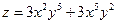 б)
б) 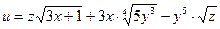
25. а) 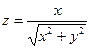 б)
б) 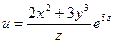
26. а) 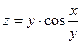 б)
б) 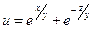
27. а) 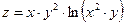 б)
б) 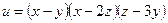
28. а) 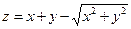 б)
б) 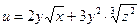
29. а) 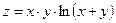 б)
б) 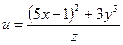
30. а) 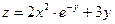 б)
б) 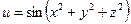
Задание№3.
Вычислить приближенно (считая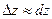 ).
).
Задание№4.
Дана сложная функция. Найти
а) 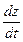 , если
, если 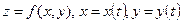 ;
;
б) 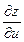 и
и 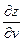 , если
, если 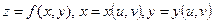 .
.
1. а) 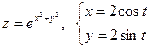 б)
б) 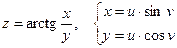
2. а) 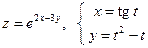 б)
б) 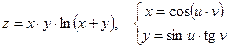
3. а) 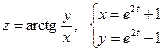 б)
б) 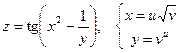
4. а) 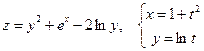 б)
б) 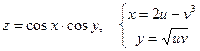
5. а) 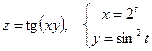 б)
б) 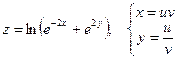
6. а) 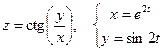 б)
б) 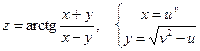
7. а) 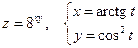 б)
б) 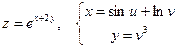
8. а) 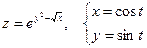 б)
б) 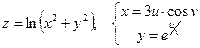
9. а) 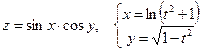 б)
б) 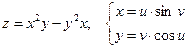
10. а) 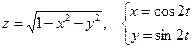 б)
б) 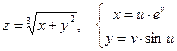
11. а) 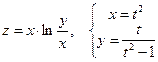 б)
б) 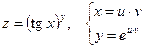
12. а) 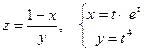 б)
б) 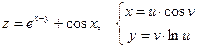
13. а) 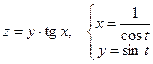 б)
б) 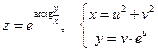
14. а) 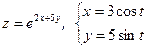 б)
б) 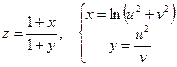
15. а) 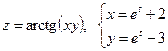 б)
б) 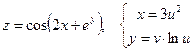
16. а) 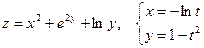 б)
б) 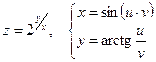
17. а) 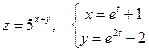 б)
б) 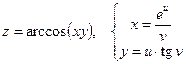
18. а) 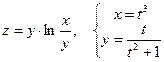 б)
б) 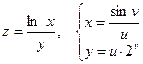
19. а) 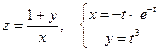 б)
б) 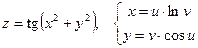
20. а) 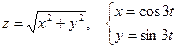 б)
б) 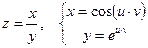
21. а) 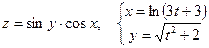 б)
б) 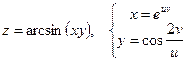
22. а) 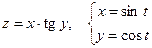 б)
б) 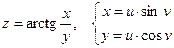
23. а) 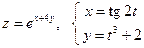 б)
б) 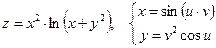
24. а) 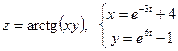 б)
б) 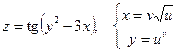
25. а) 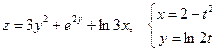 б)
б) 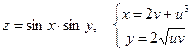
26. а) 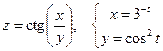 б)
б) 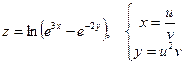
27. а) 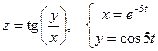 б)
б) 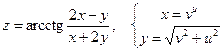
28. а) 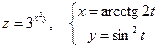 б)
б) 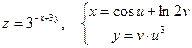
29. а) 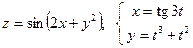 б)
б) 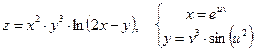
30. а) 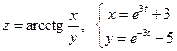 б)
б) 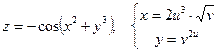

Задание№5.
Показать, что данная функция удовлетворяет уравнению.
1. а) 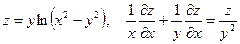
б) 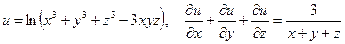
2. а) 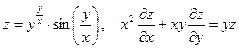
б) 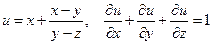
3. а) 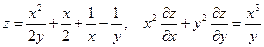
б) 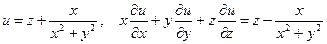
4. а) 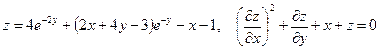
б) 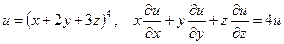
5. а) 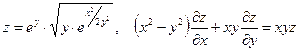
б) 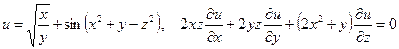
6. а) 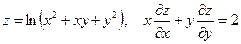
б) 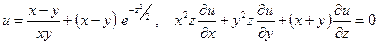
7. а) 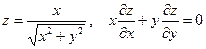
б) 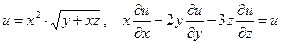
8. а) 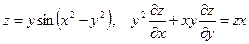
б) 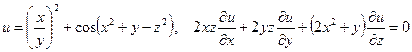
9. а) 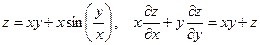
б) 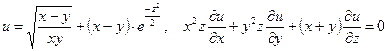
10. а) 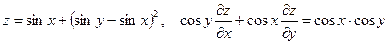
б) 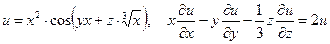
11. а) 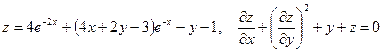
б) 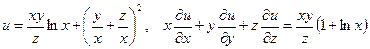
12. а) 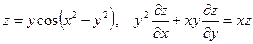
б) 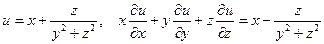
13. а) 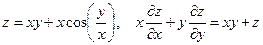
б) 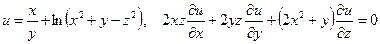
14. а) 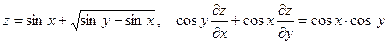
б) 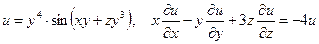
15. а) 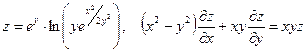
б) 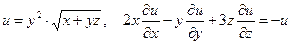
16. а) 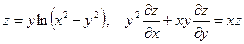
б) 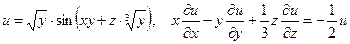
17. а) 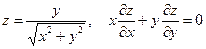
б) 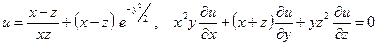
18. а) 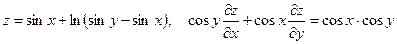
б) 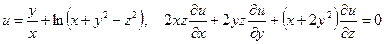
19. а) 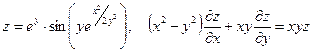
б) 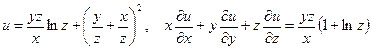
20. а) 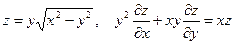
б) 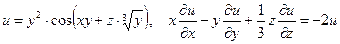
21. а) 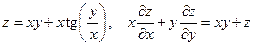
б) 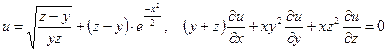
22. а) 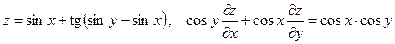
б) 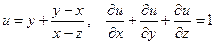
23. а) 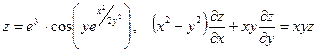
б) 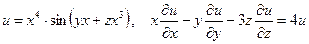
24. а) 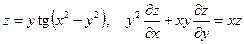
б) 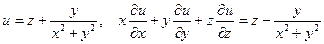
25. а) 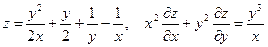
б) 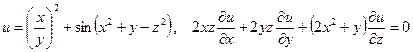
26. а) 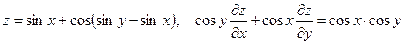
б) 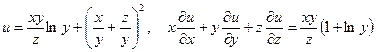
27. а) 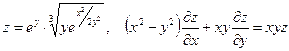
б) 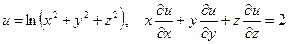
28. а) 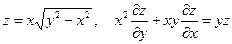
б) 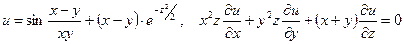
29. а) 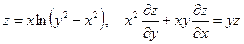
б) 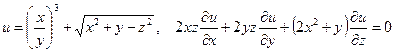
30. а) 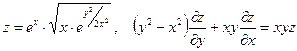
б) 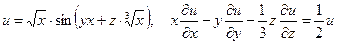
Задание №6.
Найти
а) полную производную 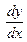 ;
;
б) частные производные 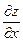 и
и 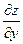
от неявной функции заданной уравнением:
1. а) 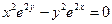 б)
б) 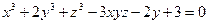
2. а) 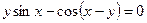 б)
б) 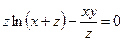
3. а) 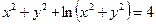 б)
б) 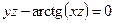
4. а) 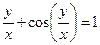 б)
б) 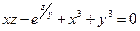
5. а) 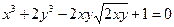 б)
б) 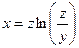
6. а) 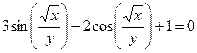 б)
б) 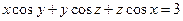
7. а) 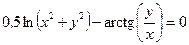 б)
б) 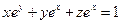
8. а) 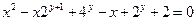 б)
б) 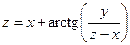
9. а) 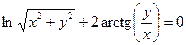 б)
б) 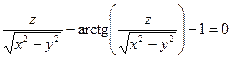
10. а) 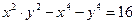 б)
б) 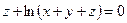
11. а) 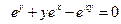 б)
б) 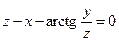
12. а) 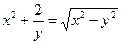 б)
б) 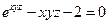
13. а) 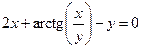 б)
б) 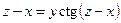
14. а) 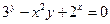 б)
б) 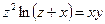
15. а) 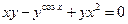 б)
б) 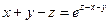
16. а) 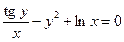 б)
б) 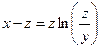
17. а) 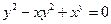 б)
б) 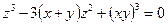
18. а) 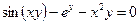 б)
б) 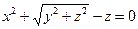
19. а) 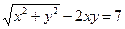 б)
б) 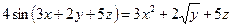
20. а) 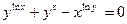 б)
б) 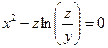
21. а) 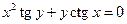 б)
б) 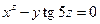
22. а) 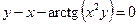 б)
б) 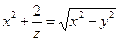
23. а) 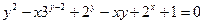 б)
б) 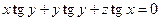
24. а) 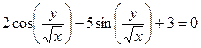 б)
б) 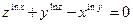
25. а) 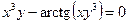 б)
б) 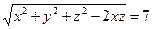
26. а) 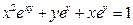 б)
б) 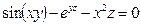
27. а) 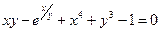 б)
б) 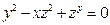
28. а) 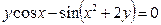 б)
б) 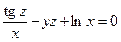
29. а) 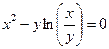 б)
б) 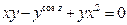
30. а) 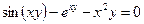 б)
б) 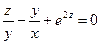
Задание №7.
Найти производную указанной функции в направлении вектора 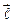 в точке М и градиент этой функции в точке М.
в точке М и градиент этой функции в точке М.
1. а) 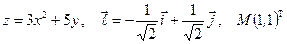
б) 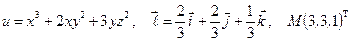
2. а) 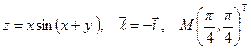
б) 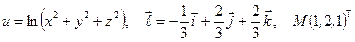
3. а) 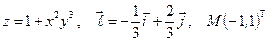
б) 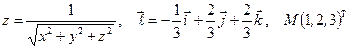
4. а) 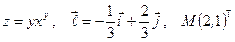
б) 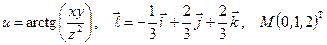
5. а) 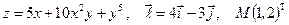
б) 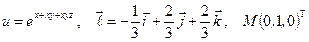
6. а) 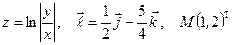
б) 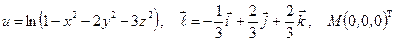
7. а) 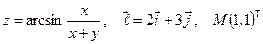
б) 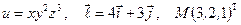
8. а) 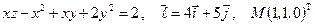
б) 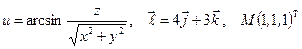
9. а) 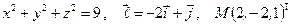
б) 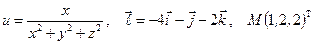
10. а) 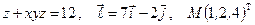
б) 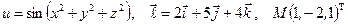
11. а) 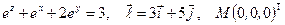
б) 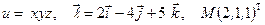
12. а) 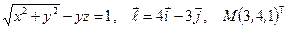
б) 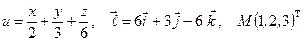
13. а) 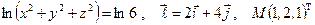
б) 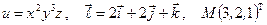
14. а) 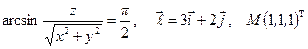
б) 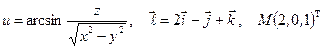
15. а) 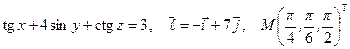
б) 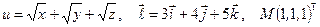
16. а) 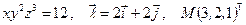
б) 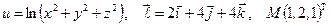
17. а) 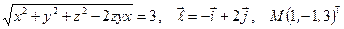
б) 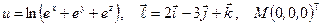
18. а) 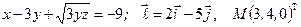
б) 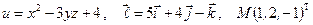
19. а) 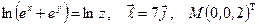
б) 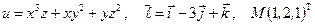
20. а) 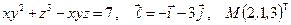
б) 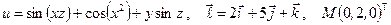
21. а) 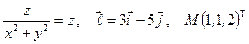
б) 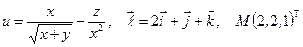
22. а) 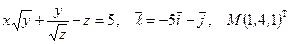
б) 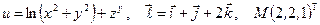
23. а) 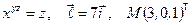
б) 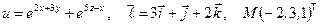
24. а) 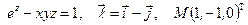
б) 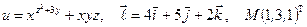
25. а) 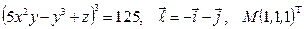
б) 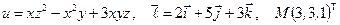
26. а) 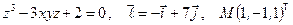
б) 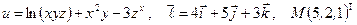
27. а) 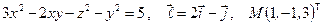
б) 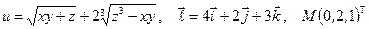
28. а) 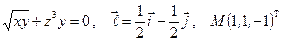
б) 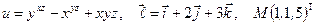
29. а) 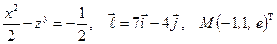
б) 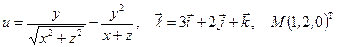
30. а) 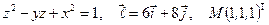
б) 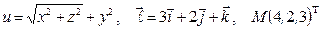
Задание№8.
Написать уравнения касательной плоскости и нормали к поверхности S в точке М. Линеаризовать функцию 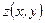 в точке М.
в точке М.
1. 
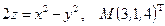
2. 
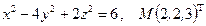
3. 
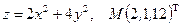
4. 
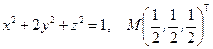
5. 
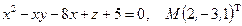
6. 
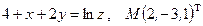
7. 
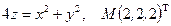
8. 
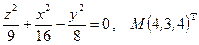
9. 
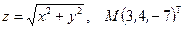
10. 
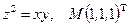
11. 
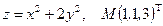
12. 
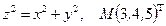
13. 
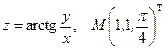
14. 
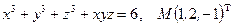
15. 
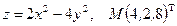
16. 
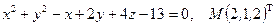
17. 
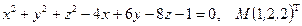
18. 
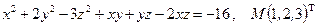
19. 
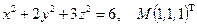
20. 
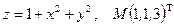
21. 
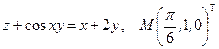
22. 
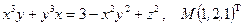
23. 
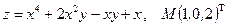
24. 
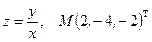
25. 
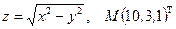
26. 
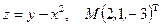
27. 
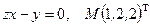
28. 
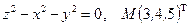
29. 
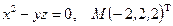
30. 
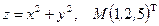
Задание№9.
Исследовать на экстремум функцию 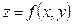 .
.
Задание№10.
Найти наибольшее и наименьшее значение функции 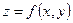 в треугольнике АВС, который задан координатами своих вершин.
в треугольнике АВС, который задан координатами своих вершин.
ПРИМЕР ВЫПОЛНЕНИЯ ЗАДАНИЙ САМОСТОЯТЕЛЬНОЙ РАБОТЫ СТУДЕНТОВ
Пример выполнения задания 1 а)
Условие.Найти и изобразить область определения функции 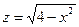
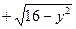 .
.
Решение.
1) Заданная функция двух переменных определена, если подкоренное выражение в каждом слагаемом неотрицательно, т.е. выполняется система двух неравенств: 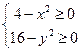 .
.
2) Решая эту систему, получим 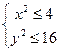 , откуда
, откуда 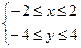 .
.
3) Таким образом, область определения 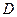 данной функции – внутренность прямоугольника, ограниченного прямыми
данной функции – внутренность прямоугольника, ограниченного прямыми 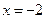 ,
, 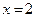 и
и 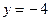 ,
, 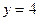 , которая изображена на рисунке 1.
, которая изображена на рисунке 1.
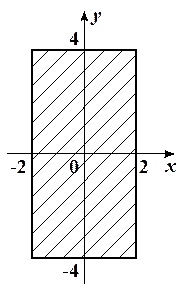
Рис. 1
Пример выполнения задания 1 б)
Условие. Найти и изобразить область определения функции 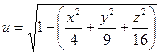 .
.
Решение.
1) Заданная функция трёх переменных определена, если подкоренное выражение неотрицательно, т.е. выполняется неравенство: 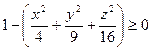 . Откуда получим
. Откуда получим 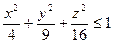 .
.
2) Это неравенство задаёт внутренность эллипсоида с полуосями соответственно: 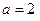 по оси ОХ,
по оси ОХ,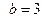 по оси ОY,
по оси ОY, 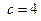 по оси ОZ.
по оси ОZ.
3) Таким образом, область определения 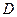 данной функции является внутренность эллипсоида, которая изображена на рисунке 2.
данной функции является внутренность эллипсоида, которая изображена на рисунке 2.
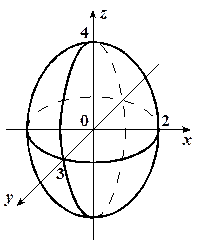
Рис. 2
Пример выполнения задания 2 а)
Условие. Найти дифференциалы первого и второго порядка (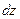 и
и 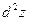 ) функции
) функции 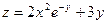 .
.
Решение.
1) Найдем частные производные первого порядка заданной функции двух переменных.
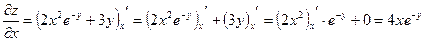 ;
;
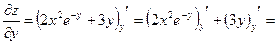
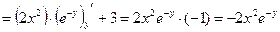 .
.
2) Найдем полный дифференциал первого порядка указанной функции.
В соответствии с формулой
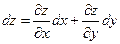 (2.4)
(2.4)
он принимает вид: 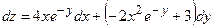 .
.
3) Найдем частные производные второго порядка заданной функции.
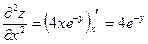 ;
;
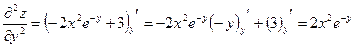 ;
;
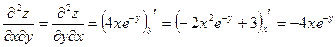 .
.
4) Найдем полный дифференциал второго порядка.
В соответствии с формулой
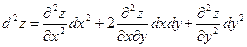 (6.1)
(6.1)
он принимает вид 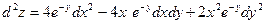 .
.
ОТВЕТ.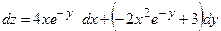 ,
,
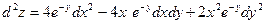 .
.
Пример выполнения задания 2 б)
Условие.Найти дифференциалы первого и второго порядка (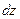 и
и 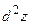 ) функции
) функции 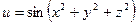 .
.
Решение.
1) Найдем частные производные первого порядка заданной функции трех
переменных.
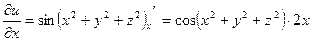 ;
;
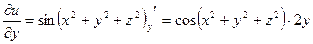 ;
;
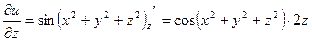 .
.
2) Найдем сначала полный дифференциал первого порядка.
В соответствии с формулой
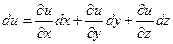 (2.5)
(2.5)
он принимает вид: 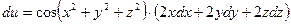 .
.
3) Найдем частные производные второго порядка.
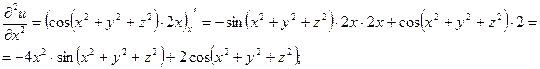
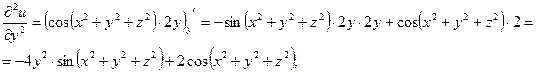
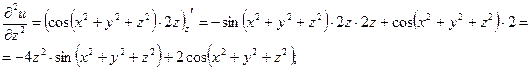
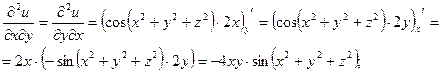
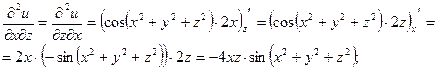
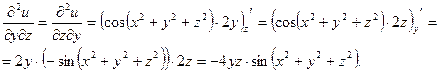
4) Найдем полный дифференциал второго порядка заданной функции.
В соответствии с формулой  (6.5)
(6.5)
он принимает вид:
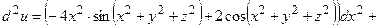
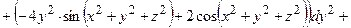
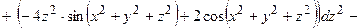
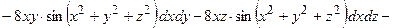
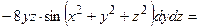
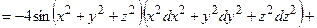
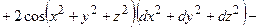
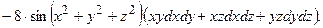
ОТВЕТ.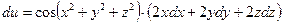 ,
,
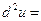
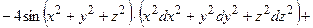
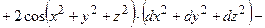
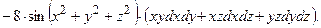
Пример выполнения задания 3
Условие.Вычислить приближенно 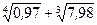 , считая
, считая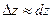 .
.
Решение.
1) Рассмотрим функцию 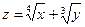 .
.
2) Тогда искомое выражение 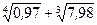 можно представить в виде:
можно представить в виде: 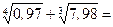
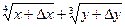 ,
,
где 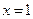 ,
, 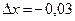 ,
, 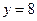 ,
, 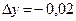 .
.
3) Найдем частные производные функции 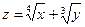 .
.
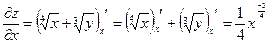 ,
,
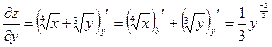 .
.
4) Используя формулу для приближенных вычислений с помощью полного дифференциала
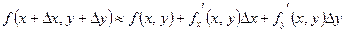 (2.6),
(2.6),
получим приближенное значение выражения: 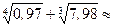
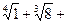
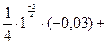
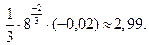
ОТВЕТ.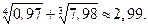
Пример выполнения задания 4 а)
Условие. Найти производную 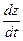 сложной функции
сложной функции 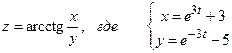 .
.
Решение.
1) Найдем частные производные, входящие в формулу
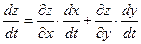 . (3.1)
. (3.1)
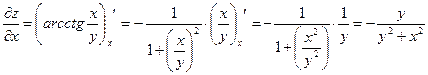 ;
;
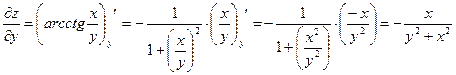 ;
;
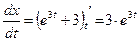 ;
; 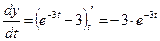 .
.
2) Используя формулу (3.1), получим:
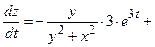
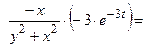
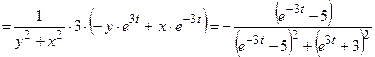 .
.
ОТВЕТ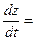
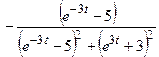 .
.
Пример выполнения задания 4 б)
Условие. Найти частные производные 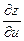 и
и 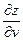 функции
функции 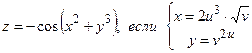 .
.
Решение.
1) Найдем все частные производные, входящие в формулы (3.3)
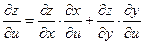 и
и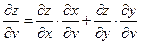
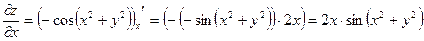 ;
;
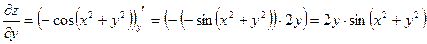 ;
;
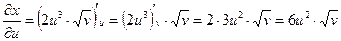 ;
;
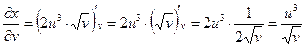 ;
;
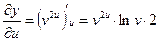 ;
; 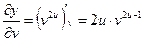 .
.
2) В соответствии с формулами (3.3) получим:
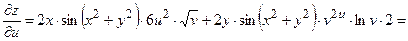
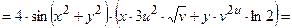
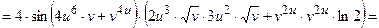
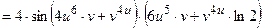 ;
;
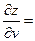
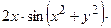
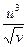 +
+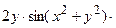
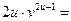
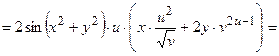
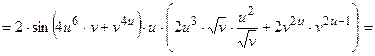
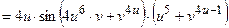 .
.
ОТВЕТ.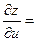
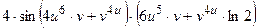 ,
,
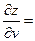
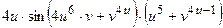 .
.
Пример выполнения задания 5 а)
Условие. Показать, что функция 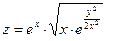 удовлетворяет уравнению
удовлетворяет уравнению 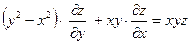 .
.
Решение.
1) Упростим заданную функцию
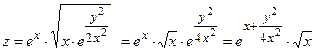 .
.
2) Найдем все частные производные, входящие в уравнение.
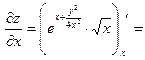
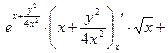
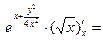
=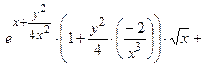
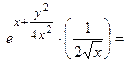
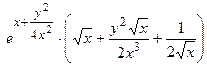 ;
;
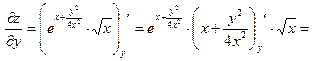

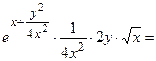
=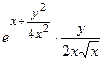 .
.
3) Подставим найденные производные в исходное уравнение:
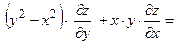
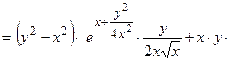
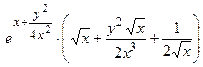 =
=
=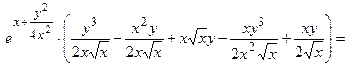
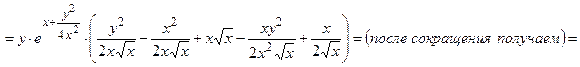
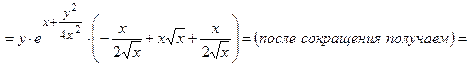
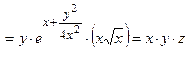 , что и требовалось показать.
, что и требовалось показать.
Пример выполнения задания 5 б)
Условие. Показать, что функция 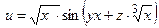 удовлетворяет
удовлетворяет
уравнению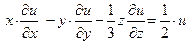 .
.
Решение.
1) Найдем все частные производные, входящие в уравнение.
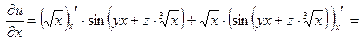
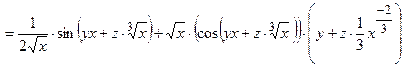 ;
;
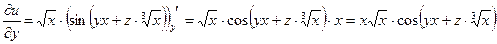 ;
;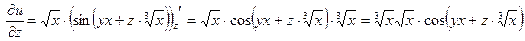 .
.
2. Подставим найденные производные в исходное уравнение
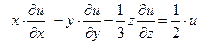 .
.
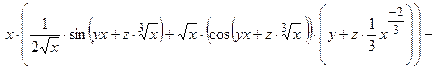
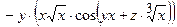
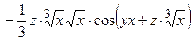 =
=
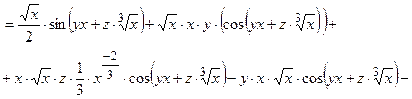
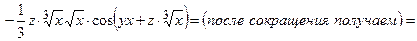
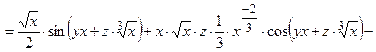
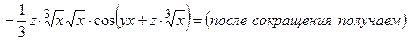 =
=
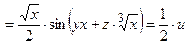 , что и требовалось показать.
, что и требовалось показать.
Пример выполнения задания 6 а)
Условие.Найти производную 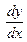 неявной функции
неявной функции 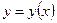 , заданной уравнением
, заданной уравнением 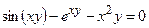 .
.
Решение.
1) Здесь 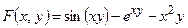 =0.
=0.
2) Производную неявной функции 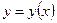 , заданной с помощью уравнения
, заданной с помощью уравнения 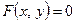 , можно найти по формуле
, можно найти по формуле
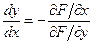 , при условии
, при условии 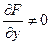 (3.4),
(3.4),
где 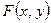 – дифференцируемая функция переменных
– дифференцируемая функция переменных 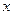 и
и 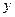 .
.
Найдем частные производные
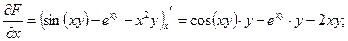
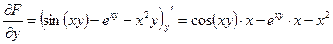 .
.
3) По формуле (3.4) получаем 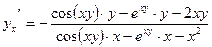 .
.
ОТВЕТ.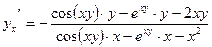 .
.
Пример выполнения задания 6 б)
Условие.Найти частные производные 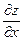 и
и 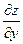 неявной функции
неявной функции 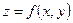 , заданной уравнением
, заданной уравнением 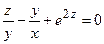 .
.
Решение.
1) Здесь 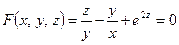 .
.
2) Частные производные неявной функции двух переменных 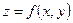 , заданной уравнением
, заданной уравнением 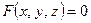 , вычисляются по формулам:
, вычисляются по формулам:
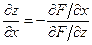 ,
, 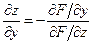 , при условии, что
, при условии, что 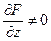 (3.5)
(3.5)
3) Найдем частные производные функции 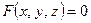
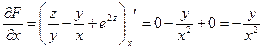 ;
;
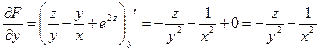 ;
;
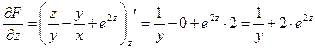 .
.
4) Частные производные неявной функции двух переменных 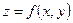 , определяются следующим образом:
, определяются следующим образом:
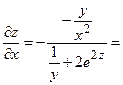
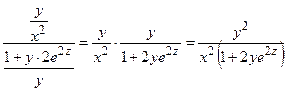 ;
;
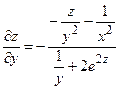 =
=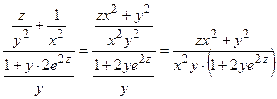 .
.
ОТВЕТ.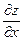
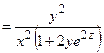 ,
, 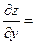
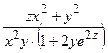 .
.
Пример выполнения задания 7 а)
Условие.Найти производную функции  в точке
в точке 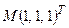 в направлении вектора
в направлении вектора 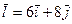 и градиент функции в этой точке.
и градиент функции в этой точке.
Решение.
1) Производная в направлении вектора 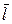 определяется по формуле
определяется по формуле
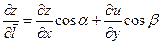 (5.2)
(5.2)
где 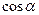 ,
, 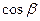 – направляющие косинусы вектора
– направляющие косинусы вектора 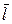 .
.
2) Найдем частные производные заданной функции и вычислим их значения в точке 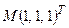 :
:
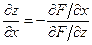 ,
, 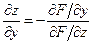 , при условии
, при условии 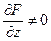 .
.
Получим 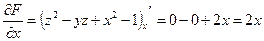 ;
;
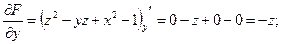
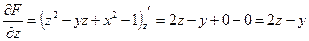 .
.
3) Тогда частные производные неявной функции двух переменных 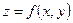 , определяются следующим образом:
, определяются следующим образом:
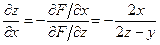 ;
; 
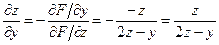 .
.
4) Вычислим значения частных производных в точке 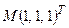 :
:
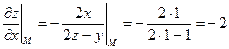 ;
; 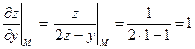 .
.
5) Найдем длину вектора 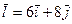 и его направляющие косинусы:
и его направляющие косинусы:
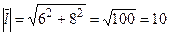 ;
;
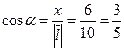 ;
; 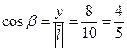 .
.
6) Используя формулу (5.2), получим производную функции z в направлении вектора 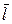 :
:
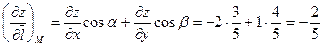 .
.
7) По формуле 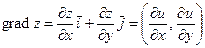 (5.3) имеем:
(5.3) имеем: 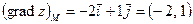 .
.
ОТВЕТ.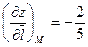 ,
, 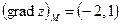 .
.
Пример выполнения задания 7 б)
Условие.Найти производную функции 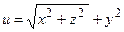 в точке
в точке 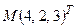 в направлении вектора
в направлении вектора 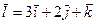 и градиент функции в этой точке.
и градиент функции в этой точке.
Решение.
1) Производная в направлении вектора 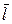 определяется по формуле
определяется по формуле
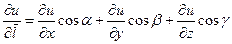 , (5.2)
, (5.2)
где 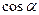 ,
, 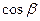 ,
, 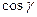 – направляющие косинусы вектора
– направляющие косинусы вектора 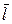 .
.
2) Найдем частные производные заданной функции и вычислим их значения в точке 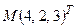 .
.
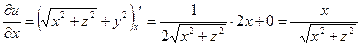 ,
,
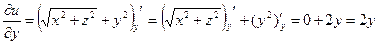 ,
,
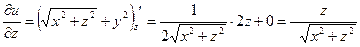 ;
;
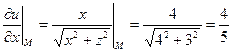 ;
;
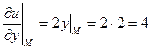 ;
;
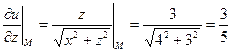 .
.
3) Найдем длину вектора 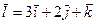 и его направляющие косинусы:
и его направляющие косинусы:
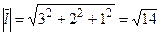 ;
;
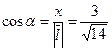 ;
; 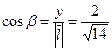 ;
; 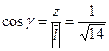 .
.
4) Используя формулу (5.2), получим производную функции u в направлении вектора 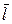 :
:
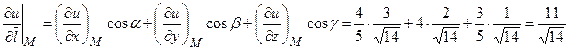 .
.
5) По формуле
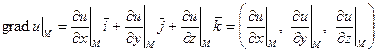 (5.3)
(5.3)
получим 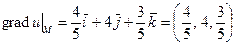 .
.
ОТВЕТ. 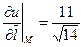 ,
, 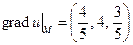 .
.
Пример выполнения задания 8
Условие. Написать уравнения касательной плоскости и нормали к поверхности 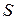 , заданной функцией
, заданной функцией 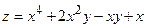 в точке
в точке 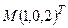 . Линеаризовать данную функцию в точке
. Линеаризовать данную функцию в точке 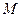 .
.
Решение.
1) Выясним, принадлежит ли точка 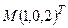 заданной поверхности.
заданной поверхности.
Для этого подставим координаты точки М в уравнение поверхности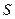 :
:
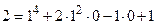 =2; то есть 2=2,
=2; то есть 2=2,
следовательно, точка 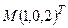 принадлежит заданной поверхности
принадлежит заданной поверхности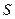 .
.
2) Так как поверхность 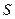 задана явно функцией
задана явно функцией 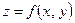 , то уравнение касательной плоскости имеет вид
, то уравнение касательной плоскости имеет вид
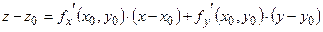 , (4.1)
, (4.1)
а уравнение нормали –
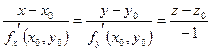 . (4.2)
. (4.2)
3) Найдем значения частных производных функции 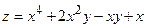 в точке
в точке 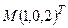 .
.
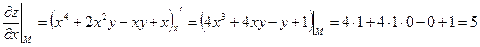
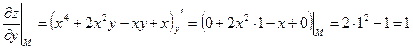 .
.
4) Используя формулы (4.1) и (4.2), получим соответственно уравнение касательной плоскости 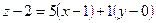 или
или 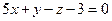 , и уравнение нормали
, и уравнение нормали 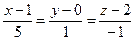 .
.
5) Линеаризовать функцию двух переменных в точке М – значит провести касательную плоскость к поверхности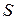 в этой точке. Выразим из уравнения касательной плоскости z, получим
в этой точке. Выразим из уравнения касательной плоскости z, получим 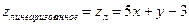 .
.
2–й способ линеаризации:
Линеаризацией функции 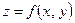 в точке
в точке 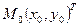 называется функция вида
называется функция вида
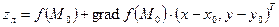 . (5.5)
. (5.5)
Так как 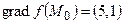 , то линеаризация функции
, то линеаризация функции 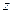 принимает вид:
принимает вид: 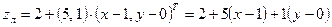 или
или 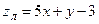 .
.
ОТВЕТ.Уравнение касательной плоскости 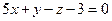 ,
,
уравнение нормали 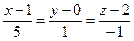 ,
, 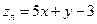 .
.
Пример выполнения задания 9
Условие. Исследовать на экстремум функцию 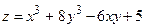 .
.
Решение.
1) Проверим необходимые условия существования экстремума. Для этого найдем частные производные первого порядка и приравняем их к нулю:
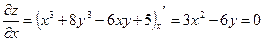 ,
,
 .
.
2) Получим систему двух нелинейных уравнений 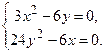
Решение системы – координаты стационарных точек.
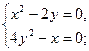
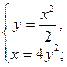
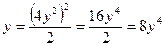 ;
;
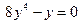 ;
; 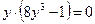 ;
; 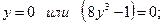
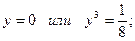
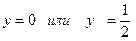 .
.
Так как 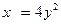 , то
, то 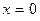 или
или 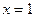 .
.
Получим две стационарные точки 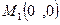 и
и 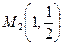 .
.
3) Проверим достаточные условия существования экстремума. Для этого:
а) найдем частные производные второго порядка и вычислим их значения в стационарных точках 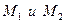 .
.
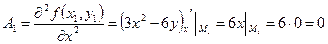 ;
;
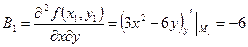 ;
;
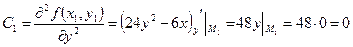 ;
;
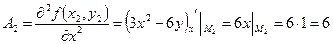 ;
;
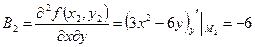 ;
;
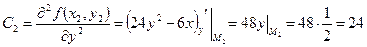 .
.
б) составим выражение 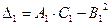 и определим его знак:
и определим его знак:
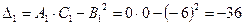
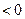 .
.
Так как 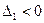 , то в точке
, то в точке 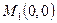 экстремума нет.
экстремума нет.
в) составим выражение 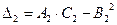 и определим его знак:
и определим его знак:
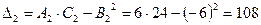
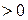 .
.
Так как 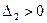 , то в точке
, то в точке 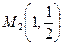 существует экстремум, а именно, минимум, поскольку
существует экстремум, а именно, минимум, поскольку 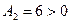 .
.
4) Вычислим значение исходной функции в точке минимума:
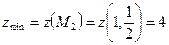 .
.
ОТВЕТ.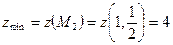 .
.
Пример выполнения задания 10
Условие. Найти наибольшее и наименьшее значения функции 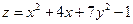 в треугольнике
в треугольнике 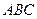 , который задан координатами своих вершин
, который задан координатами своих вершин 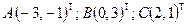 .
.
Решение.
1) Замкнутая область D – треугольник 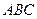 , изображенный на рисунке 3.
, изображенный на рисунке 3.
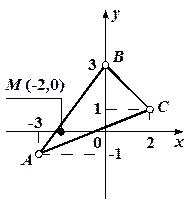
Рис. 3
2) Найдем стационарные точки заданной функции, принадлежащие 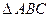 , и вычислим значения функции в этих точках.
, и вычислим значения функции в этих точках.
а) Для этого найдем частные производные первого порядка и приравняем их к нулю:
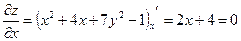 ;
;
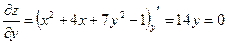 .
.
Решением полученной системы уравнений 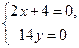 является
является 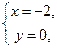
т.е. точка 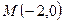 – стационарная, принадлежит треугольнику
– стационарная, принадлежит треугольнику 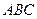 .
.
б) Вычислим значение функции в точке 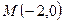 :
:
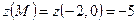 .
.
3) Найдем наибольшее и наименьшее значения функции на линиях, образующих границу 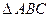 .
.
а) Составим уравнения прямых, образующих 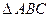 . Для этого используем формулу уравнения прямой
. Для этого используем формулу уравнения прямой 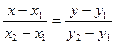 , проходящей через две заданные точки
, проходящей через две заданные точки 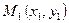 и
и 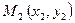 .
.
б) Прямая 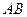 , проходящая через точки
, проходящая через точки 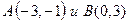 , задается уравнением
, задается уравнением 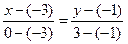 или
или 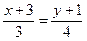 , откуда
, откуда 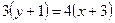 или
или 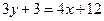 или
или 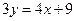 .
.
Итак, уравнение прямой 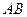 имеет вид:
имеет вид: 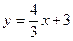 , где
, где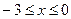 .
.
Подставим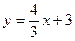 в исходную функцию
в исходную функцию 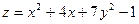 .
.
Получим 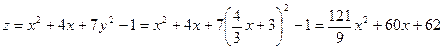 .
.
Исследуем полученную функцию 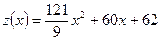 на экстремум. Для этого найдем критические точки этой функции:
на экстремум. Для этого найдем критические точки этой функции:
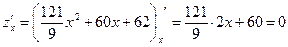 , откуда
, откуда 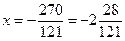 критическая точка, принадлежащая отрезку
критическая точка, принадлежащая отрезку 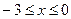 .
.
Найдем значения функции в этой точке и на концах отрезка 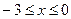 .
.
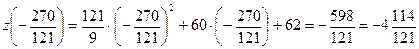 ;
; 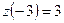 ;
; 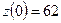 .
.
в) Прямая 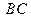 , проходящая через точки
, проходящая через точки 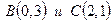 , задается уравнением
, задается уравнением
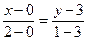 или
или 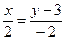 , откуда
, откуда 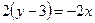 или
или 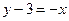 .
.
Итак, уравнение прямой 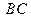 имеет вид:
имеет вид: 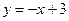 , где
, где 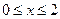 .
.
Подставим 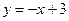 в исходную функцию
в исходную функцию 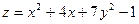 .
.
Тогда 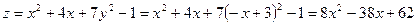 .
.
Исследуем полученную функцию 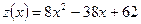 на экстремум. Для этого найдем критические точки этой функции:
на экстремум. Для этого найдем критические точки этой функции:
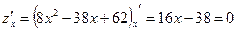 , откуда
, откуда 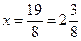 критическая точка, не принадлежащая отрезку
критическая точка, не принадлежащая отрезку 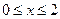 .
.
Найдем значения функции на концах отрезка 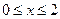
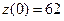 ;
; 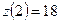 .
.
г) Прямая 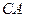 , проходящая через точки
, проходящая через точки 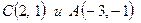 , задается уравнением
, задается уравнением 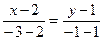 или
или 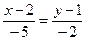 , откуда
, откуда 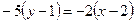 или
или 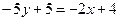 ;
; 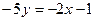 .
.
Итак, уравнение прямой 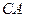 имеет вид:
имеет вид: 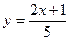 , где
, где 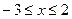 .
.
Подставим 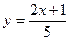 в исходную функцию
в исходную функцию 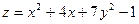 .
.
Тогда 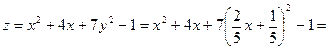
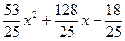 ..
..
Исследуем функцию 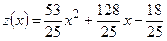 на экстремум.
на экстремум.
Для этого найдем критические точки этой функции:
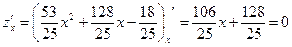 , откуда
, откуда 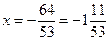 критическая точка, принадлежащая отрезку
критическая точка, принадлежащая отрезку 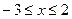 .
.
Найдем значения функции в этой точке и на концах отрезка 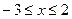 .
.
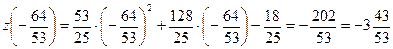 ;
;
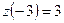 ;
; 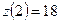 .
.
4) Из всех найденных значений функции выберем наибольшее и наименьшее.
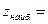
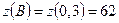 ,
, 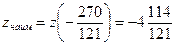 .
.
ОТВЕТ.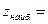
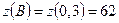 ,
, 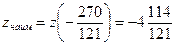 .
.
Приложение
Для самоконтроля правильности нахождения частных производных можно воспользоваться системой MathCad. Чтобы вычислить частную производную, необходимо ввести оператор производной с панели Calculus (Вычисления) и в соответствующем местозаменителе (контекстном меню) напечатать имя переменной, по которой должно быть осуществлено дифференцирование.
Пример 1. Аналитическое вычисление частных производных.
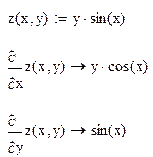
Пример 2. Символьное и численное вычисления частных производных в точке.
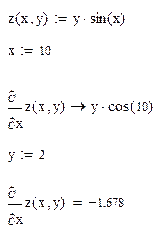
Пример 3. Вычисление частных производных второго порядка.
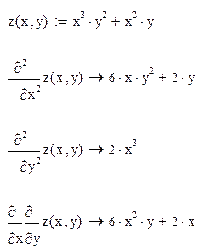
Литература
1. Пискунов Н.С. Дифференциальное и интегральное исчисление. т.1,2. –– М.: Наука, 1978г.
2. Бугров Я.С., Никольский С.М. Дифференциальное и интегральное исчисление. –– М.: Наука, 1980г.
3. Данко П.Е. и др. Высшая математика в упражнениях и задачах. ч. 1 –– М.: Высшая школа, 1980г.
4. Вся высшая математика: Учебник для втузов (МО). Т. 2.: Интегральное исчисление. Дифференциальное исчисление функций нескольких переменных. Дифференциальная геометрия /Краснов М.Л., Киселев А.И. и др. 2-изд., испр. М.: Едиториал УРСС, 2004.
5. Л. Д. Кудрявцев, А.Д. Кутасов, В. И. Чехлов, М. И. Шабунин. Сборник задач по математическому анализу. Функции нескольких переменных: Учеб. пособие для вузов/Под ред. Л.Д. Кудрявцева. Санкт-Петербург, 1994, 496 с.
6. Плис А.И., Сливина Н.А. Mathcad 2000. Математический практикум для экономистов и инженеров. Учебное пособие. М.: Финансы и статистика, 2000, 656 с.
– Конец работы –
Используемые теги: Дегтярева0.041
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: В.А. Дегтярева
Что будем делать с полученным материалом:
Если этот материал оказался полезным для Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?


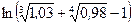
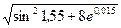
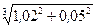
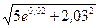
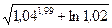
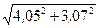
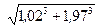
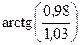
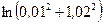
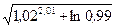
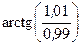
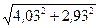
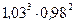
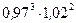
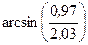
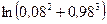
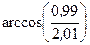
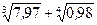
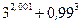
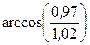
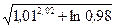
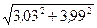
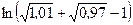
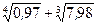
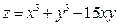
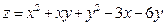
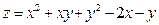
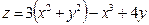
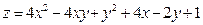
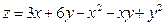
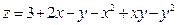
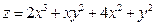
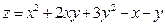
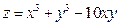
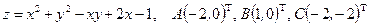
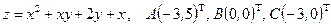
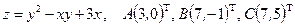
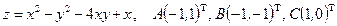
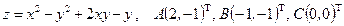
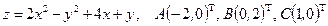
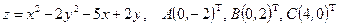
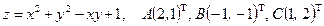
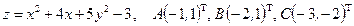
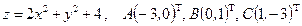
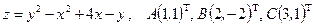
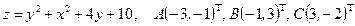
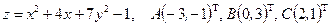





Новости и инфо для студентов