Производная сложной и неявной функции
Пусть 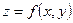 – функция двух переменных
– функция двух переменных 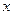 и
и 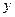 , каждая из которых является функцией независимой переменной
, каждая из которых является функцией независимой переменной 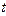 , т.е.
, т.е. 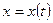 ,
, 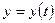 .
.
Если 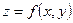 – дифференцируемая в точке
– дифференцируемая в точке 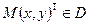 функция, а аргументы
функция, а аргументы 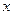 и
и 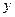 – дифференцируемые функции независимой переменной
– дифференцируемые функции независимой переменной 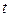 , т.е.
, т.е. 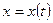 и
и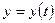 , то производная сложной функции
, то производная сложной функции 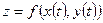 одной переменной
одной переменной 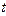 вычисляется по формуле
вычисляется по формуле
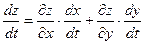 (3.1).
(3.1).
Если переменная 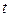 совпадает с одним из аргументов
совпадает с одним из аргументов 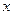 или
или 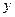 , например
, например 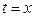 , то производная сложной функции
, то производная сложной функции 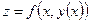 одной переменной
одной переменной 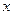 находится по формуле
находится по формуле
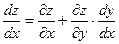 (3.2)
(3.2)
и называется полной производной.
Если 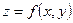 – функция двух переменных
– функция двух переменных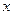 и
и 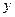 , а аргументы
, а аргументы 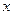 ,
,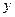 являются функциями двух переменных
являются функциями двух переменных 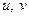 , т.е.
, т.е. 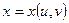 и
и 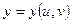 , то функция
, то функция 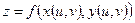 является функцией двух переменных
является функцией двух переменных 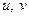 . Тогда её частные производные
. Тогда её частные производные 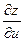 и
и 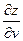 выражаются так:
выражаются так:
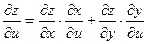 и
и 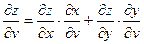 . (3.3)
. (3.3)
Пример 3.1. Найти полную производную 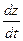 , если
, если 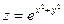 и
и 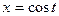 ,
, 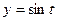 .
.
Решение. Найдем частные производные
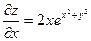 ,
, 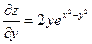 ,
, 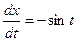 ,
, 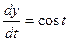 .
.
Согласно формуле (3.1) получим:
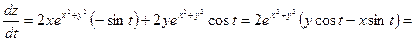
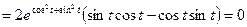 .
.
Пример 3.2. Найти частные производные 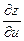 и
и 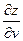 сложной функции
сложной функции 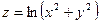 , если
, если 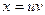 ,
, 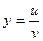 .
.
Решение. Найдем частные производные
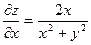 ,
, 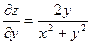 ,
,
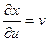 ,
, 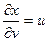 ,
, 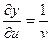 ,
, 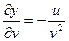 .
.
По формулам (3.3) получим:
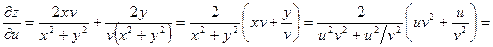
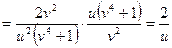 ;
;
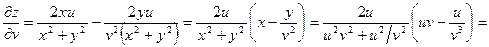
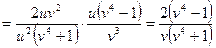 .
.
Пусть функция 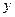 от
от 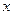 задается неявно с помощью уравнения
задается неявно с помощью уравнения 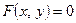 .Тогда производная неявной функции
.Тогда производная неявной функции 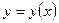 , где
, где 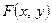 – дифференцируемая функция переменных
– дифференцируемая функция переменных 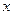 и
и 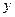 , вычисляется по формуле
, вычисляется по формуле
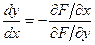 , при условии
, при условии 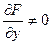 . (3.4)
. (3.4)
Аналогично, если неявная функция двух переменных 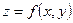 задаётся с помощью уравнения
задаётся с помощью уравнения 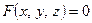 , где
, где 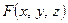 – дифференцируемая функция переменных
– дифференцируемая функция переменных 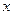 ,
, 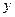 и
и 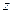 , то её частные производные определяются по формулам
, то её частные производные определяются по формулам
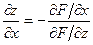 ,
, 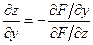 , при условии
, при условии 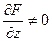 . (3.5)
. (3.5)
Пример 3.3. Найти производную 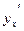 , если неявная функция задана уравнением
, если неявная функция задана уравнением 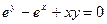 .
.
Решение. Здесь 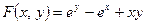 .
.
Найдем 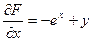 ,
, 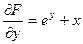 .
.
Тогда получим 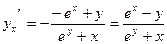 .
.
Пример 3.4. Найти частные производные 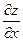 и
и 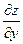 , если неявная функция задана уравнением
, если неявная функция задана уравнением 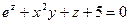 .
.
Решение. Здесь 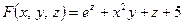 .
.
Найдем 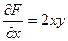 ,
, 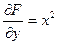 ,
, 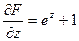 .
.
Тогда 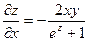 и
и 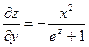 .
.