Производная по направлению. Градиент. Линеаризация
Производной функции 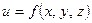 в точке
в точке 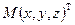 по направлению вектора
по направлению вектора 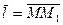 называется предел
называется предел
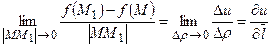 , где
, где 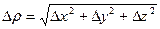 . (5.1)
. (5.1)
Если функция 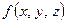 дифференцируема, то производная по направлению вектора
дифференцируема, то производная по направлению вектора 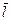 находится по формуле
находится по формуле
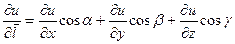 , (5.2)
, (5.2)
где 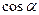 ,
, 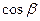 ,
, 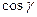 – направляющие косинусы вектора
– направляющие косинусы вектора 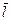 .
.
Градиентом функции 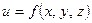 в точке
в точке 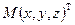 называется вектор с началом в точке
называется вектор с началом в точке 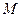 , координатами которого являются значения частных производных функции
, координатами которого являются значения частных производных функции 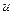 в этой точке:
в этой точке:
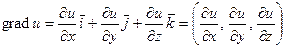 . (5.3)
. (5.3)
Градиент функции 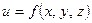 и производная по направлению вектора
и производная по направлению вектора 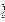 связаны формулой
связаны формулой 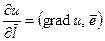 (5.4),
(5.4),
где 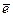 – орт вектора
– орт вектора 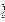 , который находится по формуле
, который находится по формуле 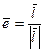 .
.
Линеаризацией функции 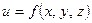 в точке
в точке 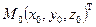 называется функция вида
называется функция вида
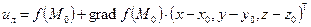 . (5.5)
. (5.5)
Пример 5.1. Найти градиент и производную функции 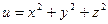 по направлению вектора
по направлению вектора 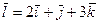 в точке
в точке 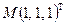 . Линеаризовать данную функцию в точке
. Линеаризовать данную функцию в точке 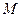 .
.
Решение. Найдем частные производные заданной функции в точке 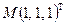 :
:
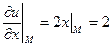 ,
, 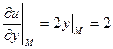 ,
, 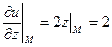 .
.
По формуле (5.3) получим: 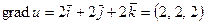 .
.
Найдем орт вектора 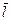
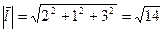 ,
, 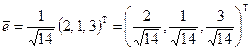
и его направляющие косинусы:
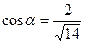 ,
, 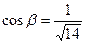 ,
, 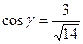 .
.
Согласно формуле (5.4) или (5.2) определим производную по направлению:
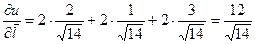 .
.
Найдем значение функции в точке 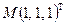 :
: 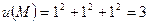 .
.
Тогда линеаризация функции 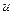 по формуле (5.5) принимает вид:
по формуле (5.5) принимает вид:
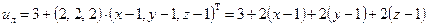 ,
,
или
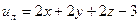 .
.