Частные производные и дифференциалы высших порядков
Частными производными второго порядка от функции 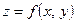 называются частные производные от ее частных производных первого порядка.
называются частные производные от ее частных производных первого порядка.
Обозначения частных производных второго порядка
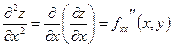 ;
; 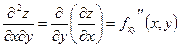 ;
;
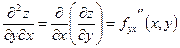 ;
; 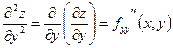 .
.
Аналогично определяются и обозначаются частные производные третьего и высших порядков, например:
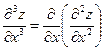 ;
; 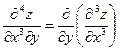 и т.д.
и т.д.
Частные производные второго и более высокого порядка, взятые по разным переменным, называются смешанными частными производными, например: 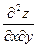 ,
, 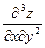 ,
, 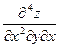 и т.д.
и т.д.
Теорема (Шварца). Если функция 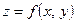 и её частные производные первого и второго порядка определены и непрерывны в некоторой окрестности точки
и её частные производные первого и второго порядка определены и непрерывны в некоторой окрестности точки 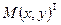 , то смешанные производные одного порядка, отличающиеся только порядком дифференцирования, равны между собой
, то смешанные производные одного порядка, отличающиеся только порядком дифференцирования, равны между собой 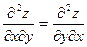 .
.
Пример 6.1. Найти частные производные второго порядка функции 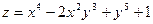 .
.
Решение. Последовательно найдем частные производные первого и второго порядка
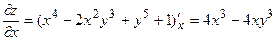 ;
; 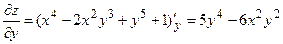 ;
;
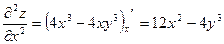 ;
;
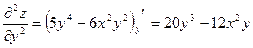 ;
;
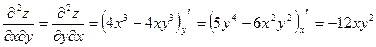 .
.
Дифференциалом второго порядка от функции 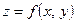 называется дифференциал от ее полного дифференциала первого порядка, т.е.
называется дифференциал от ее полного дифференциала первого порядка, т.е. 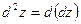 .
.
Аналогично определяются дифференциалы третьего и высших порядков 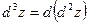 ; …,
; …, 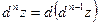 .
.
Если функция двух переменных 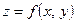 имеет непрерывные частные производные по независимым переменным
имеет непрерывные частные производные по независимым переменным 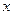 и
и 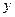 , то дифференциалы высших порядков определяются по формулам
, то дифференциалы высших порядков определяются по формулам
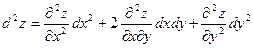 ; (6.1)
; (6.1)
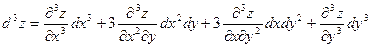 . (6.2)
. (6.2)
В общем случае имеет место символическая формула
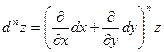 . (6.3)
. (6.3)
Для функции трех переменных 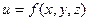 символическая формула дифференциала
символическая формула дифференциала 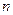 - го порядка имеет вид:
- го порядка имеет вид:
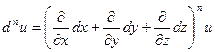 . (6.4)
. (6.4)
Формула дифференциала второго порядка для функции трех переменных имеет вид:
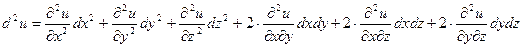 . (6.5)
. (6.5)
Пример 6.2. Найти дифференциал второго порядка 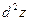 , если функция
, если функция 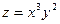 .
.
Решение. Найдем все частные производные первого и второго порядка заданной функции
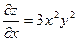 ,
, 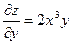 ,
,
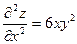 ,
, 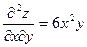 ,
, 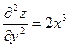 .
.
Согласно формуле (6.1) получим
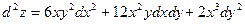 .
.