Линейная аппроксимация
Аппроксимирующую линейную функцию еще называют линией регрессии. Задача линейной аппроксимации сводится к определению параметров линейной функции y=ax+b, то есть ее коэффициентов a и b. Последовательность решения этой задачи следующая:
– исходя из метода наименьших квадратов, записывается выражение для определения суммы квадратов отклонений в виде функции S:
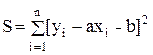 (22.4)
(22.4)
– дифференцируется выражение (22.4) по a и b, и формируется система линейных уравнений, решение которых дает следующие значения параметров:
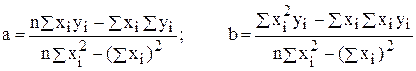 (22.5)
(22.5)
Подобранная прямая называется линией регрессии y на x, коэффициенты a и b называются коэффициентами регрессии.
Чем меньше величина
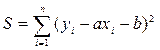 ,
,
тем более обосновано предположение, что табличная зависимость описывается линейной функцией. Существует показатель, характеризующий тесноту линейной связи между xи y. Он называется коэффициентом корреляции.
Коэффициент корреляции рассчитывается по формуле:
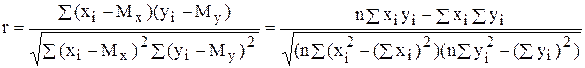
Коэффициент корреляции r и коэффициент регрессии a связаны соотношением
 ,
,
где Dy, Dx – среднеквадратичное отклонение значений x и y.

Значение коэффициента корреляции удовлетворяет условию –1 £ r £ 1. Чем меньше отличается абсолютная величина r от единицы, тем ближе к линии регрессии располагаются экспериментальные точки. Если коэффициент корреляции равен нулю (r=0), то переменные x и y называются некоррелированными, и это означает, что между x и y не существует линейной связи, но между ними может существовать другая зависимость, отличная от линейной. Из этого следует, что аппроксимация с помощью линейной функции неудачна, и необходимо искать другой вид аппроксимирующей функции (нелинейной).
На практике для оценки степени взаимосвязи между параметрами можно руководствоваться следующими эмпирическими правилами:
– при 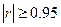 – практически линейная корреляция,
– практически линейная корреляция,
– при 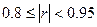 – сильная степень линейной связи между параметрами,
– сильная степень линейной связи между параметрами,
– при  – линейная связь между параметрами существует,
– линейная связь между параметрами существует,
– при 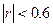 – линейная связь между параметрами отсутствует.
– линейная связь между параметрами отсутствует.