Вільні коливання точки при відсутності опору

 

Розглянемо загальний випадок прямолінійних коливань матеріальної точки на прикладі конструкції, показаної на рис. 2.1.

Тверде тіло М масою т (механічний агрегат) з’єднується з горизонтальною площиною через пружину. Направляючі забезпечують рух тіла М тільки у вертикальному напрямку.

При переміщенні тіла М пружина буде деформуватись (стискатись чи розтягуватись), в результаті чого виникне поновлююча сила 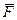(сила пружності), яка прагнутиме повернути тіло М в положення рівноваги. Модуль цієї сили пропорційний деформації пружини, або віддалі х від положення рівноваги

,

де с – коефіцієнт жорсткості пружини.

На тіло М діє також постійна сила 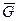(сила ваги), направлена вертикально вниз. Під дією цієї сили пружина стиснеться на величину _ст, яка називається статичним відхиленням.

Розглянемо рух тіла М під дією вказаних сил.

В положенні статичної рівноваги сила пружності врівноважується силою ваги

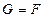, або .

Виведемо тіло М з положення рівноваги, стиснувши пружину. Дію сил у цьому випадку можна зобразити схемою, показаною на рис. 10.5.

В цій схемі тіло М, прийняте за матеріальну точку, показане в довільному положенні на осі х, яка направлена вниз. Початок відліку О по осі х відповідає положенню статичної рівноваги точки М при дії постійної сили .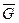

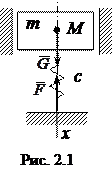Рух точки М описується диференціальним рівнянням прямолінійного руху. В проекції на вісь Ох із врахуванням того, що повна деформація пружини складає , рівняння матиме вигляд

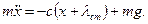
Врахувавши, що , одержимо

.

Після ділення на масу m матимемо

,

де .

Рівняння такого виду можна одержати, спрямувавши вісь Ох на рис. 2.2 вгору, або задавши довільне положення точки М, яке відповідатиме розтягу пружини. Вигляд рівняння при цьому не зміниться.

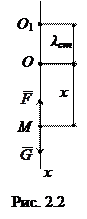Одержане рівняння є диференціальним рівнянням вільних коливань при відсутності опору. Його розв’язок згідно теорії диференціальних рівнянь у випадку, коли k² > 0, має вигляд

,

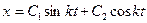де С₁ і С₂ - сталі інтегрування, які знаходяться з початкових умов.

Початкові умови задають відхилення точки від положення рівноваги і її швидкість в початковий момент часу:

при

Підставивши початкову умову для координати в розв’язок, одержимо: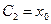. Для використання початкової умови візьмемо похідну по часу від розв’язку

.

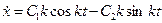Підставивши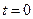і 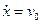, знайдемо: 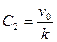, тоді розв’язок диференціального рівняння прийме вигляд

.

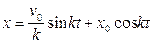Як видно з розв’язку, точка М буде рухатись при дії сили пружності , коли хоча б одна із початкових умов не дорівнює нулю. Отже, матеріальну точку необхідно вивести з положення рівноваги, розтягнувши (стиснувши) пружину або різким поштовхом надавши їй початкової швидкості. Рух почнеться і в тому випадку, коли встановити тіло на недеформованій пружині. При цьому для рис. 2.2 початкове відхилення x₀ = -λ_ст, оскільки відлік координати x ведеться від точки О положення статичної рівноваги тіла.

Одержаний розв’язок називається першою формою розв’язку диференціального рівняння вільних коливань при відсутності опору. При аналізі коливань зручніше користуватись другою або амплітудною формою розв´язку рівняння, яку можна одержати, скориставшись відомим з математики співвідношенням

де ; .

Тоді розв’язок матиме вигляд

Коливання, які виконує матеріальна точка по наведеному закону, називаються гармонічними. Графіком таких коливань буде синусоїда з амплітудою А і початковою фазою a. Рух точки повністю повторюється через проміжок часу , який називається періодом коливань. Із врахуванням періодичності тригонометричної функції

π; .

Величина ν, обернена періоду , називається частотою коливань

,

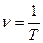а величина = 2π/T, що визначає число коливань, які точка здійснює за 2π секунд – круговою (або циклічною) частотою коливань.

Отже, кругова частота і період коливань визначаються лише масою точки і жорсткістю пружини і не залежать від початкових умов.

Амплітуда А і початкова фаза a в амплітудній формі розв'я­зку також є сталими інтегрування і знаходяться з початкових умов. Вирази для амплітуди і фази коливань мають вигляд

; .

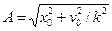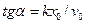З наведених виразів видно, що амплітуда і початкова фаза коливань залежать від початкових умов.