Приклади знаходження роботи
 1. Робота сили ваги. Нехай точка М, на яку діє сила ваги
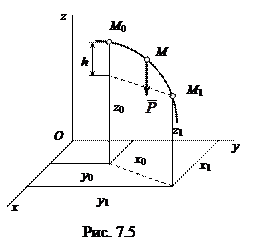
1. Робота сили ваги. Нехай точка М, на яку діє сила ваги 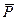 , переміщується з положення M0 (x0, y0, z0) в положення M1 (x1, y1, z1). Виберемо координатні осі так, щоб вісь Oz була спрямована вертикально вгору (рис. 7.5). Тоді Px = 0, Py = 0, Pz = -P. Після підстановки цих виразів в аналітичний вираз для елементарної роботи, одержимо, врахувавши, що змінною інтегрування є z:
, переміщується з положення M0 (x0, y0, z0) в положення M1 (x1, y1, z1). Виберемо координатні осі так, щоб вісь Oz була спрямована вертикально вгору (рис. 7.5). Тоді Px = 0, Py = 0, Pz = -P. Після підстановки цих виразів в аналітичний вираз для елементарної роботи, одержимо, врахувавши, що змінною інтегрування є z:
 .
.
Якщо точка М0 знаходиться вище, ніж М1, то z0 - z1 = h, де h – вертикальне переміщення точки; якщо ж точка М0 нижче точки М1, то z0 - z1 = -(z1 - z0) = -h.
Остаточно одержимо
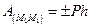 .
.
Отже, робота сили ваги дорівнює узятому зі знаком плюс або мінус добутку модуля сили на вертикальне переміщення точки її прикладання. Робота буде додатною, якщо початкова точка вище конечної, і від’ємною, якщо початкова точка нижче конечної.
Із одержаного результату випливає, що робота сили ваги не залежить від виду тієї траєкторії, по якій переміщується точка її прикладання. Сили, які мають таку властивість, називаються потенціальними.
У випадку механічної системи робота сили ваги визначиться додаванням робіт точок, що складають систему. Для механічної системи та твердого тіла вираз для роботи сили ваги має вигляд
А=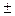 РhС,
РhС,
де Р – вага системи або тіла, а hС – вертикальне переміщення центру мас.
 2. Робота сили тертя. Розглянемо точку, яка рухається по шорсткій криволінійній поверхні (рис. 7.6). Сила тертя, яка діє на точку, дорівнює по модулю fN , де f – коефіцієнт тертя, а N – нормальна реакція поверхні. Направлена сила тертя протилежно переміщенню точки. Отже
2. Робота сили тертя. Розглянемо точку, яка рухається по шорсткій криволінійній поверхні (рис. 7.6). Сила тертя, яка діє на точку, дорівнює по модулю fN , де f – коефіцієнт тертя, а N – нормальна реакція поверхні. Направлена сила тертя протилежно переміщенню точки. Отже
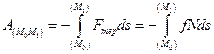 .
.
Якщо сила тертя є постійною величиною, то 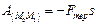 , де s – довжина дуги кривої М0М1, по якій переміщується точка.
, де s – довжина дуги кривої М0М1, по якій переміщується точка.
Таким чином, робота сили тертя при ковзанні завжди від’ємна.
 3. Робота сил, які прикладені до тіла, що обертається. Елементарна робота сили
3. Робота сил, які прикладені до тіла, що обертається. Елементарна робота сили 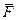 прикладена до тіла (рис. 7.7), дорівнює
прикладена до тіла (рис. 7.7), дорівнює
 dA =
dA = ,
,
оскільки ds = hd , де
, де 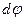 – елементарний кут повороту тіла.
– елементарний кут повороту тіла.
Але добуток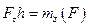 . Будемо називати величину
. Будемо називати величину 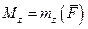 крутним моментом. Тоді одержимо
крутним моментом. Тоді одержимо
dA =Mzd .
.
Отже, елементарна робота дорівнює добутку крутного моменту на елементарний кут повороту.
При повороті на конечний кут φ1 робота: А = , а у випадку постійного моменту: А =
, а у випадку постійного моменту: А =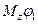 .
.
Визначимо також потужність при обертанні
N = dA/dt = Мzdφ/dt = Mzω.
Отже, при дії сил на тіло, яке обертається, при тій же самій потужності крутний момент буде тим більшим, чим менша кутова швидкість.
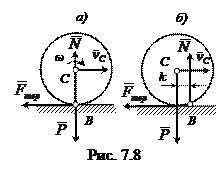
3. Робота тертя кочення. Тертям кочення називається опір, що виникає при коченні тіла по нерухомій поверхні. В теоретичній механіці розглядаються абсолютно тверді тіла (які не деформуються). Тому при коченні колеса радіусом R по нерухомій поверхні лінія дії нормальної реакції поверхні проходить через центр мас С (рис. 7.8, а). Але на практиці через деформацію поверхонь нормальна реакція зміщується від вказаного напрямку на величину k, яка називається коефіцієнтом тертя кочення (рис. 7.8, б). При цьому пара сил
поверхні проходить через центр мас С (рис. 7.8, а). Але на практиці через деформацію поверхонь нормальна реакція зміщується від вказаного напрямку на величину k, яка називається коефіцієнтом тертя кочення (рис. 7.8, б). При цьому пара сил  -
- , момент якої M = kN, створює опір коченню. Тоді при коченні колеса
, момент якої M = kN, створює опір коченню. Тоді при коченні колеса
 dAкоч = -kN dφ = -
dAкоч = -kN dφ = - NdsC,
NdsC,
де dsC – елементарне переміщення центру мас С колеса. Якщо N = const, то повна робота сил опору коченню
Aкоч = -kN φ1 = - NsC.
NsC.
З викладеними в лекції питаннями можна більш детально ознайомитись за підручником С.М. Тарга [1]: моменти кількості руху матеріальної точки та механічної системи – с. 204-205, 290; кінетичний момент тіла, яке обертається навколо нерухомої осі – с. 291; теорема про зміну моменту кількості руху точки – с. 205-206; теорема про зміну головного моменту кількостей руху системи (теорема моментів) – с. 292-293; закон збереження головного моменту кількостей руху та його прояви – с. 294-295; робота сили, потужність – с. 208-209; приклади знаходження роботи – с. 210-213, 305-307.