Економічна постановка задачі, її математична модель.
Серед задач лінійного програмування можна виділити деякі види задач, моделі яких мають певну специфіку. Прикладом такої задачі є, так звана, транспортна задача.
Постановка транспортної задачі пов'язана з визначенням такого плану перевезення вантажу від постачальників до споживачів, при якому загальні транспортні витрати були б найменшими за умови, що мають бути задоволені потреби споживачів. Можливості кожного постачальника, а також потреби кожного споживача вважаються відомими.
Для побудови економіко-математичної моделі транспортної задачі введемо позначення: 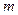 – кількість постачальників;
– кількість постачальників; 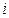 – номер постачальника,
– номер постачальника,  ;
; 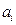 – кількість вантажу в
– кількість вантажу в 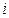 -го постачальника,
-го постачальника,  ;
; 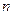 – кількість споживачів;
– кількість споживачів; 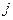 – номер споживача,
– номер споживача, 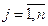 ;
;  – потреби
– потреби 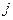 -го споживача,
-го споживача, 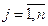 ;
; 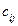 – вартість перевезення одиниці вантажу від
– вартість перевезення одиниці вантажу від 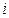 -го постачальника до
-го постачальника до 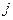 -го споживача,
-го споживача,  ,
, 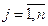 . Змінні моделі
. Змінні моделі 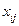 означають кількість вантажу, який перевозиться від
означають кількість вантажу, який перевозиться від 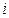 -го постачальника до
-го постачальника до 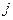 -го споживача. Тоді умову задачі можна записати у вигляді наступної таблиці (матриці планування):
-го споживача. Тоді умову задачі можна записати у вигляді наступної таблиці (матриці планування):
| Постачальники | Споживачі | Запаси | ||||||
| … | 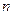
| |||||||
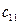
| 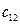
| … | 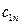
| 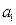
| ||||

| 
| 
| ||||||
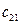
| 
| … | 
| 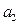
| ||||

| 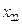
| 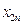
| ||||||
| … | … | … | … | … | … | |||
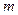
| 
| 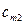
| … | 
| 
| |||
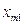
| 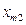
| 
| ||||||
| Потреби | 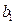
| 
| … | 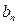
|
Загальні транспортні витрати  обчислюються за формулою:
обчислюються за формулою:
 .
.
Згідно з критерієм оптимальності ці витрати мають бути мінімальними, тому цільова функція транспортної задачі прямує до мінімуму:
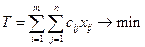 (13)
(13)
План перевезень 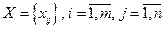 має задовольняти умови:
має задовольняти умови:
– загальний обсяг вантажу, який вивозиться від кожного постачальника, повинен бути рівним його запасу:
 (14)
(14)
– обсяг вантажу, який надходить кожному споживачеві, повинен бути рівним його потребам:
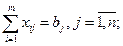 (15)
(15)
– обсяги вантажу на кожному з маршрутів мають бути невід'ємними:
 . (16)
. (16)
Система умов (13) – (16) є математичною моделлю транспортної задачі.
Якщо в транспортній задачі кількість продукції усіх постачальників рівна загальному попиту всіх споживачів, тобто
 , (17)
, (17)
то таку транспортну задачу називають збалансованою або закритою. Якщо ж така умова не виконується, то ТЗ називається незбалансованою або відкритою.
Теорема. Будь-яка збалансована транспортна задача має розв’язок.
Для того, щоб розв’язати незбалансовану транспортну задачу спочатку необхідно її збалансувати. Можливі два випадки:
1. Загальні потреби споживачів більші від загального запасу продукції постачальників:  .
.
У такому разі ТЗ нерозв’язна через наявність дефіциту продукції. Для розв’язування такої задачі необхідно ввести фіктивного постачальника, який забезпечить 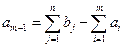 одиниць продукції. Фіктивні поставки продукції означають дефіцит продукції у
одиниць продукції. Фіктивні поставки продукції означають дефіцит продукції у 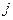 -го споживача.
-го споживача.
2. Загальна кількість продукції постачальників більша від загального попиту споживачів:  .
.
Для розв’язування такої задачі необхідно ввести фіктивного споживача.
Фіктивні поставки продукції  означають залишок продукції у
означають залишок продукції у 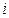 -го постачальника.
-го постачальника.
І в першій, і в другій ситуації норми витрат на доставку продукції рівні нулю.
Математична модель транспортної задачі (13)–(16) є задачею лінійного програмування. Специфіка цієї задачі полягає у системі її обмежень, яка є системою з  лінійних рівнянь відносно
лінійних рівнянь відносно 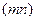 змінних
змінних 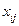 . Виявляється, що дана система складається з
. Виявляється, що дана система складається з  лінійно незалежних рівнянь. Тому опорному розв’язку відповідатиме
лінійно незалежних рівнянь. Тому опорному розв’язку відповідатиме  лінійно незалежних векторів та кількість базисних маршрутів
лінійно незалежних векторів та кількість базисних маршрутів 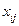 для будь-якої транспортної задачі дорівнює
для будь-якої транспортної задачі дорівнює  .
.
Опорний план транспортної задачі називається невиродженим, якщо у ньому точно  додатних компонент
додатних компонент 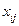 .
.
Для розв’язування ТЗ можна використовувати симплекс-метод, проте зважаючи на специфіку ТЗ, можна застосовувати більш ефективний алгоритм – метод потенціалів.
Алгоритм методу потенціалів складається з таких етапів:
1. Визначення типу ТЗ (збалансована чи незбалансована). У другому випадку – збалансувати.
2. Побудова першого опорного плану ТЗ.
3. Визначення потенціалів опорного плану ТЗ.
4. Перевірка опорного плану ТЗ на оптимальність. Якщо умова оптимальності не виконується, то повторити дії, починаючи з п.3.
1. Як збалансувати ТЗ було розглянуто раніше. Переходимо до п.2.
2. Для побудови початкового опорного плану транспортної задачі існує кілька методів: північно-західного кута; мінімальної вартості; подвійної переваги, метод Фогеля та інші. Побудову опорного плану зручно подавати у вигляді таблиці, в якій постачальники продукції визначаються рядками, а споживачі - стовпчиками.