Понятие об интегральном преобразовании Ханкеля
Пусть функция  определена в области
определена в области  и удовлетворяет в ней следующим условиям.
и удовлетворяет в ней следующим условиям.
1. 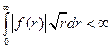 , т.е. несобственный интеграл сходится.
, т.е. несобственный интеграл сходится.
2. Функция  имеет конечное число максимумов и минимумов в любом конечном промежутке области
имеет конечное число максимумов и минимумов в любом конечном промежутке области  .
.
3. В любом таком промежутке функция  имеет конечное число конечных разрывов и не имеет бесконечных.
имеет конечное число конечных разрывов и не имеет бесконечных.
Перечисленные условия являются достаточными для того, чтобы при  имели место формулы [2]
имели место формулы [2]
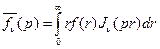 , (2.1)
, (2.1)
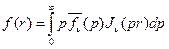 . (2.2)
. (2.2)
В точках разрыва функции  последний интеграл принимает значения
последний интеграл принимает значения 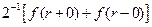 .
.
Функция 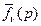 называется трансформантой Ханкеля функции
называется трансформантой Ханкеля функции  . Вторая формула называется формулой обращения. Формулы (2.1) и (2.2) определяют соответственно прямое и обратное преобразование Ханкеля.
. Вторая формула называется формулой обращения. Формулы (2.1) и (2.2) определяют соответственно прямое и обратное преобразование Ханкеля.
В дальнейшем нам потребуется следующие два свойства преобразования Ханкеля.
Свойство (2.1)
 . (2.3)
. (2.3)
Свойство(2.2)
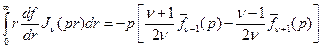 . (2.4)
. (2.4)
Эти свойства могут быть доказаны в предположении, что  и
и 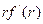 при
при 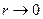 являются величинами порядка
являются величинами порядка 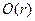 , а при
, а при 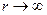 ограничены, т.е. являются величинами порядка
ограничены, т.е. являются величинами порядка  и, кроме того,
и, кроме того, 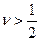 при доказательстве второго свойства.
при доказательстве второго свойства.
Доказательство свойства (2.1) Применим дважды правило интегрирования по частям к интегралу

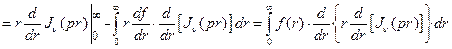 .
.
Интеграл в левой части соотношения (2.3) запишем в иной форме:
 .
.
В выражении в фигурных скобках перейдем к переменной 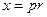 . В этом случае
. В этом случае
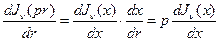
 .
.
Следовательно,
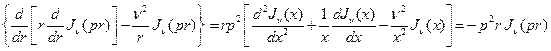
на основании (1.7).
Поэтому рассматриваемый интеграл согласно (2.1) равен
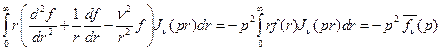 .
.
Первое свойство доказано.
Доказательство свойства (2.2) Также основано на применение к интегралу в соотношении (2.4) правила интегрирования по частям.
В процессе доказательства необходимо перейти к переменной 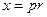 в подынтегральном выражении и воспользоваться рекуррентными соотношениями (1.8) и (1.9).
в подынтегральном выражении и воспользоваться рекуррентными соотношениями (1.8) и (1.9).
Отметим важные для дальнейшего частные случаи свойств (2.1) и (2.2). Положив в соотношении (2.3) 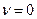 , получим
, получим
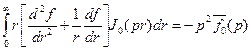 . (2.5)
. (2.5)
В соотношении (2.4) положим 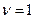 . Тогда будем иметь
. Тогда будем иметь
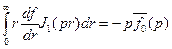 . (2.6)
. (2.6)