Для многослойных оснований с гладкими слоями
Под первой граничной задачей условимся понимать задачу об определении напряжений и перемещений в многослойном основании по заданным на его верхней границе нормальным напряжениям  . (Напомним, что касательные напряжения на граничных поверхностях любого слоя равны нулю в основании с гладкими слоями). Если же на верхней границе основания заданы нормальные перемещения
. (Напомним, что касательные напряжения на граничных поверхностях любого слоя равны нулю в основании с гладкими слоями). Если же на верхней границе основания заданы нормальные перемещения  , то задачу определения напряженно-деформированного состояния основания будем называть второй граничной задачей.
, то задачу определения напряженно-деформированного состояния основания будем называть второй граничной задачей.
В том случае, когда на части верхней границы основания с гладкими слоями заданы нормальные напряжения  , а на оставшейся части перемещения
, а на оставшейся части перемещения  , то задачу об определении напряженно-деформированного состояния многослойного основания будем называть смешанной граничной задачей.
, то задачу об определении напряженно-деформированного состояния многослойного основания будем называть смешанной граничной задачей.
Во всех этих задачах на нижней границе основания должно выполняться условие 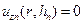 или, что то же,
или, что то же, 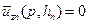 . Выражая последовательно через
. Выражая последовательно через  и
и 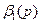 функции
функции  и
и 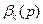
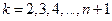 при помощи рекуррентных соотношений (4.3), (4.4), найдем, что функция
при помощи рекуррентных соотношений (4.3), (4.4), найдем, что функция 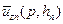 линейна и однородна относительно
линейна и однородна относительно 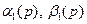 :
:
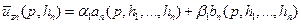 .
.
Функции 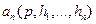 ,
,  , как это следует из способа их построения, зависят от толщин всех слоев основания и модулей упругости их, но не зависят ни от
, как это следует из способа их построения, зависят от толщин всех слоев основания и модулей упругости их, но не зависят ни от  , ни от
, ни от 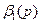 . Из требования
. Из требования  вытекает, что
вытекает, что
 . (5.1)
. (5.1)
Функция 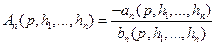 , по сказанному, не зависит от
, по сказанному, не зависит от 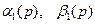 , т. е. не зависит от способа нагружения основания. Поэтому она в принципе может быть определена до решения какой-либо граничной задачи. Ниже будет указан эффективный способ нахождения функции
, т. е. не зависит от способа нагружения основания. Поэтому она в принципе может быть определена до решения какой-либо граничной задачи. Ниже будет указан эффективный способ нахождения функции 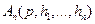 .
.
Выясним физический смысл этой функции. Согласно формулам (4.7) и (5.1) перемещения точек верхней границы основания (осадка поверхности основания) могут быть для заданной нагрузки найдены следующим образом:
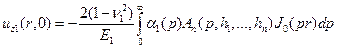 . (5.2)
. (5.2)
Вообразим себе несколько различных многослойных оснований, которые нагружены одинаковым образом. У этих оснований будут различными функции 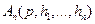 и одинаковыми
и одинаковыми  . Форма деформированной границы будет, вообще говоря, неодинаковой для различных оснований (при одинаковых материалах их верхних слоев) из-за того, что функции
. Форма деформированной границы будет, вообще говоря, неодинаковой для различных оснований (при одинаковых материалах их верхних слоев) из-за того, что функции 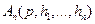 у сравниваемых оснований различны. Отсюда следует, что функция
у сравниваемых оснований различны. Отсюда следует, что функция 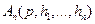 полностью определяет податливость верхней границы основания нормальной нагрузке. В силу этого будем функцию
полностью определяет податливость верхней границы основания нормальной нагрузке. В силу этого будем функцию 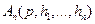 называть функцией податливости многослойного основания.
называть функцией податливости многослойного основания.
Знание функции податливости существенно облегчает решение всех граничных задач для многослойного основания. Особенно эффективно использование функций податливости для решения 1 и 2 граничных задач. В самом деле, одна из пары функций 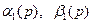 определяется из соотношения (5.1). Все остальные
определяется из соотношения (5.1). Все остальные 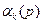 и
и 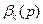 находятся при помощи рекуррентных формул (4.3) ‑ (4.4), а напряжения и перемещения определяются по формулам (3.16) и (2.2) при помощи найденных
находятся при помощи рекуррентных формул (4.3) ‑ (4.4), а напряжения и перемещения определяются по формулам (3.16) и (2.2) при помощи найденных  и
и 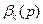 .
.
Ввиду большого теоретического и прикладного значения функций податливости заслуживают внимания любые эффективные способы построения их. Изложим один из них [4]. Пусть имеем  -1-слойное основание, нумерация слоев в котором начинается с цифры 2. Предположим, что для такого основания функция податливости
-1-слойное основание, нумерация слоев в котором начинается с цифры 2. Предположим, что для такого основания функция податливости  известна. Согласно (5.1) имеем
известна. Согласно (5.1) имеем
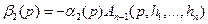 .
.
Положим на поверхность  -1-слойного основания гладкий слой, которому присвоим номер 1. Получим
-1-слойного основания гладкий слой, которому присвоим номер 1. Получим  -слойное основание. Выражая теперь в последнем равенстве
-слойное основание. Выражая теперь в последнем равенстве 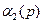 и
и 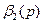 через и
через и  и
и 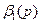 при помощи рекуррентных формул (4.3), (4.4) и совершая замену
при помощи рекуррентных формул (4.3), (4.4) и совершая замену  , получим после очевидных преобразований рекуррентную формулу
, получим после очевидных преобразований рекуррентную формулу
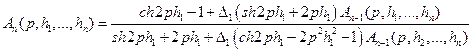 . (5.3)
. (5.3)
В качестве примера определим функции  и
и  для однослойного основания и полупространства. Из формулы (5.2) следует, что для абсолютно жесткого основания
для однослойного основания и полупространства. Из формулы (5.2) следует, что для абсолютно жесткого основания 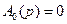 , так как при любом нагружении такого основания
, так как при любом нагружении такого основания  . Полагая в формуле (5.3)
. Полагая в формуле (5.3)  ,
, 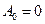 , получаем функцию податливости для однослойного основания
, получаем функцию податливости для однослойного основания
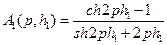 .
.
Неограниченно увеличивая  , в пределе получим функцию податливости для полупространства
, в пределе получим функцию податливости для полупространства
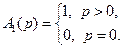
Функция податливости в окончательных результатах всегда находится под знаком интеграла. Изменение значений подынтегральной функции в конечном и даже счетном множестве точек, как известно [1], не сказывается на значении интеграла. Поэтому в дальнейшем считаем функцию  непрерывной, т.е.
непрерывной, т.е.
 .
.
Полученное выражение для  согласуется с (3.18) и (5.1).
согласуется с (3.18) и (5.1).
Установим важнейшие свойства функции податливости 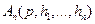 . Заметим, что функции
. Заметим, что функции  и
и  непрерывны, ограничены, знакопостоянны, любое число раз дифференцируемы в интервале
непрерывны, ограничены, знакопостоянны, любое число раз дифференцируемы в интервале 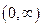 . При
. При  обе стремятся к 1. Предполагая, что такими же свойствами обладает функция
обе стремятся к 1. Предполагая, что такими же свойствами обладает функция  , при помощи соотношения (5.3) легко установить, что аналогичными свойствами обладает и функция
, при помощи соотношения (5.3) легко установить, что аналогичными свойствами обладает и функция 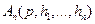 . Таким образом, методом полной математической индукции обнаружим, что
. Таким образом, методом полной математической индукции обнаружим, что
1. Функция 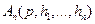 ,
, 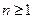 , непрерывна, ограничена, дифференцируема, знакопостоянна в интервале
, непрерывна, ограничена, дифференцируема, знакопостоянна в интервале 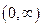 .
.
2. 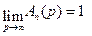
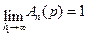 при
при 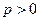 .
.
3. При 

4. 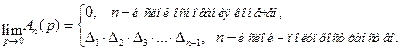
5  .
.
При доказательстве свойств функции податливости необходимо пользоваться следующими свойствами гиперболических функций:
1) 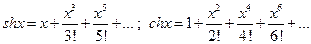 ;
;
2) при 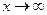
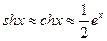 .
.
Отсюда, в частности, следует, что
 .
.
Знак равенства возможен лишь при 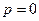 .
.