НОРМАЛЬНЫЙ ЗАКОН РАСПРЕДЕЛЕНИЯ И ЕГО ПРИМЕНЕНИЕ
Нормальный закон распределения играет важнейшую роль в применении численных методов в психологии. Он лежит в основе измерений, разработки тестовых шкал, методов проверки гипотез.
История применения закона нормального распределения в социальных и биологических науках начинается, по-видимому, с работы бельгийского ученого А. Кетле «Опыт социальной физики» (1835 г.). В ней он доказывал, что такие явления, как продолжительность жизни, возраст вступления в брак и появления первого ребенка и т. д., подчиняются строгой закономерности. Она проявляется в том, что чаще всего встречаются средние значения соответствующих показателей, и чем больше отклонение от этой средней величины, тем реже встречаемость таких отклонений. Одинаковые отклонения от среднего в меньшую и в большую сторону встречаются одинаково реже, чем среднее значение. Эту закономерность он назвал «законом уклонения от средней величины». В его исследованиях, и позднее — в исследованиях англичанина Ф. Галь-тона, было доказано, что распределение частот встречаемости любого демографического (продолжительность жизни и пр.) или антропометрического (рост, вес и пр.) показателя, измеренного на большой выборке людей, имеет одну и ту же «колоколо-
Частота
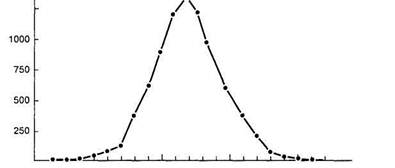
152 165 178 191 РОСТ, CM
Рис. 5.1. Полигон частот для роста 8585 взрослых людей, родившихся в Англии в XIX в.1
 ' Гласе Дж., Стенли Дж. Статистические методы в педагогике и психологии. М., 1976. С. 98.
' Гласе Дж., Стенли Дж. Статистические методы в педагогике и психологии. М., 1976. С. 98.
ЧАСТЬ I. ОСНОВЫ ИЗМЕРЕНИЯ И КОЛИЧЕСТВЕННОГО ОПИСАНИЯ ДАННЫХ

|

|
образную» форму (см. рис. 5.1). Форма таких распределений может быть описана математической формулой, которую предложил еще в XVIII веке математик де Муавр.
Де Муавр решал следующую задачу. Предположим, монета в азартной игре подбрасывается 10 раз, и каждый раз она может с равным успехом выпасть «орлом» или «решкой». Какова вероятность того, что в результате этой игры выпадет 0 «орлов», или 1 «орел», ..., 10 «орлов»? Сложные вычисления дают математически точное решение такой задачи (рис. 5.2). А если игра состоит из 100 подбрасываний монеты, или 1000? Де Муавру удалось доказать, что уравнение кривой, соединяющей вершины отрезков на рис. 5.2, для данного случая или для любой другой подобной задачи имеет следующую формулу:

(5.1)
где/(х,) — высота подъема кривой, е — основание натурального логарифма (примерно 2,718), л — число «пи» (примерно 3,14), Ми а — среднее и стандартное отклонения для переменной х„ которые определяют положение кривой на числовой оси и задают ее размах. Эта формула и соответствующая ей кривая (см. рис. 5.2) впоследствии получили название закона нормального распределения.
Итак, исход азартной игры, и продолжительность жизни, и рост человека — все это случайные события, частота (или вероятность) встречаемости которых подчинена закону нормального распределения. А. Кетле объяснял это существованием «идеала» человеческой природы, которому соответствуют средние значения различных пока-
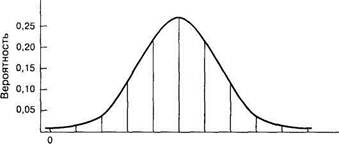
1 2 3 4 5 6:
Число «орлов»
Рис. 5.2. График распределения вероятностей выпадения «орлов» в игре с 10 подбрасываниями монеты и кривая нормального распределения
ГЛАВА 5. НОРМАЛЬНЫЙ ЗАКОН РАСПРЕДЕЛЕНИЯ И ЕГО ПРИМЕНЕНИЕ
зателей. Ф. Гальтон, двоюродный брат Ч.Дарвина, проявление нормального закона рассматривал в связи с биологической изменчивостью, наследственностью и отбором. В дальнейшем трудами Ф. Гальтона и его последователей было доказано, что и психологические особенности, например способности, подчиняются нормальному закону. Поэтому дальнейшее развитие измерительного подхода в психологии и статистического аппарата проверки гипотез происходило на базе этого общего закона.
Подведем важный итог этого краткого исторического экскурса. Начиная со второй половины XIX столетия измерительные и вычислительные методы в психологии разрабатываются на основе следующего принципа. Если индивидуальная изменчивость некоторого свойства есть следствие действия множества причин, то распределение частот для всего многообразия проявлений этого свойства в генеральной совокупности соответствует кривой нормального распределения. Это и есть закон нормального распределения.
Закон нормального распределения имеет целый ряд очень важных следствий, к которым мы не раз еще будем обращаться. Сейчас же отметим, что если при изучении некоторого свойства мы произвели его измерение на выборке испытуемых и получили отличающееся от нормального распределение, то это значит, что либо выборка нерепрезентативна генеральной совокупности, либо измерения произведены не в шкале равных интервалов.
НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ КАК СТАНДАРТ
|

|
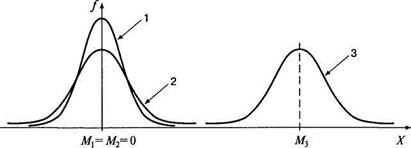
Каждому психологическому (или шире — биологическому) свойству соответствует свое распределение в генеральной совокупности. Чаще всего оно является нормальным и характеризуется своими параметрами: средним (М) и стандартным отклонением (о). Только эти два значения отличают друг от друга бесконечное множество нормальных кривых, одинаковой формы, заданной уравнением (5.1). Среднее задает положение кривой на числовой оси и выступает как некоторая исходная, нормативная величина измерения. Стандартное отклонение задает ширину этой кривой, зависит от единиц измерения и выступает как масштаб измерения (рис. 5.3).
ЧАСТЬ I. ОСНОВЫ ИЗМЕРЕНИЯ И КОЛИЧЕСТВЕННОГО ОПИСАНИЯ ДАННЫХ
Все многообразие нормальных распределений может быть сведено к одной кривой, если применить ^-преобразование (по формуле 4.8) ко всем возможным измерениям свойств. Тогда каждое свойство будет иметь среднее 0 и стандартное отклонение 1. На рис. 5.4 построен график нормального распределения для М= 0 и а = 1. Это и есть единичное нормальное распределение, которое используется как стандарт — эталон. Рассмотрим его важные свойства.

Последнее свойство объясняет название единичное нормальное распределение и имеет исключительно важное значение. Благодаря этому свойству площадь под кривой интерпретируется как вероятность, или относительная частота. Действительно, вся площадь под кривой соответствует вероятности того, что признак примет любое значение из всего диапазона его изменчивости (от -оо до +оо). Площадь под единичной нормальной кривой слева или справа от нулевой точки равна 0,5. Это соответствует тому, что половина генеральной совокупности имеет значение признака больше 0, а половина — меньше 0. Относительная частота встречаемости в генеральной совокупности значений признака в диапазоне от Z до Zi равна площади под кривой, лежащей между соответствующими точками. Отметим еще раз, что любое нормальное распределение может быть сведено к единичному нормальному распределению путем z-преобразования.

|
| 13,59% 2,14% 0,13% |
95,44%
 99,72%
99,72%
 Рис. 5.4. Стандартное нормальное распределение
Рис. 5.4. Стандартное нормальное распределение
ГЛАВА 5. НОРМАЛЬНЫЙ ЗАКОН РАСПРЕДЕЛЕНИЯ И ЕГО ПРИМЕНЕНИЕ
Таким образом:
□ если х, имеет нормальное распределение со средним М и стандартным отклонением о, то z = (х— Мх)/а характеризуется единичным нормальным распределением со средним 0 и стандартным отклонением 1;
П площадь между х, и х2 в нормальном распределении со средним Мх и стандартным отклонением о равна площади между Z = (xl — Мх)/а и Z2 = (x2 — Мх)/а в единичном нормальном распределении.
Итак, наиболее важным общим свойством разных кривых нормального распределения является одинаковая доля площади под кривой между одними и теми же двумя значениями признака, выраженными в единицах стандартного отклонения.
Полезно помнить, что для любого нормального распределения существуют следующие соответствия между диапазонами значений и площадью под кривой:
М±а соответствует«68% (точно — 68,26%) площади;
М±2осоответствует =95% (точно — 95,44%) площади;
М±3а соответствует =100%(точно — 99,72%) площади.
Единичное нормальное распределение устанавливает четкую взаимосвязь стандартного отклонения и относительного количества случаев в генеральной совокупности для любого нормального распределения. Например, зная свойства единичного нормального распределения, мы можем ответить на следующие вопросы. Какая доля генеральной совокупности имеет выраженность свойства от — о до +1о? Или какова вероятность того, что случайно выбранный представитель генеральной совокупности будет иметь выраженность свойства, на За превышающую среднее значение? В первом случае ответом будет 68,26% всей генеральной совокупности, так как от — 1 до +1 содержится 0,6826 площади единичного нормального распределения. Во втором случае ответ: (100-99,72)/2 = 0,14%.
Полезно знать, что если распределение является нормальным, то:
90%всех случаев располагается в диапазоне значений М+ 1,64а;
95%всех случаев располагается в диапазоне значений М± 1,96с;