Группа 3. Аксиомы конгруэнтности
Группы аксиом 1–3 позволяют доказать основные свойства отношения конгруэнтности между геометрическими фигурами, определить понятие движения в геометрии и установить признаки конгруэнтности геометрических фигур. Первая аксиома этой группы содержит два требования, а четвертая– три.
13. Пусть даны отрезок АВ а также прямая а/ и точка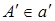 
. 
точка 
с заданной стороны относительно точки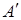 
такая, что отрезок АВ конгруэнтен отрезку 
(обозначим это 
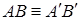), требуется также, чтобы 
.
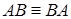14. 
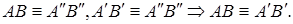
15. Пусть АВ и ВС – отрезки на прямой 
, АВ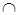
ВС=В, тогда
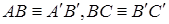и 
лежит между 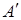и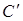 
.
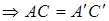16. Пусть Ð
есть угол с вершиной О. Для любой точки 
и любого выходящего из нее луча 
можно построить в заданной плоскости, инцидентной 
, по любую сторону от один и только один, второй луч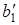 
такой, что Ð
.
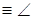
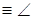
Требуется также, чтобы Ð(угол конгруэнтен самому себе) и Ð
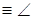
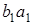
17. Пусть даны два треугольника АВС и 
таких, что 
, 
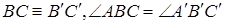, тогда 
.
На основании аксиом конгруэнтности вводятся понятия прямого угла, смежных и вертикальных конгруэнтных углов, операции сравнения углов и отрезков. Отрезок АВ больше отрезка СD, обозначается АВ>СD, если при совмещении точек А и С и откладывании точек В и D по одну сторону от точки А на некоторой прямой, точка D будет лежать между
А и С.
В этой группе аксиом доказываются три признака конгруэнтности треугольников, свойства равнобедренных и равносторонних треугольников и т.д. Справедлива также теорема о внешнем угле треугольника в слабом варианте (известная еще Евклиду).