ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОГО ФОРМАЛИЗМА ДЛЯ ФИЛОЛОГОВ

Министерство образования Российской Федерации

 

 

НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

 

В. А. СЕЛЕЗНЕВ

 

ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОГО ФОРМАЛИЗМА ДЛЯ ФИЛОЛОГОВ

 

Рекомендовано Редакционно–издательским советом университета для студентов I курса ФГО (направление “Филология”)

 

 

НОВОСИБИРСК

СЕЛЕЗНЕВ В. А. Элементы математического формализма для филологов:Учеб. пособие. – Новосибирск: Изд–во НГТУ, 2000 г., 68 с.

 

Настоящее пособие подготовлено для студентов I курса филологического отделения факультета гуманитарного образования и содержит разделы: математический формализм, свойства аксиоматических систем.

Объем пособия соответствует краткому семестровому курсу «введение в математику для филологов», читаемому автором в течение нескольких лет.

Цель пособия – познакомить филологов с идеями математического формализма на основе традиционных аксиоматических теорий и классических моделей.

Автор выражает благодарность студентам I курса, оказавшим помощь в подготовке макета.

 

 

Список библ. 12 названий.

Рецензент К. Н. Пономарев, д–р физ.–мат. наук, проф.

Работа выполнена на кафедре высшей математики.

 

 

© Новосибирский Государственный

Технический Университет, 2000 г.

 

Оглавление

Введение............................................................................................................................................. 5

ГЛАВА I........................................................................................................................................... 10

МАТЕМАТИЧЕСКИЙ ФОРМАЛИЗМ......................................................................................... 10

§ 1. О понятии действительных чисел................................................................................. 10

1.1. Формализм натуральных чисел.................................................................................. 10

1.2. Операции, определяющие формирование множества рациональных чисел...... 12

1.3. Аксиоматика рациональных чисел............................................................................ 14

1.4. Задачи, приводящие к расширению множества рациональных чисел................. 16

1.5. Аксиоматизация множества действительных чисел................................................ 17

1.6. О представлении действительных чисел.................................................................. 18

§ 2. Аксиоматическое обоснование евклидовой геометрии............................................. 18

2.1. О “Началах” Евклида.................................................................................................. 18

2.2. Аксиоматика Д. Гильберта(1862–1943)..................................................................... 20

2.3. Два недостатка аксиоматики Д. Гильберта............................................................... 26

§ 3. Структура векторного пространства............................................................................ 27

3.1. Модель направленных отрезков................................................................................. 27

3.2. Арифметическая модель векторного пространства................................................. 29

3.3. Абстрактное векторное пространство....................................................................... 31

3.4. Аксиомы скалярного произведения векторов.......................................................... 32

§ 4. Модель Вейля евклидовой геометрии.......................................................................... 34

4.1. Арифметизация трехмерного евклидова пространства........................................... 34

4.2. Многомерное арифметическое евклидово пространство........................................ 36

§ 5. Модель А. Пуанкаре плоскости Лобачевского............................................................ 37

5.1. Основные понятия модели А. Пуанкаре плоскости Лобачевского....................... 37

5.2. Основные факты в планиметрии Лобачевского...................................................... 40

5.3. О роли открытия неевклидовой геометрии.............................................................. 42

ГЛАВА II.......................................................................................................................................... 43

СВОЙСТВА АКСИОМАТИЧЕСКИХ СИСТЕМ........................................................................ 43

§ 6. Математические структуры и аксиоматические теории............................................. 43

6.1. Понятие отношений между объектами..................................................................... 43

6.2. Понятие математической структуры......................................................................... 44

6.3. Модель или реализация системы аксиом................................................................. 46

6.4. Формальная и содержательная аксиоматики. Теории и структуры...................... 46

6.5. Изоморфизм.................................................................................................................. 48

§ 7. Требования , предъявляемые к системам аксиом........................................................ 50

7.1. Непротиворечивость системы аксиом....................................................................... 50

7.2. Независимость аксиоматической системы............................................................... 51

7.3. Независимость аксиомы параллельности................................................................. 52

7.4. Дедуктивная полнота и категоричность системы аксиом....................................... 52

7.5. Историческая роль V постулата Евклида в развитии оснований математики.... 53

§ 8. Анализ текстовых парадоксов....................................................................................... 54

8.1. Языковые свойства имен объектов............................................................................ 54

8.2. Проблема выразимости............................................................................................... 55

8.3. Понятие искусственного языка................................................................................ 55

8.4. Понятие парадокса....................................................................................................... 56

8.5. “Ахиллес и черепаха”.................................................................................................. 56

8.6. Парадокс пустого множества..................................................................................... 57

8.7. Парадокс достижимости в натуральном ряде........................................................... 57

8.8. “Одно и то же, но по–разному”.................................................................................. 58

Заключение....................................................................................................................................... 59

Обозначения..................................................................................................................................... 62

ЛИТЕРАТУРА.................................................................................................................................. 63

Введение

Развитие информационных систем и компьютерных технологий открыло новые возможности в исследовании человеческого интеллекта. Цель такого исследования состоит в моделировании интеллекта и, в конечном счёте, автоматизации ряда процессов интеллектуальной деятельности.

Интеллект является процессом и продуктом мышления и отражает отношения объектов различной природы в виде мыслительных образов. Эти образы составляют субъективный информационный мир личности, а обмен информацией между людьми осуществляется посредством различных языковых систем. Знаковые или символьные языковые системы позволяют каждому индивидууму реализовать мысленную систему образов в виде языковых единиц – слов и их структурных образований – текстов.

Различают следующие три основные функции языка:

· отслеживание мысли (опорная функция);

· формирование умозаключений (логическая функция);

· средство общения (коммуникационная функция).

Такую роль языку отводил великий математик Леонард Эйлер (1707 – 1763). Он писал: “Язык нужен людям, чтобы они могли следить за своими мыслями и развивать их, а также общаться друг с другом”, ([1, с.282]).

Опорную функцию языка впервые систематически исследовал известный логик конца XIX в. Готлоб Фреге (1848 – 1925). Вот его слова: “Нам удаётся управлять нашим вниманием и направлять мысль в желательное для нас русло благодаря знакам. Когда мы воспроизводим знак, то мы тем самым создаём определённую опору нашей мысли, – определённый центр, вокруг которого возникают различные представления. Из этих представлений мы выбираем одно и опять фиксируем его с помощью знака. Так удаётся шаг за шагом проникнуть во внутренний мир наших представлений и двигаться в этом мире в нужном направлении. Чувственно–наглядное (в форме знаков) позволяет нам не потонуть в потоке восприятий и представлений, непрерывно захлёстывающих наше внимание”

Можно считать, что Фреге открыл акт и цикл процесса организации мыслительных образов в слова и тексты. Представим этот акт в виде схемы 0.

 

Тогда текст является итерацией, т.е. последовательной композицией таких актов.

Прежде чем сформулировать цели и задачи нашего пособия, приведём языковые понятия, при помощи которых формируется понятие текста.

 

Ф.1	Определение символьного или знакового языка
Знаковая или символьная система, используемая для такой организации структуры мыслительных образов, которая представляет информацию, называется символьным или знаковым языком

Пример 1

Система дискретных звуковых знаков есть общепринятое понятие человеческого языка, являющегося средством общения.

Пример 2

Система последовательностей двух символов 0 и 1 представляет язык числовых кодов: 110001, 100100100 и т.д.

Пример 3

Система знаков, представляющих музыкальные звуки, называется нотами.

 

Ф.2	Нотные знаки гаммы целых звуков одной октавы

 

Языковой способ коммуникации, то есть передачи информации, основан на композиции знаковых единиц – потоке слов, организованных в предложения – тексты.

 

 

Ф.3	Определение формального слова
Языковую знаковую или символьную единицу, представляющую мыслительный образ, назовём формальным словом

 

 

Ф.4	Определение формального предложения
Упорядоченное множество формальных слов, несущее в себе информацию законченного характера, назовём формальным предложением

 

Ф.5	Определение формального текста
Последовательность формальных предложений, синтезирующую информационный поток, назовём формальным текстом

 

Тексты, организованные в самостоятельные блоки, как это сделано выше, назовём файлами.

 

Ф.6	Определение файла
Текст

 

Файлы несут свой мыслительный образ, и поэтому их можно использовать для организации более сложных, нелинейных текстовых структур: каталогов, диаграмм, блок–схем и т.д. Пример – Схема 1, приведённая ниже. Ещё пример – синтезирование понятия символьного языка в виде блок–схемы:

Схема 1

Каждый предмет (литература, математика, экономика и т. д.) имеет свой язык. Разные модели одного предмета имеют разные языки, например:

· литературное произведение на русском и английском языках;

· геометрический и координатный языки в математических моделях;

· геометрическая и аналитическая теория интеграла и т. д.

Каждый из этих предметов и моделей является реализацией процесса мышления в виде языковой модели–текста. Поэтому текст можно считать основным продуктом интеллектуальной деятельности. Следовательно, исследование интеллектуального уровня и интеллектуальных функций – это исследование языковых продуктов.

Вывод

Сущность языковых систем состоит в том, что закономерности мыслительных процессов реализуются в законах организации текстовых структур.

Вопрос

Каковы закономерности знаковых систем, представляющих интеллектуальную продукцию в текстовой форме?

Ответ на этот вопрос не возможен без анализа современного научного направления, синтезированного исследованиями психологии, лингвистики, математики, физики информационных процессов и др. Остановимся кратко на избранных достижениях исследований языковых текстов.

В первой половине XX столетия исследования Эсту, Кондона и Ципфа завершились открытием статистического рангового распределения элементов словаря.

В чём суть этого открытия? Известно, что одни слова как знаковые единицы употребляются чаще, чем другие. Упорядочим их так: в качестве номера слова возьмём частоту n вхождения этого слова в тексты. Эту частоту назовём рангом, так что самое частое слово имеет ранг 1, второе по частоте слово имеет ранг 2 и т. д. Пусть P_n обозначает случайную частоту появления в тексте слова с рангом n. Тогда существует статистическое распределение, выражающее функциональную зависимость частоты P_n от ранга n. Бенуа Мандельброт объявил ранговое распределение законом языка. Этот закон представляется аналитической зависимостью [2], [12]:

P= k/(b+n),

где «гамма» приблизительно равна 1, постоянные величины k и b выражаются через частоту вхождения самого частого слова и длину текста.

Компьютерная обработка текстов показала, что закон Мандельброта не выражает математического ожидания, к которому, по вероятности, сходятся ранговые распределения слов длинных текстов. То есть не выполняется статистический закон больших чисел. Более того, на разных текстовых выборках слова не сохраняют вероятности вхождения. Таким образом, гипотеза Мандельброта о законе языка в форме рангового распределения не подтвердилась.

В 70–х гг. советский кибернетик Ю. Орлов предположил, что закон Мандельброта справедлив для завершённых текстов [2]. Тем самым поставлена задача исследования закономерностей целостного восприятия текстов различной природы: художественных, музыкальных, специализированных. Фактически, это подводит нас к проблеме моделирования смысловых отношений в знаковых системах, представляющих тексты.

В историческом плане работа в этом направлении только начинается. Впереди – открытия, которые помогут нам осознать закономерности функционирования интеллектуальных систем посредством изучения текстовых структур – основного интеллектуального продукта. Современное состояние исследований в этом направлении можно отражено в трудах научных конференций (см., например [2], [3], [12], а также указанную там библиографию).

Данное учебное пособие выполняет скромные функции семестрового курса математики, читаемого автором на гуманитарном факультете НГТУ. Целью курса является ознакомление студентов с идеями и методами математического формализма, т. е. математического языка. Автор считает, что математические тексты и структуры в определённом смысле являются образцами, представляющими простейшие интеллектуальные продукты. Насколько значительна роль математических стереотипов в исследовании общих текстовых структур, автору неизвестно. Очевидно лишь то, что рождение новых информационных технологий и автоматизация интеллектуального труда требует ревизии многих сложившихся формализаций в науке, и соответствующие исследования лежат в пересечении гуманитарных и точных наук.

Мы будем знакомиться с математикой как с искусственным языком и рассматривать ее в качестве интеллектуального ремесла. Поэтому главная наша задача состоит в том, чтобы понять назначение этого ремесла. Мы считаем, что смысл математического языка заключается в знаковой формализации канонических образов, которыми оперирует интеллект в различных информационных областях. Под знаковой формализацией образов мы понимаем направленное или волевое действие трех функций языка:

- присваивание мыслительному образу знака (действие опорной функции);

- оперирование образами как знаками (действие логической функции);

- реализация мысли в виде системы знаков (коммуникационная функция).

В указанном языковом смысле математику следует считать искусственной составляющей естественного интеллекта, развиваемой самим интеллектом для оптимизации своей деятельности.

Будем, например, считать одной из целей развития информационных технологий автоматизацию интеллектуального труда. Тогда мы с необходимостью признаем, что возможность компьютерного оперирования «образами» связано с преобразованием образов человеческих мыслей на язык отношений в определенных математических структурах. Поэтому для начала необходимо ответить на следующие вопросы:

- Как возникают математические структуры и что это такое?

- Как устроены такие структуры и как они функционируют?

Изучению этих вопросов мы посвящаем первую и вторую главы, названные нами, соответственно, «Математический формализм» и «Свойства аксиоматических систем».

Господь Бог создал натуральные числа; все остальное дело рук человеческих.

Леопольд Кронекер (1823–1891)

ГЛАВА I

МАТЕМАТИЧЕСКИЙ ФОРМАЛИЗМ

О понятии действительных чисел

Формализм натуральных чисел

  Ф.1. Эмпирические свойства, предопределяющие структуру натурального ряда. 1о. Любой объект может быть выбран …   Теперь займемся формализацией сформулированных свойств. Это означает, что требуется построить систему аксиом (правил),…

Вывод 1

Мы не будем обсуждать все свойства рациональных чисел, а ограничимся напоминанием свойств систематического представления рациональных чисел,… Наличие операций сложения и умножения позволяет построить представление целых… Такое представление дается записью вида: aN

Вывод 2

Аксиоматика рациональных чисел должна содержать правила, определяющие операции сложения, умножения, сравнения чисел и связь между этими операциями.

Замечание 1

(9) Объяснение того, что эта сумма представляет конечное число, основано на…

Аксиоматика рациональных чисел

Конструктивное определение рациональных чисел Q дано в схеме 2 предыдущего пункта. Приведем аксиоматическое определение. Оно содержит тот минимум правил, который обеспечил построение множества Q в предыдущем пункте.

 

Определение 1

Множество Q называется множеством рациональных чисел, а его элементы – рациональными числами, если выполняется следующий комплекс условий, называемый аксиоматикой рациональных чисел:

Аксиомы операции сложения

Для всякой упорядоченной пары х,у элементов из Q определен некоторый элемент х+у Î Q, называемый суммой х и у. При этом выполняются следующие условия:

1. (Существование нуля) Существует элемент 0 (нуль) такой, что для любого хÎQ

х+0=0+х=х.

2. Для любого элемента х Î Q существует элемент – х Î Q (противоположный х) такой, что

х + (–х) = (–х) + х = 0.

3. (Коммутативность) Для любых х,у Î Q

х + у = у + х.

4. (Ассоциативность) Для любых х,у,z Î Q

х + (у + z) = (х + у) + z.

Аксиомы операции умножения

Для всякой упорядоченной пары х, у элементов из Q определен некоторый элемент ху Î Q, называемый произведением х и у. При этом выполняются следующие условия:

5. (Существование единичного элемента) Существует элемент 1 Î Q такой, что для любого х Î Q

х ^.1 = 1^. х = х.

6. Для любого элемента х Î Q , (х0) существует обратный элемент х^–1 0 такой же, что

х^.х ^–1 = х^–1. х = 1.

7. (Ассоциативность) Для любых х, у,z Î Q

х ^. (у ^. z) = (х ^.у) ^. z.

8. (Коммутативность) Для любых х, у Î Q

х ^. у = у^. x.

Аксиома связи сложения и умножения

9. (Дистрибутивность) Для любых х, у, z Î Q

(х+у) ^. z = x ^. z+у ^. z.

Аксиомы порядка

10. (х у)L (у x) x=у. 11. (х у)L (у z) xz. 12. Для любых х, у Î Q либо х< у, либо у < x .

Аксиома связи сложения и порядка

13. Для любых x, y, z ÎQ, (x £ y) Þ x+z £ y+z.

Аксиома связи умножения и порядка

14. (0 £ x)Ç(0 £ y) Þ (0 £ x´y).

Аксиома непрерывности Архимеда

15. Для любых a > b > 0 существует m Î N и n Î Q такие, что m ³ 1, n < b и a= mb+n.

Следствие

1. Построить систематическую запись рациональных чисел при помощи конечного алфавита (цифровых символов). 2. Определить алгоритмы реализации операций ±, ´, :, £ в… 1.4. Задачи, приводящие к расширению множества рациональных чисел

Задача 1

Теорема Пифагора дает результат: искомая длина равна . Предположение о том, что = p/q – рациональное число опровергается известным доказательством… Заметим, что величина является решением уравнения x–2=0. Действительные… x+ ax+ … +ax + a = 0 (10)

Задача 2

Длина окружности L = 2pR, где R – радиус. В нашем случае L=3,1415… . Число p не является ни рациональным, ни алгебраическим, [4]. То, что число p не… Подчеркнем, что число p не является результатом применения алгебраических…

Вывод 3

Существуют числа, не являющиеся результатом конечного числа арифметических операций над целыми числами и не представимые в виде p/q ни для каких целых p, q.

Числа, не представимые в виде p/q ни для каких целых p, q, называются иррациональными.

Аксиоматизация множества действительных чисел

    Непрерывными операциями мы называем вычислительные алгоритмы, состоящие из арифметических и других простых операций,… Добавим к аксиомам, определяющим в п. З. множество рациональных чисел Q, еще…

Аксиома непрерывности Кантора.

То, что элемент Z, о котором говорится в этой аксиоме, является единственным, несложно доказать от противного.

Определение 2

Множество R называется множеством действительных чисел, а его элементы действительными числами, если они удовлетворяют всем тем же аксиомам 1–15, что и рациональные числа и, дополнительно, аксиоме непрерывности Кантора.

О представлении действительных чисел

Мы видели, что формирование аксиоматик множеств натуральных рациональных и действительных чисел связано с выполнением определенных операций над числами. Система записи или представления чисел связана и с другими задачами.

Задача 1

Построить символьную запись числа, в которой эффективно реализуются алгоритмы арифметических и алгебраических операций. Мы уже отмечали, что наиболее подходящей для этой цели является систематическая запись числа (десятичная, двоичная и др.)

Задача 2

Рассмотрим десятичные приближения. Пусть m = a, a, …,a– десятичное приближение с “k” знаками после запятой числа a = a, a, …,a,a,… . Тогда… |a–m/n| = a/10+a/10+…<9/10(1+1/10+…) = 9/10´ 1/(1–1/10) = 1/10~1/n.

Аксиоматическое обоснование евклидовой геометрии

Александрийский ученый Евклид, живший в третьем веке до нашей эры, впервые в истории предпринял попытку глобальной систематизации математических… Математические построения начинаются с 23 определений. Приведем некоторые из… · Точка есть то, что не имеет частей

Группа 1. Аксиомы соединения

1. Для любых двух различных точек существует прямая, инцидентная этим точкам. 2. Для любых двух различных точек существует не более одной прямой инцидентной… 3. Для каждой прямой существуют, по крайней мере, две точки, ей инцидентные. Существуют три точки, не инцидентные…

Теорема 1

Две различные точки определяют одну и только одну прямую им инцидентную.

Теорема 2

Три точки, не инцидентные одной прямой, определяют одну и только одну плоскость им инцидентную.

Теорема 3

Прямая и не инцидентная ей точка определяют одну и только одну плоскость, им инцидентную.

И так далее.

Группа 2. Аксиомы порядка

9. Если А, В, С – три точки, инцидентные прямой, и точка В лежит между точками А, С, то: а) точки А, В, С различны; б) точка В лежит между точками… 10. Для любых двух точек А, В, инцидентных прямой а, существует точка С прямой… 11. Для трех различных точек, инцидентных прямой, существуют не более одной из них, которая лежит между двумя…

Определение

Две точки на прямой А и В определяют отрезок.

Следствие

Согласно аксиомам 9–11 на этой прямой существуют точки, внешние и внутренние по отношению к отрезку АВ.

Определение

Совокупность трех точек А, В, С, не инцидентных одной прямой, и трех отрезков АВ, АС и ВС называется треугольником.

Аксиома Паша

12. Пусть задан треугольник АВС и в его плоскости прямая а, не проходящая через А, B, C. Если прямая а пересекает одну сторону АС треугольника, то она пересекает по крайней мере еще одну сторону.

Вот типичная теорема этой группы аксиом.

Теорема 4

Схема доказательства. (1) существует точка С, не принадлежащая прямой АВ (акс.3) (рис. 1); (2) существует точка D на прямой АС и точка C лежит между А и D;

Группа 3. Аксиомы конгруэнтности

13. Пусть даны отрезок АВ а также прямая а/ и точка . точка с заданной стороны относительно точки такая, что отрезок АВ конгруэнтен отрезку… 14. 15. Пусть АВ и ВС – отрезки на прямой , АВВС=В, тогда и лежит между и .

Теорема (о внешнем угле треугольника)

Внешний угол треугольника больше любого не смежного с ним угла треугольника.

Аксиомы 13–17 позволяют ввести операцию движения в геометрии.

Определение движения

Взаимно однозначное соответствие точек плоскости называется движением, если соответствующим парам точек , 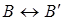соответствуют конгруэнтные отрезки

Замечание 1

В этой группе вместо аксиом 13–17 можно аксиоматически задать движение и некоторые его свойства. Тогда аксиомы 13–17 будут являться теоремами, которые доказываются на основании аксиом движения.

Вывод 1

Но в этой геометрии еще нет понятия параллельного переноса, не определено соответствие между действительными числами и точками прямой. Отсутствуют… Действительно, шаром В (O, OА) с центром в точке О и радиусом ОА назовем все… а) ОР1>ОР2>…>ОРк>…, что означает последовательность вложенных шаров…

Вывод 2

Используя лишь аксиомы I–III групп, мы не сможем установить существование предела у последовательности М_1, М_{2, …,} М_к, … , а в случае существования мы не сможем доказать его единственность.

Группа 4. Аксиомы непрерывности

    18. Аксиома Архимеда. Пусть даны два произвольных отрезка АВ и СD; существует такое натуральное n, что n·СD>АВ… 19. Аксиома Кантора. Пусть на прямой дана последовательность отрезков,… Аксиомы непрерывности 18–19 в геометрии и аксиомы непрерывности Архимеда и Кантора действительных чисел позволяют…

Замечание 2

Геометрия, построенная на 19 аксиомах групп 1–4, называется абсолютной геометрией. В этой геометрии ещё нет понятия параллельного переноса, поэтому ей принадлежат те и только те утверждения, которые не используют явно или неявно свойства параллельности.

Замечание 3

В абсолютной геометрии определено расстояние r(А,В) между любыми точками А и В, если определено понятие длины на прямой. r (А,В) = длине отрезка АВ. Расстояние обладает свойствами:

Вывод 3

Абсолютная геометрия содержит понятия числовых равенств элементов фигур (сторон, углов и т. д. ). В этой геометрии существуют понятия близости и непрерывности, основанные на понятии расстояния между точками фигур.

Группа 5. Аксиома параллельности

20. Через любую точку А, не инцидентную прямой “a” , можно провести в плоскости (определяемой этой точкой А и прямой “a”) не более одной прямой, не пересекающейся с “a”.

Замечание 4

Действительно, опустим перпендикуляр АВ на прямую “a”. Затем восстановим в точке А перпендикуляр “b” к прямой АВ (рис. 3.).     Если существует пересечение прямых “a” и “b” в… Итак, одна прямая, проходящая через точку и не пересекающая заданную прямую, существует. Но другую, отличную от этой,…

Два недостатка аксиоматики Д. Гильберта

Первым недостатком является «язык» аксиоматики. Дело в том, что часть формулируемых аксиом содержит понятия, обоснование которых проводится на… Второй «недостаток» состоит в том, что описание отношений между основными… Для аксиоматического построения многомерной евклидовой геометрии потребовалось переосмыслить процесс арифметизации…

Структура векторного пространства

Модель направленных отрезков

А. Построить систему свойств (аксиоматику), достаточную для описания модели направленных отрезков с операциями сложения и умножения на число. Решение сформулированной задачи состоит из двух частей: 1) в определении… Вначале определим операции и построим систему свойств (аксиом). Направленный отрезок есть отрезок AB заданной длины,…

Определение

В силу инвариантности направленных отрезков относительно параллельного переноса заключаем, что: 1) вектор – это класс направленных отрезков,… Множество всех векторов назовем векторным пространством, а построенную модель… Первая часть сформулированной задачи A нами решена. Для решения второй части этой задачи построим арифметическую…

Арифметическая модель векторного пространства

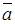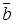Выражения вида a+b+…+g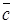называются линейными комбинациями векторов с действительными числами.

Теорема размерности

2. Пусть векторы лежат в плоскости П и 1 не параллелен 2. Тогда всякий вектор ÎП есть линейная комбинация векторов 1 и 2: = х 1 +у2. 3. Пусть векторы 1, 2 и 3 не лежат в одной плоскости. Тогда всякий вектор есть их линейная комбинация:

Вывод 1

↔(x,y,z), (1) определяемое разложением вектора в заданном базисе: . Чтобы объявить множество упорядоченных троек чисел арифметической или координатной моделью трехмерного векторного…

Вывод 2

Мы завершили решение сформулированной в начале параграфа задачи А. Вот это решение На множестве направленных отрезков система восьми свойств операции сложения… Попутно мы устанавливаем следующее свойство.

Вывод 3

, . (2) Это соответствие сохраняет результат линейных операций сложения векторов и… (3)

Абстрактное векторное пространство

Восемь свойств сложения и умножения, установленных в геометрической модели, позволяют построить арифметическую модель и называются аксиомами векторного пространства.

Рассмотрим примеры моделей, удовлетворяющих этим аксиомам.

Пример 1

Множество многочленов степени не выше

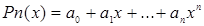
образует векторное пространство, в котором мономы – базисные элементы, а коэффициенты многочлена – координаты вектора в этом базисе.

Пример 2

Пусть 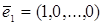, ,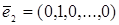…, 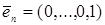– «–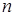местные наборы», 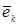имеет 1 на –м месте и нули на остальных местах, . Тогда объекты

образуют векторное пространство с базисными элементами . Обозначим это пространство .

Векторное пространство , позволяет определить размерность всякого векторного пространства 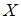при помощи следующей аксиомы.

9. Аксиома размерности. Существует изоморфизм .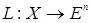

Определение абстрактного векторного пространства

Элементы множества могут быть произвольной природы. Например: · выборки измерений ; · цены наименований ;

Следствие

Множество многочленов степени не выше в примере 1 образуют –мерное пространство. Изоморфизм, устанавливающий размерность, задается в этом случае… , . Здесь – мономы, а – базисные орты в .

Аксиомы скалярного произведения векторов

Напомним, что в геометрической модели трехмерного скалярного произведения задается представлением . (4) В школьном курсе геометрии из этого представления выводятся три свойства:

Следствие

, . (6) Если в качестве базиса выбрать векторы , то, используя свойства 1–3, можно… ,

Следствие

. (8) Схему, по которой мы из определения скалярного произведения (4) получили… (9)

Вывод 4

В трехмерном векторном пространстве длина вектора (8) находится благодаря теореме Пифагора. В абстрактном векторном пространстве размерности больше трех аксиомами (5) задается скалярное произведение, а длина выражается через скалярное произведение по формуле (6). В арифметической модели 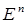скалярное произведение существует в виде (9), а длина вектора определяется согласно формуле (10).

Определение

Модель Вейля евклидовой геометрии

Арифметизация трехмерного евклидова пространства

Построим арифметическую, или координатную, модель евклидова пространства e3, используя координатную модель евклидова векторного пространства ,…

Свойства операции откладывания вектора

1. Для всякой фиксированной точки A₀Îe³ и произвольной точки BÎe³ отображение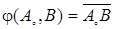

(1)

является взаимно однозначным отображением точек BÎe³ на множество векторов .

2.

(Аксиома треугольников). Для любых трех точек A,B,CÎe³ справедливо равенство

.

3. (Аксиома реализуемости операции откладывания). Существует хотя бы одна точка 0Îe³, для которой определена операция откладывания вектора 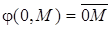для любой точки .

Точку в аксиоме 3 называют началом координат в евклидовом пространстве e³, а вектор – радиус–вектором точки в этом пространстве. Координатами 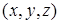точки MÎe³ называют координаты радиус–вектора (рис. 7), где 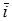, , 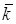– направленные отрезки в e³, соответствующие базисным векторам 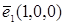, , векторного пространства при отображении (1) с . Таким образом, по построению операции откладывания вектора в e³ приходим к векторному равенству

. (2)

Это равенство, с учетом фиксированной точки 0Îe³, представляет взаимно однозначное соответствие между точками MÎe³ и арифметическими упорядоченными тройками чисел 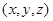и является определяющим равенством для координат точек евклидова пространства.

Для вычисления длин отрезков и углов между ними воспользуемся свойствами скалярного произведения (4), (6), (7), (8) из §3, а также свойством 1 операции откладывания отрезка.

Пусть требуется найти длину отрезка 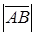, если заданы координаты его концов 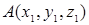и 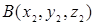. Учитывая, что , из формулы (8) § 3 находим длину

(3)

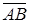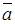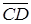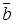Пусть = (u₁,v₁,w₁) и = (u₂,v₂,w₂) – направленные отрезки в e³ и пусть их координаты (u₁,v₁,w₁) (u₁,v₁,w₁) в Е³. Тогда, используя формулы (4), (7) и (8) из §3, получаем формулу для косинуса угла между 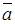и

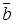
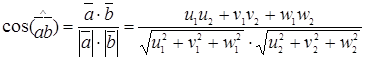(4)

Определение

Арифметической, или координатной, моделью евклидова пространства e³ называется множество упорядоченных троек чисел, определяемых соответствием (2) вместе с формулами длины отрезка (З) и углов между направленными отрезками (4), выраженными через скалярное произведение. Арифметическую модель трехмерного евклидова пространства будем обозначать R³.

Вывод 1

· геометрическую модель трехмерного векторного пространства (модель направленных отрезков e3); · изоморфную модель координатного векторного пространства Е3; · операцию откладывания вектора (1);

Вывод 2

Решение геометрических задач в модели R³ сводится к решению систем уравнений.

Многомерное арифметическое евклидово пространство

I. Группа аксиом векторного пространства. Эта группа включает восемь аксиом векторного пространства, сформулированных в… II. Аксиомы скалярного произведения.

Вывод 3

Замечание

Аксиоматическое обоснование евклидовой геометрии по Вейлю – наиболее распространенная схема построения арифметической модели Rⁿ, применяемой в задачах линейного программирования, исследования операций и т.д.

Модель А. Пуанкаре плоскости Лобачевского

Основные понятия модели А. Пуанкаре плоскости Лобачевского

Аксиомы 1–3 I группы аксиом Д. Гильберта вместе с остальными аксиомами II–V групп образуют систему 15 аксиом евклидовой плоскости (см. п.2.2 §2). Заменим аксиому параллельности V этой группы на следующую аксиому.

V’. Аксиома параллельности Лобачевского

Через любую точку A, не инцидентную прямой a, можно провести в плоскости, определяемой точкой A и прямой a, по крайней мере, две различные прямые, не пересекающиеся с прямой a.

Определение плоскости Лобачевского

Эта модель неевклидовой геометрии была опубликована Н. И. Лобачевским в его известной работе «О началах геометрии» в журнале «Казанский вестник» в… То, что существует хотя бы одна прямая, проходящая через точку A вне прямой a… Рассмотри кратко эту модель, опуская доказательства, которые можно найти, например, в [7].

Следствие 1

В плоскости L₂ через точку A вне прямой a проходит бесконечное множество прямых, не имеющих общих точек с a (расходящихся с a). При этом существует в точности две параллельные g₁ и g₂, имеющие общие точки с a на абсолюте l

A_¥ = g₁ Ç aÎ l, A_¥ = g₂ Ç aÎ l,

Вывод

В модели L₂ выполняются 15 аксиом планиметрии Лобачевского.

Основные факты в планиметрии Лобачевского

Ограничимся иллюстрацией ряда свойств взаимного расположения прямых на плоскости L2. Строгое доказательство этих фактов можно найти, например, в… 1. Сумма углов многоугольника в плоскости L2     Рассмотрим треугольник (рис. 11, а) с вершинами, лежащими на абсолюте. Так как, по…

Следствие 2

В плоскости Лобачевского L₂ сумма углов треугольника не постоянна и может принимать любое значение больше нуля и меньше p.

2. Взаимное расположение прямых в плоскости L₂

Всякие две прямые в плоскости L₂ либо пересекаются, либо параллельны, либо являются расходящимися, т.е. не параллельны и не пересекаются, рис. 3.

Перпендикуляр к стороне угла

Четвертый признак конгруэнтности треугольников

В абсолютной геометрии без привлечения аксиомы параллельности доказываются три признака конгруэнтности треугольников. В планиметрии Лобачевского справедлив еще один, четвертый признак. Если три угла одного треугольника конгруэнтны соответствующим трем углам второго треугольника, то эти треугольники конгруэнтны [7].

Вывод 2

Рассмотренные выше неевклидовы отношения 1–4 между прямыми на плоскости Лобачевского являются логическим следствием 15 аксиом планиметрии Лобачевского и реализуются в модели Пуанкаре L₂.

О роли открытия неевклидовой геометрии

В современной науке понятие реализации или модели некоторой системы аксиом используется для проверки основных требований, предъявляемых к…

Вывод 3

Формирование математических текстов на основе дедуктивного метода, т.е. построение теории на базе системы аксиом, должно удовлетворять некоторым… Лучший метод для предвидения будущего развития математических наук заключается… Анри Пуанкаре

ГЛАВА II

СВОЙСТВА АКСИОМАТИЧЕСКИХ СИСТЕМ

Математические структуры и аксиоматические теории

Понятие отношений между объектами

(x,y) ÎP Û {выполняется Ð (x,y)} (1) Множество упорядоченных пар (x,y) "xÎA и "yÎB называется…

Следствие 1

Всякое бинарное или двухместное отношение Ð(x,y) между элементами x, y двух множеств A'x и B'y представляется некоторым подмножеством P(x,y)ÌA´B по закону (1). Обратно, всякое подмножество PÌA´B по этому же закону (1) представляет некоторое отношение Ð(x,y).

Пример 1

Пусть A=B=R – множество действительных чисел. Тогда R´R есть декартово произведение евклидовых прямых. Это произведение представляет собой арифметическую модель евклидовой плоскости. (Другими словами, множество числовых упорядоченных пар (x,y), "xÎR, "yÎR представляет все точки евклидовой плоскости.)

Определение

1. Рефлексивности x~x; 2. Симметричности: если x~y, то y~x; 3. Транзитивности: если, x~y, y~z, то x~z.

Следствие 2

Аналогично двухместному определяются n–местные отношения между элементами xÎA,…,xÎAнекоторых множеств A, …, A. Декартово произведение A´A´…´Aесть множество упорядоченных…  

Понятие математической структуры

Пеано для натуральных чисел. Аксиоматика действительных чисел. Аксиоматика векторных пространств.

Определение

Таким образом определенную математическую структуру будем обозначать = {T, Ð, M}. Для краткости эту структуру, соответствующую системе аксиом T,…

Примеры

Указанные в начале пункта аксиоматики задают, соответственно, структуры: натуральных чисел, действительных чисел, векторных пространств, структуру геометрического евклидова пространства и структуру арифметического евклидова пространства.

Определение

Система всех утверждений, доказываемых логическим путем в структуре , называется аксиоматической теорией этой структуры. Аксиоматическую теорию структуры будем обозначать символом .

Пример

Теорема о внешнем угле треугольника: внешний угол треугольника больше любого не смежного с ним угла треугольника является элементом теории структуры абсолютной планиметрии (геометрии плоскости, построенной в системе 14 аксиом планиметрии без аксиом параллельности).

Модель или реализация системы аксиом

Модель или реализация системы аксиом T называется также моделью или реализацией как аксиоматической теории , так и структуры . Эту реализацию будем… Приведем примеры реализаций. Модель линейного порядка Торальфа Сколема (см. п. 1.1 §1) является моделью, или реализацией, аксиоматики Пеано или…

Замечание 1

6.4. Формальная и содержательная аксиоматики. Теории и структуры Пусть R(T) – реализация некоторой системы аксиом Т. Рассмотрим подробнее, что… 1) некоторые объекты Ri (Mi), являющиеся реализациями базовых множеств M1…, Mm так, что существует взаимно однозначное…

Рассмотрим пример

Пусть R² – арифметическая модель евклидовой плоскости. Тогда базовое множество М₁ – это все точки M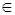R², реализующиеся как упорядоченные числовые пары (x,y). Множество H₂ – это множество всех прямых lR², реализующихся уравнениями вида ax+by+c = 0. Отношение Ð₁(M,l)(M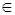l) – точка М принадлежит прямой l, реализуется свойством P₁: пара (x,y) удовлетворяет уравнению ax+by+c = 0, и т.д.

Вывод 1

Вывод 2

Всякое утверждение А теории получается логическим заключением (выводом) и в реализации R(T) находится соответствующее отношение между объектами, отражающее утверждение А.

Определение

Если существует реализация R(T) этой системы, то система Т, теория и структурой называются содержательными. Классическим примером формальной теории является геометрия Лобачевского. Эта… Чтобы использовать реализации R(T) для исследования аксиоматических систем Т, введем понятие изоморфизма реализаций…

Изоморфизм

  (2)  

Пример 1

Пусть система аксиом Т состоит из 14 аксиом аксиоматики Гильберта, определяющих абсолютную геометрию плоскости (геометрию без аксиомы параллельности). Мы имеем две реализации этой планиметрии:

(1) арифметическая модель R² (евклидовой плоскости);

(2) модель Пуанкаре L₂ (плоскости Лобачевского). Можно установить взаимно однозначное соответствие между точками М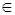R² и точками N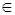L₂, а также между прямыми l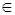R² и прямыми a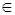L₂. В то же время не всем отношениям между точками и прямыми в L₂ можно найти соответствующие отношения в R². Например, отношение Ð(a₁, a₂) прямые a₁ и a₂ не параллельны и не пересекаютсяможет выполняться в L₂ и не имеет аналога в R². (Другие неевклидовы отношения между точками и прямыми на плоскости L₂ см. в п. 5.2 §5).

Пример 2

Пусть e² – геометрическая модель направленных отрезков (выполненная, например, карандашом на бумаге или реализованная на мониторе компьютера). Пусть Е²– арифметическая модель векторного пространства. Операция откладывания вектора, указанная в модели Вейтеля (п.4.1 §4), устанавливает взаимно однозначное отображение 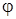: 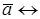(x,y) модели e²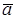на модель Е²(x,y). При этом, отображение 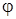сохраняет все определенные в векторной структуре отношения между соответствующими векторам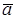и и 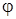(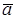)=(x,y).

Определение изоморфизма

1) существует взаимно–однозначное соответствие (2) между реализациями Ri(Mi) и R'i(Mi) базовых множеств Mi, i=1,2,…, m; 2) отображение (2) устанавливает взаимно однозначное соответствие между всеми… Само отображение (2) при этом называется как изоморфизмом моделей или реализацией R(T) и R'(T), так и изоморфизмом…

Вывод 3

Вывод 4

Разница между абстрактной (формальной) системой аксиом с некоторой реализацией и содержательной системой аксиом состоит только в способе построения структуры. Действительно, можно вначале построить абстрактную систему аксиом, а затем указать ее модель. Можно наоборот, вначале выбрать те свойства модели, которые определяют ее с точностью до изоморфизма, а затем эти свойства принять за аксиомы. Оба способа определяют две изоморфные структуры.

Вывод 5

Требования , предъявляемые к системам аксиом

Непротиворечивость системы аксиом

Теория , содержащая вместе с некоторым утверждением АÎи отрицание этого утверждения ùАÎназывается не классической теорией. С… Теоретическая проверка совместности системы аксиом, основанная на… Мы уже говорили, что с точки зрения здравого смысла противоречивая система аксиом не должна допускать никакой…

Вывод 1

В качестве примера обратимся к трехмерной евклидовой геометрии. Так как одной из ее реализаций является арифметическая модель R3 (координатная… Если в качестве реализации евклидовой геометрии рассматривать окружающий нас… В качестве второго примера рассмотрим планиметрию Лобачевского. Она имеет реализацию Пуанкаре L2, см. §5. В свою…

Независимость аксиоматической системы

Для иллюстрации этого свойства обратимся снова к геометрической теории, основанной на аксиоматике Гильберта. Ясно, что непосредственная проверка… Сформулируем назревший вопрос. Существует ли эффективное достаточное условие… Пусть Т – непротиворечивая система аксиом. Утверждение (аксиома) А не зависит от системы Т, если вместе с некоторой…

Независимость аксиомы параллельности

Замечание 1

Доказательство независимости всех аксиом евклидовой геометрии можно найти, например, в [7], [8].

Дедуктивная полнота и категоричность системы аксиом

И=ДUОUН. (1)

Определение (дедуктивной полноты)

Другими словами, в теории всех высказываний такой системы Т недоказуемые и неопровержимые (неопределенные) утверждения отсутствуют и разложение (1)… И=ДUО. (2) Например, система аксиом Т абсолютной геометрии, состоящая из аксиом Д. Гильберта с исключенной аксиомой П –…

Определение (категоричности)

Рассмотренная выше система аксиом абсолютной геометрии представляет пример некатегоричной системы аксиом, так как существуют две неизоморфные… Приведем без доказательства следующий критерий дедуктивной полноты. Если… Обратное утверждение не справедливо. Существуют примеры дедуктивно полных систем аксиом, у которых имеются…

Анализ текстовых парадоксов

Языковые свойства имен объектов

Денотат имени – это предметное значение имени, т.е. сам именуемый объект. Концепт имени – это смысловое значение имени, т.е. то объективное содержание,… Константы – это сами имена индивидуальных предметов, но не имена свойств и отношений.

Пример 1

“Число 2” – это имя имеет определенный денотат и концепт.

Пример 2

Имена: “Отношение эквивалентности”, “подобие”, “параллельность” имеют определенный концепт, как некоторые отношения. В то же время денотаты этих имен не определены.

Пример 3

Имя ““ – символ, представляющий определенный денотат – число 2. Однако, его концепт неопределен: – операция или – величина?

Проблема выразимости

В конце концов, смысл предложения как знаковой цепочки становится неопределенным. Мера определенности, по-видимому, является мерой символьной длины… Математики всегда сознавали несовершенство естественного языка. Громоздкие… Однако символьный язык не смог полностью заменить естественный язык, так как язык изложения по необходимости всегда…

Понятие искусственного языка

1. Алфавит (конечный список исходных символов). 2. Правила построения термов (имен и именных форм). 3. Правила построения формул (высказываний и высказывательных форм).

Понятие парадокса

Парадоксами будем называть текстовое утверждение, логическое следствие которого приводит к противоречиям. Мы выделим два типа соответствия между языками моделей. Первый тип. Согласно выводу 3, §6, изоморфизм мыслимой модели на некоторою внешнюю модель дает возможность…

Парадокс пустого множества

Рассмотрим утверждение “Т” как аксиому и рассмотрим существование реализации R(T) мыслимой модели с аксиомой Т. Реализация есть пустое множество. В… Утверждение такого типа, когда мыслимые модели не имеют реальных моделей,…

Парадокс достижимости в натуральном ряде

Вопрос: всякий ли элемент xÎN достижим? Для ответа воспользуемся аксиомой 5 “Математической индукции” аксиоматики Пеано (см. п.1.1. §1). Пусть… С другой стороны, как мы знаем (п.1.1. § 1), линейная цепь Т = 1, 2, ... , n, ... ; ..., а–2, а –1, а0, а1, а2, ... ; ... ,

Вывод

В теории аксиом Пеано свойство достижимости не доказуемо и не опровержимо, подобно тому, как в абсолютной планиметрии не доказуема и не опровержима аксиома параллельности.

8.8. “Одно и то же, но по–разному”

– именно так характеризуется аксиоматическая теория, имеющая две неизоморфные модели. Напомним, п.7.4 §7, что такие аксиоматики, аксиоматические теории и структуры называются некатегоричными, и рассмотрим примеры.

Вначале напомним, что система 15 аксиом (часть аксиом Гильберта) определяет геометрию e² плоскости Евклида. Если заменить аксиому параллельности Евклида на аксиому параллельности Лобачевского, то получим систему 15 аксиом планиметрии Лобачевского с моделью Пуанкаре L_2. Напомним также, что обе эти геометрии образуют дедуктивно полные и категоричные аксиоматические теории. Теперь сформулируем пример.

Пример 1

Из 15 аксиом планиметрий Е² и L₂ удалим аксиомы параллельности. Оставшиеся 14 аксиом составляют Теорию абсолютной планиметрии. Эта теория не категорична, так как L₂ не изоморфна R². Эта теория дедуктивно не полна, т.к. аксиома параллельности не выводима из остальных аксиом.

Таким образом, одна и та же система аксиом абсолютной планиметрии в разных моделях имеет различные “визуальные” эффекты. Например, в плоскости L_2, (см. §5) мы “видим” два равных треугольника по трем равным углам, а также две прямые, которые не параллельны и не пересекаются. Этого “увидеть” в плоскости R² мы не можем.

Пример 2

Рассмотрим теорию, определяемую следующими 7 аксиомами:

1. Аксиома рефлексивности: "х(х£х).

2. Аксиомы антисимметричности: "х,у(х£у Ù у£х Þ х=у).

3. Аксиома транзитивности: "х,у,z(х£у Ù у£z Þ х£у).

4. Аксиома линейности: "х,у(х£у Ú у£х).

5. Аксиома плотности: "х,у$z(х¹у Þ х<z<у Ú y<z<x)

6. Аксиома отсутствия наименьшего элемента: "х$z (z<y).

7. Аксиома отсутствия наибольшего элемента: "х$z (z>y).

 

Эта система аксиом дедуктивно полна (см., например, [11]) но не категорична, так как имеет две неизоморфные модели: Q – множество рациональных чисел и R – множество действительных чисел.

Заключение

Мы закончили экскурс в математику кратким анализом текстовых парадоксов. Любой парадокс является интеллектуальным продуктом. Как противоречие он обнаруживается при построении изоморфизмов моделей и выражается в виде текста символьного и описательного языков. Поэтому все парадоксы можно в определенном смысле считать текстовыми.

Язык изложения нашего чрезвычайно краткого курса по алгоритмичности не выходит за рамки школьной программы, но по культуре мышления требует дополнительных интеллектуальных усилий.

По возможности мы демонстрировали язык геометрического формализма и геометрических моделей. Этот язык максимально приближен к наглядности. Наглядность – это визуальное представление информации. Строгость такого представления не “ниже”, чем в абстрактной символьной модели. Строгость языка рассмотренных геометрических моделей определяется свойствами непротиворечивости, независимости, категоричности и дедуктивной полноты аксиоматик Гильберта, Вейля и Лобачевского.

Таким образом, уровень строгости языка определяется свойствами выразимости и не зависит от степени “наглядности” или абстрактности.

Примеры п.8.8 §8 показывают, что “дефекты” выразимости присущи как визуальным, так и абстрактным аксиоматическим системам.

Какой мы сделаем вывод в конце нашего краткого курса?

Напомним три основные функции естественного языка: 1) отслеживание мысли, 2) формирование умозаключений и 3) средство коммуникаций.

Первые две функции в естественном языке используются для построения мыслимых моделей и являются инструментом процесса мышления (интеллекта). Третья функция использует знаковые системы для связи субъекта с внешним миром и является инструментом для реализации продукта мышления. Поскольку интеллект есть процесс или продукт мыслительной деятельности, то язык является единственным инструментом интеллекта.

Математический язык – это искусственный язык, который позволяет оптимально кодировать, хранить и передавать информацию. Например, 20 аксиом геометрии вместе с заданием точек, прямых, плоскостей и отношениями (принадлежности, порядка, конгруэнтности, параллельности и непрерывности) образуют геометрический язык и позволяют «хранить» в геометрической структуре около 20.000 утверждений, которые составляют предмет геометрической теории и могут быть выведены в рамках этой теории.

Язык геометрии строился несколько тысячелетий. Можно предположить, что основные геометрические структуры, изученные нами, являются каноническими моделями, по образу и подобию которых строятся многие естественно–научные модели и теории. Мы видели, что визуальность евклидовой геометрии не делает ее «менее строгой», чем чисто логические построения. Действительно, геометрические аксиоматики обладают свойствами совместности, независимости (при условии, что этими свойствами обладают действительные числа) и дедуктивной полнотой, которая следует из категоричности. Поэтому можно считать, что качество модели, иллюстрирующих какие–либо явления, также определяются наличием свойств совместности, независимости и дедуктивной полноты системы аксиом, определяющих эти модели.

Рассмотрим пример. Компьютерную игру назовем «Абсолютная геометрия». Ее правила – законы структуры планиметрии без аксиомы параллельности. Результат игры состоит в правильном ответе “да” или “нет” на любое утверждение, сформулированное на языке геометрических отношений, задаваемых 14 аксиомами планиметрии без аксиомы параллельности (см. замечание 2, п. 2 §2).

- Вопрос: Равны или нет два треугольника по трем равным сторонам?

- Ответ : Да.

Действительно, этот признак равенства треугольников не зависит от аксиомы параллельности.

- Вопрос: Равны два треугольника по трем равным углам?

- Ответ: Ни да, ни нет!

Действительно, в арифметической модели евклидовой плоскости R² ответ: “нет”; в модели Пуанкаре плоскости Лобачевского ответ: “да!” Такая неопределенность ответа связана с дедуктивной неполнотой абсолютной планиметрии. Следовательно, абсолютная планиметрия “некачественная” модель плоскости, так как некоторые вопросы не имеют определенного ответа.

Геометрическая визуальность – понятие относительное. Действительно, стоило нам поменять аксиому параллельности Евклида на аксиому Лобачевского, и мы получили абстрактную планиметрию Лобачевского. Визуальность практически исчезает, но высшая “степень качества” геометрической модели остается.

Мы выяснили, что объектами математического языка являются только математические структуры. Основу Теории математических структур составляют те же три функции, которые выделяют в естественном языке. Поэтому математике отводится роль имитации мыслительных процессов в формализованной знаковой системе. Можно считать, что математика создает искусственный интеллект, который развивается параллельно естественному интеллекту и в определенном смысле оптимизирует работу последнего.

Формы познания человеком окружающей действительности имеет единую сущность, которая выражается в законах самоорганизации сложных систем. В знаковых системах, используемых человеком для создания мыслительного образа, его преобразования и реализации в виде модели, концентрируются законы, по которым организуется любое мыслительное познание мира. Применяя математику как языковой инструмент исследования, в любом случае, мы накапливаем интеллектуальный опыт и концентрируем его в знаковой системе по закону математической структуры. Отношение интеллектуального опыта к реальности определяется различными реализациями, возникающими в человеческой практики.

Обозначения.

Þ – знак логического следствия “отсюда следует, что”; Û – знак эквивалентности утверждений “тогда и только тогда, когда”; Ç – знак пересечения множеств;

ЛИТЕРАТУРА

 

 

1. Клайн М. Математика. Утрата определенности. – М.: Мир, 1988.

2. Орлов Ю.К. Невидимая гармония. Число и мысль. – М.: 1980. Вып.3.-c. 73/

3. Квантитативная лингвистика и семантика. Сборник научных трудов. вып.1.– Новосибирск, изд–во НГПУ,1999.

4. Бухштаб А.А. Теория чисел. – М.:1960.

5. Гильберт Д., Кон–Фоссен. Наглядная геометрия. – М.: Наука, 1981.

6. Хинчин А.Я. Цепные дроби. – М.: ФМ, 1961.

7. Ефимов Н.В. Высшая геометрия. – М.: Наука, 1978.

8. Пуанкаре А. О науке. – М.: Наука, 1983.

9. Александров А.Д. Основание геометрии. – М.: Наука, 1987.

10. Биркгофф Г. Математика и психология. – М.: Советское радио, 1977.

11. Колмогоров А.Н., Драгалин А.Г. Введение в математическую логику. – М.: Изд-во МГУ, 1982.

12. Мандельброт. Б. Теория информации и психолингвистика: теория частот слов. //Математические методы в социальных науках. – М.: Прогресс, 1973,-с. 316–337.