Решение линейных уравнений в MathCad

Решение уравнений с одним неизвестным

Рассмотрим одно алгебраическое уравнение с одним неизвестным х.

f(x)=0, (1)

например, sin(x)=0.

Для решения таких уравнений Mathcad имеет встроенную функцию root, которая, в зависимости от типа задачи, может включать либо два, либо четыре аргумента и, соответственно, работает несколько по-разному:

root(f(х),х);

root(f(х),х,а,b);

f (х) – скалярная функция, определяющая уравнение (1); х – скалярная переменная, относительно которой решается уравнение; а,b – границы интервала, внутри которого происходит поиск корня.

Первый тип функции root требует дополнительного задания начального значения переменной х. Для этого нужно просто предварительно присвоить х некоторое число. Поиск корня будет производиться вблизи этого числа. Таким образом, присвоение начального значения требует априорной информации о примерной локализации корня.

Пример решения простого уравнения sin(x)=0, корни которого известны заранее.

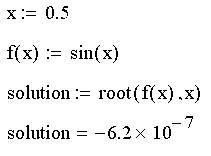
Рис. 1. Графическое решение уравнения sin(x)=0

График функции f (x)=sin(x) и положение найденного корня показаны на рис. 1. Обратите внимание, что, хотя уравнение имеет бесконечное количество корней x_n=np (n=0,±1,±2,...), Mathcad находит (с заданной точностью) только один из них, х₀, лежащий наиболее близко к х=0.5. Если задать другое начальное значение, например х=3, то решением будет другой корень уравнения х₁=p и т. д. Таким образом, для поиска корня средствами Mathcad требуется его предварительная локализация. Это связано с особенностями выбранного численного метода, который называется методом секущих и состоит в следующем (рис. 2):

· Начальное приближение принимается за нулевое приближение к корню: х₀=х.

· Выбирается шаг h=TOLх и определяется первое приближение к корню x₁=x₀+h. Если х=0, то принимается h=TOL.

· Через эти две точки проводится секущая – прямая линия, которая пересекает ось х в некоторой точке х₂. Эта точка принимается за второе приближение.

· Новая секущая проводится через первую и вторую точки, тем самым определяя третье приближение, и т. д.

· Если на каком-либо шаге оказывается, что уравнение выполнено, т. е. |If (x) |<TOL, то итерационный процесс прерывается, и х выдается в качестве решения.

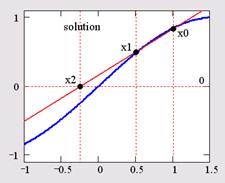
Рис. 2. Иллюстрация метода секущих

Если уравнение неразрешимо, то при попытке найти его корень будет выдано сообщение об ошибке. Кроме того, к ошибке или выдаче неправильного корня может привести и попытка применить метод секущих в области локального максимума или минимума f (х). В этом случае секущая может иметь направление, близкое к горизонтальному, выводя точку следующего приближения далеко от предполагаемого положения корня. Для решения таких уравнений лучше применять другую встроенную функцию Minerr. Аналогичные проблемы могут возникнуть, если начальное приближение выбрано слишком далеко от настоящего решения или f (х) имеет особенности типа бесконечности.

Иногда удобнее задавать не начальное приближение к корню, а интервал [а,b], внутри которого корень заведомо находится. В этом случае следует использовать функцию root с четырьмя аргументами, а присваивать начальное значение х не нужно. Поиск корня будет осуществлен в промежутке между а и b альтернативным численным методом (Риддера или Брента).

Поиск корня алгебраического уравнения в заданном интервале

Обратите внимание, что явный вид функции f (х) может быть определен непосредственно в теле функции root.

Когда root имеет четыре аргумента, следует помнить о двух ее особенностях:

– внутри интервала [а,b] не должно находиться более одного корня, иначе будет найден один из них, заранее неизвестно, какой именно;

– значения f (а) и f (b) должны иметь разный знак, иначе будет выдано сообщение об ошибке.

Отметим, что f (х) может быть функцией не только х, а любого количества аргументов. Именно поэтому в самой функции root необходимо определить, относительно какого из аргументов следует решить уравнение. Эта возможность проиллюстрирована на примере функции двух переменных f (х,у)=х²–y²+3. В нем сначала решается уравнение f(x,0)=0 относительно переменной х, а потом - другое уравнение f (1,у) =0 относительно переменной у.

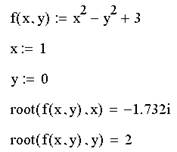
Корни полинома

Если функция f (х) является полиномом, то все его корни можно определить, используя встроенную функцию polyroots(v), где v - вектор, составленный из коэффициентов полинома.

Поскольку полином N-й степени имеет ровно N корней (некоторые из них могут быть кратными), вектор v должен состоять из N+I элемента. Результатом действия функции polyroots является вектор, составленный из N корней рассматриваемого полинома. При этом нет надобности вводить какое-либо начальное приближение, как для функции root. Пример поиска корней полинома четвертой степени.

Коэффициенты рассматриваемого в примере полинома

f (х) = (х-3)×(х-1)³=х⁴–6х³+12х²–10х+3

записаны в виде вектора в первой строке. Первым в векторе должен идти свободный член полинома, вторым – коэффициент при х₁ и т. д. Соответственно, последним n+1 элементом вектора должен быть коэффициент при старшей степени х_n.

Иногда исходный полином имеется не в развернутом виде, а, например, как произведение нескольких полиномов. В этом случае определить все его коэффициенты можно, выделив его и выбрав в меню Symbolics (Символика) пункт Expand (Разложить). В результате символьный процессор Mathcad сам преобразует полином в нужную форму, пользователю надо будет только корректно ввести ее в аргументы функции polyroots.

Во второй строке показано действие функции polyroots. Обратите внимание, что численный метод вместо двух из трех действительных единичных корней (иными словами, кратного корня 1) выдает два мнимых числа. Однако малая мнимая часть этих корней находится в пределах погрешности, определяемой константой TOL, и не должна вводить пользователей в заблуждение. Просто нужно помнить, что корни полинома могут быть комплексными, и ошибка вычислений может сказываться как на действительной, так и на комплексной части искомого корня.

Для функции polyroots можно выбрать один из двух численных методов - метод полиномов Лаггера (он установлен по умолчанию) или метод парной матрицы.

Решение системы уравнений

Рассмотрим решение системы N нелинейных уравнений с M неизвестными

f₁(x₁, ... ,х_м) = 0,

… ()

f_n(x₁, ... ,х_м) = 0,

Здесь f₁(x₁, ... ,х_м) , ..., f_n(x₁, ... ,х_м) - некоторые скалярные функции от скалярных переменных х₁,х₂,...,х_м и, возможно, от еще каких-либо переменных. Уравнений может быть как больше, так и меньше числа переменных. Заметим, что систему () можно формально переписать в виде

f(x)=0, ()

где х – вектор, составленный из переменных x₁,х₂,...,х_м, a f (х) - соответствующая векторная функция.

Для решения систем имеется специальный вычислительный блок, состоящий из трех частей, идущих последовательно друг за другом:

Given – ключевое слово;

система, записанная логическими операторами в виде равенств и, возможно, неравенств;

Find(x1,...,хм) – встроенная функция для решения системы относительно переменных х1,...,хм.

Вставлять логические операторы следует, пользуясь панелью инструментов Boolean (Булевы операторы). Блок Given/Find использует для поиска решения итерационные методы, поэтому, как и для функции root, требуется задать начальные значения для всех х1, ... ,xм. Сделать это необходимо до ключевого слова Given. Значение функции Find есть вектор, составленный из решения по каждой переменной. Таким образом, число элементов вектора равно число аргументов Find.

Ниже приведен пример решения системы двух уравнений.

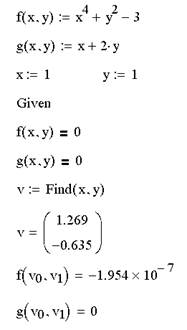
В первых двух строках вводятся функции, которые определяют систему уравнений. Затем переменным х и у, относительно которых она будет решаться, присваиваются начальные значения. После этого следует ключевое слово Given и два логических оператора, выражающих рассматриваемую систему уравнений. Завершает вычислительный блок функция Find, значение которой присваивается вектору v. Следующая строка показывает содержание вектора v, т. е. решение системы. Первый элемент вектора есть первый аргумент функции Find, второй элемент – ее второй аргумент. В последних двух строках осуществлена проверка правильности решения уравнений.

Отметим, что уравнения можно определить непосредственно внутри вычислительного блока. Таким образом, можно не определять заранее функции f (x,y) и g(х,у), как это сделано в первых двух строках, а сразу написать:

Given

х⁴ + у² =3

х+ 2у = 0

Такая форма представляет уравнения в более привычной и наглядной форме, особенно подходящей для документирования работы.

Графическая интерпретация рассмотренной системы представлена на рис. 3. Каждое из уравнений показано на плоскости XY графиком. Первое – сплошной кривой, второе – пунктиром. Поскольку второе уравнение линейное, то оно определяет на плоскости XY прямую. Две точки пересечения кривых соответствуют одновременному выполнению обоих уравнений, т. е. искомым действительным корням системы. Как нетрудно убедиться, в примере найдено только одно из двух решений – находящееся в правой нижней части графика. Чтобы отыскать и второе решение, следует повторить вычисления, изменив начальные значения так, чтобы они лежали ближе к другой точке пересечения графиков, например x=-1, y=-1.

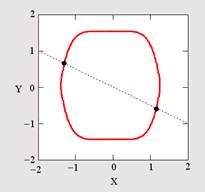
Рис. 3. Графическое решение системы двух уравнений

Число уравнений и неизвестных может не совпадать, а в вычислительный блок можно добавить дополнительные условия в виде неравенств. Например, введение ограничения на поиск только отрицательных значений х в рассмотренный выше примере приведет к нахождению другого решения, как это показано ниже.

Обратите внимание, что, несмотря на те же начальные значения, что и в примере 1, мы получили здесь другой корень. Это произошло именно благодаря введению дополнительного неравенства.

Если предпринять попытку решить несовместную систему, Mathcad выдаст сообщение об ошибке, гласящее, что ни одного решения не найдено, и предложение попробовать поменять начальные значения или значение погрешности.

Особенную осторожность следует соблюдать при решении систем с числом неизвестных большим, чем число уравнений. Например, можно удалить одно из двух уравнений из рассмотренного нами примера, попытавшись решить единственное уравнение g(х,у)=0 с двумя неизвестными х и у. В такой постановке задача имеет бесконечное множество корней: для любого х и, соответственно, у=-х/2 условие, определяющее единственное уравнение, выполнено. Однако, даже если корней бесконечно много, численный метод будет производить расчеты только до тех пор, пока логические выражения в вычислительном блоке не будут выполнены (в пределах погрешности). После этого итерации будут остановлены и выдано решение. В результате будет найдена всего одна пара значений (х,у), обнаруженная первой.

Приближенное решение уравнений

Иногда приходится заменять задачу определения корней системы уравнений задачей поиска экстремума функции многих переменных. Например, когда невозможно найти решение с помощью функции Find, можно попытаться потребовать вместо точного выполнения уравнений условий минимизировать их невязку. Для этого следует в вычислительном блоке вместо функции Find использовать функцию Minerr, имеющую тот же самый набор параметров. Она также должна находиться в пределах вычислительного блока:

x1:=C1 ... хм: =Cм – начальные значения для неизвестных.

Given – ключевое слово.

Система алгебраических уравнений и неравенств, записанная логическими операторами.

Minerr (x1,... ,хм) – приближенное решение системы относительно переменных х1;... ,хм, минимизирующее невязку системы уравнений.

В функции Minerr реализованы те же самые алгоритмы, что и в функции Find, иным является только условие завершения работы численного метода.

Пример использования функции Minerr показан ниже. Как видно, достаточно заменить в вычислительном блоке имя функции на Minerr, чтобы вместо точного (с точностью до TOL) получить приближенное решение уравнения, заданного после ключевого слова Given.

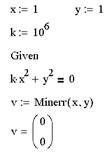
Пример демонстрирует приближенное решение уравнения kx²+y²=0, которое при любом значении коэффициента k имеет единственный точный корень (х=0,у=0).