Определенный интеграл

 

Понятие определенного интеграла.

 

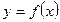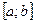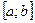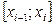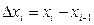Рассмотрим функцию определенную и непрерывную на некотором отрезке числовой прямой. Разобьем на n отрезков длины точками 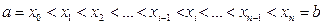. На каждом i-том отрезке берем произвольную точку 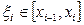. Вычисляем значение функции 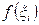в каждой из этих точек и умножаем его на длину соответствующего отрезка . После чего суммируем по всем отрезкам .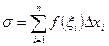

Полученное выражение называют интегральной суммой. Понятие интегральной суммы играет определяющую роль в определении всех интегралов.

Если предел интегральной суммы при стремлении к нулю максимальной длины не зависит ни от способа разбиения отрезка 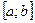на промежутки 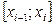, ни от способа выбора точек 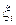в каждом из этих промежутков, то он называется определенным интегралом от функции 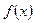в пределах от а до b и обозначается: .

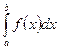Свойства определенного интеграла.

 

I.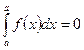

II.

III.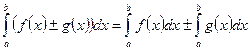

IV.

V.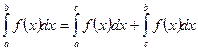

VI. Если 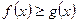для всех 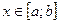, то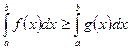

VII. 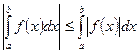, если a<b.

VIII. Теорема о среднем. Если f(x) непрерывна на 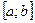, то существует точка , такая что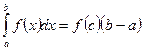

 

Формула Ньютона-Лейбница

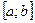Пусть непрерывна на и переменная . Тогда совокупность всех первообразных для этой функции можно выразить формулой 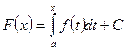. Легко видеть, что . Откуда, заменив переменную интегрирования снова на х, получим формулу Ньютона –Лейбница:

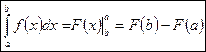
Для того чтобы вычислить определенный интеграл, прежде всего вычисляется одна из первообразных F(x), затем вычисляется значение этой функции в точке b и вычитается её значение в точке а.

Пример.

Вычислить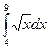

.

*Вычислить интегралы.

1)

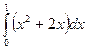
2)

3)

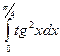
4)

5)

6)

7)

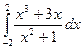
*Вычислить интегралы, используя подходящие замены переменной.

a)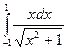

b)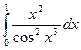

c)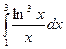

d)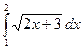

e)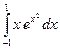

f)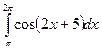

g)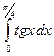

h)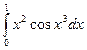

i)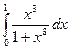

*Вычислить, используя интегрирование по частям.

1.

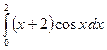
2.

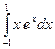
3.

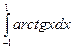
4.

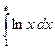
5.

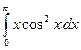
Часть плоскости, ограниченная кривой у=f(x) , осью Ох и прямыми х=a, х=b называется криволинейной трапецией.

 

 

Площадь криволинейной трапеции вычисляется при помощи определенного интеграла.

 

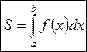
В случае, когда криволинейная трапеция, ограниченная кривой у=f(x) , осью Ох и прямыми х=a, х=b, лежит под осью Ох, площадь находится по формуле:

 

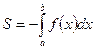
Если фигура, ограниченная кривой у=f(x) , осью Ох и прямыми х=a, х=b, расположена по обе стороны от оси Ох, то:

 

 

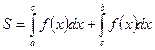
Пусть, наконец, фигура S ограничена двумя пересекающимися прямыми кривыми , где 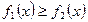и прямыми х=a, х=b,тогда площадь находится по формуле:

 

 

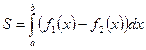
*Вычислить площади фигур, ограниченных указанными линиями.

1)

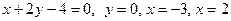
2)

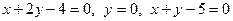
3)

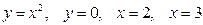
4)

5)

6)

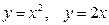
7)

8)

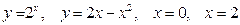
9)

10)

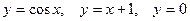
11) 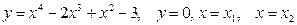, где 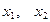- точки в которых функция, задающая первую линию, имеет максимум.