Теорема 2. Для того чтобы функция являлась решением уравнения (2), необходимо и достаточно, чтобы число являлось корнем уравнения
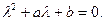 (4)
(4)
Доказательство. Очевидно, что для указанной функции 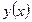 будем иметь
будем иметь 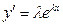 и
и 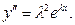 Но тогда условие «
Но тогда условие «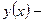 решение уравнения (2)» эквивалентно условию «
решение уравнения (2)» эквивалентно условию «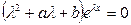 », а это последнее- уравнению (4).
», а это последнее- уравнению (4).
Теорема доказана.
Примечание. Уравнение (4) носит название характеристического уравнения для дифференциального уравнения (2).
Рассмотрим различные случаи разрешимости уравнения (4).
Случай 1. Дискриминант уравнения (4) положителен.
В этом случае уравнение (4) имеет два действительных различных корня, которые мы обозначаем 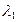 и
и 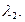 Каждый из этих корней порождает соответствующее решение
Каждый из этих корней порождает соответствующее решение 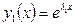 и
и 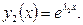 Очевидно, что отношение функций
Очевидно, что отношение функций 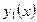 и
и  отлично от постоянной величины, и поэтому общее решение линейного однородного дифференциального уравнения (2) будет иметь вид:
отлично от постоянной величины, и поэтому общее решение линейного однородного дифференциального уравнения (2) будет иметь вид:
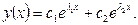
Случай 2. Дискриминант уравнения (4) равен нулю.
Условие равенства нулю дискриминанта уравнения (4) эквивалентно условию 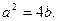 В этом случае уравнение (4) имеет два совпадающих корня:
В этом случае уравнение (4) имеет два совпадающих корня: 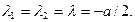
Эти корни порождают одно частное решение 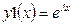 уравнения (2), и для построения общего решения уравнения (2) нам необходимо еще одно решение.
уравнения (2), и для построения общего решения уравнения (2) нам необходимо еще одно решение.
Покажем, что в рассматриваемом случае еще одним решением уравнения (2) будет функция 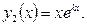
Действительно,

Подставляя эти выражения в уравнение (2), получим
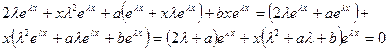
(здесь учтено, что 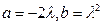 ).
).
Очевидно, что и в этом случае отношение функций 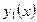 и
и  отлично от постоянной, и поэтому общее решение уравнения (2) будет иметь вид:
отлично от постоянной, и поэтому общее решение уравнения (2) будет иметь вид:
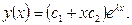 (6)
(6)
Третий случай- случай, когда дискриминант уравнения (3) будет отрицательным, будет рассмотрен нами позже.
Пример 1. Построим общее решение уравнения 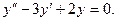
Решение. Характеристическое уравнение (4) для дифференциального уравнения 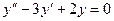 будет иметь вид:
будет иметь вид: 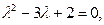 а его корнями будут числа
а его корнями будут числа  и
и  Это означает, что мы имеем случай 1 (случай положительного дискриминанта уравнения (4)), и общее решение рассматриваемого уравнения в соответствии с формулой (5) будет иметь вид:
Это означает, что мы имеем случай 1 (случай положительного дискриминанта уравнения (4)), и общее решение рассматриваемого уравнения в соответствии с формулой (5) будет иметь вид:
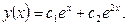
Пример 2. Построим общее решение уравнения 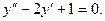
Решение. Для данного дифференциального уравнения характеристическое уравнение (4) будет иметь вид: 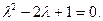 Дискриминант этого уравнения равен нулю, и мы имеем случай 2. Корнями характеристического уравнения (4) будут
Дискриминант этого уравнения равен нулю, и мы имеем случай 2. Корнями характеристического уравнения (4) будут 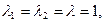 а общее решение, в соответствии с формулой (6), имеет вид
а общее решение, в соответствии с формулой (6), имеет вид 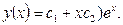
Перейдем теперь к рассмотрению линейного неоднородного дифференциального уравнения второго порядка(1).
Принципиальное значение в проблеме построения его общего решения имеет следующая теорема.
Теорема 3. Общее решение неоднородного дифференциального уравнения (1) имеет вид:
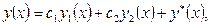 (7)
(7)