Итоги лекции N 7

1. Волновое уравнение для функции Ψ получено в 1926 г. Э. Шредингером и носит его имя - уравнение Шредингера. Для одной частицы, Движущейся во внешнем поле, оно имеет следующий вид (см. (7.1)):

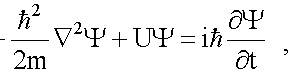
здесь - оператор Лапласа, в декартовой системе координат он имеет следующий вид:

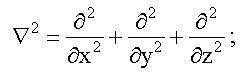
U - потенциальная энергия частицы во внешнем поле, которая может зависеть и от времени;

- мнимая единица.

1. В случае, если внешнее поле, в котором движется частица, не зависит от времени (т.е. U ≠ U(t)), то волновая функция может быть представлена в следующем виде (см. (7.2)):

здесь Е - полная энергия частицы в стационарном состоянии, ψ(x,y,z) - координатная волновая функция.

1. Для координатной волновой функции справедливо уравнение Шредингера для стационарных состояний (см. (7.3)):

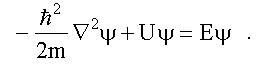
1. Квадраты модулей полной Ψ и координатной y волновых функций совпадают:

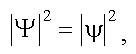
таким образом, |ψ|² в случае стационарных состояний определяет плотность вероятности обнаружения частицы.

1. Для свободой частицы U = 0 и решением уравнения Шредингера является уравнение волны де Бройля (см. (7.13)):

1. Для частицы, движущейся в одномерной бесконечно глубокой потенциальной яме (см. рис. 7.1), из уравнения Шредингера вытекает следующая формула для энергии стационарных состояний (см. (7.21)):

здесь а - размер ямы; m - масса частицы, n - целое число, n = 1,2...

Таким образом, уравнение Шредингера предсказывает квантование энергии микрочастицы, движущейся в ограниченной области.

1. Волновая функция частицы, движущейся в одномерной бесконечно глубокой потенциальной яме имеет следующий вид (см (7.22)):

.