Первая интерполяционная формула Ньютона для равноотстоящих узлов интерполяции

 

Будем искать многочлен Р_n(х) степени п, удовлетворяю­щий условиям (3.2), в виде

Рп(х)= a0 + a1 (x – x0) + a2 (x – x0) (x – x1) + a3 (x – x0) (x – x1) (x – x2) + … + an (x – x0) (x – x1) (x – x2) …(x – xn-1),

(3.15)

где x₀, x₁, … x_n — заданные значения аргумента х, причем x_i — x_i–1 = h = сопst (i=0,1, ... , n), коэффициенты a₀, a₁, .. , a_n нам неизвестны. Будем их определять, исходя из условий (3.2).

Положим в формуле (3.15) х =x₀ . Тогда Р_n(x₀) = a₀ . Однако, в силу условий (3.2), Р_n(x₀) = y₀ . Следовательно, a₀ = y₀ .

Для определения a₁полагаем в (3.15) х = х₁, после чего получим

Р_n(x₁) = a₀ + a₁ (x₁ – x₀).

Учитывая, что Р_n(x₁) = y₁ , a₀ = y₀ , (x₁ – x₀) = h , можем за­писать y₁ = y₀ + a₁h, откуда . Однако y₁ – y₀ = Dy₀ — конечная разность 1-го порядка, следовательно, .

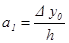Далее, полагая х = х₂, получим

Р_n(x₂) = a₀ + a₁ (x₂ – x₀) + a₂ (x₂ – x₀) (x₂ – x₁).

Так как Р_n(x₂) = y₂ , a₀ = y₀ , 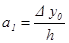, (x₂ – x₀) = 2h, (x₁ – x₀) = h , запишем:

y₂ = y₀ + 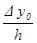2h + a₂2hh;

отсюда

a₂ = .

Но Dy₀ = y₁ – y₂, поэтому

y₂ – y₀ – 2Dy₀ = y₂ – y₀ – 2 (y₁ – y₀) = y₂ – 2 y₁ + y₀ =D²y₀ .

Следовательно,

a₂ = .

 

Аналогичные дальнейшие вычисления (с учетом формулы {3.14), выражающей разности различных порядков через зна­чения функции), позволяют записать остальные коэффициенты:

a₃ = ,… a_k = ,… a_n = .

Подставив найденные выражения коэффициентов в формулу (3.15), получим

Р_п(х) = y₀ + 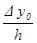(x – x₀) + (x – x₀) (x – x₁) + (x – x₀) (x – x₁) (x – x₂) + … +

+…+ (x – x₀) (x – x₁) (x – x₂)… (x – x_n–1). (3.16)

Это и есть первая интерполяционная формула Ньютона. Ее можно представить в несколько ином виде, более удобном для практического использования. Обозначим

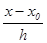= q.

Тогда

= q — 1; 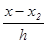= q — 2; …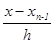= q – n + 1

и формула (3.16) приобретает вид

Р_п(х) = y₀ + qDy₀ + D²y₀ + D³y₀ + … +

+…+ Dny0 .

(3.17)

Формулу (3.17) целесообразно использовать для интерпо­лирования (экстраполирования) функции y=f(x) в окрест­ности начального значения x₀, где qмало по абсолютной ве­личине.

Если в формуле (3.17) принять п= 1, получим формулу линейного интерполирования:

Р₁(х) = y₀ + qDy₀ .

При n = 2 будем иметь формулу параболического, или квад­ратичного, интерполирования:

Р₂(х) = y₀ + qDy₀ + D²y₀ .

При применении первой интерполяционной формулы Ньюто­на удобно пользоваться горизонтальной таблицей конечных раз­ностей, так как тогда нужные значения разностей функции находятся в соответствующей горизонтальной строке таблицы.

Степень п многочлена Р_n(х) на практике желательно вы­бирать так, чтобы конечные разности Dⁿy_i были практически постоянными. За начальное значение x₀ можно принимать лю­бое табличное значение аргумента х.