Тема 10. Аксиоматические начала математики
Изучив данную тему, студент должен знать:
1. Понятие множества, подмножества. Обозначения и изображения множеств. Способы задания множеств.
2. Операции над множествами и свойства операций. Степень множества, формулы числа подмножеств.
3. Основные свойства множеств. Ограниченные и неограниченные множества. Максимум и минимум множества. Грани множества.
4. Основные числовые множества.
5. Определение функции. Области определения и значений функции. Способы задания функции.
6. Основные свойства функций. Возрастание и убывание функции.
Периодическую функцию.
7. Основные элементарные функции.
Уметь:
8. Выполнять операции над множествами и подмножествами.
9. Анализировать элементарные функции и их композиции.
10. Строить и анализировать графики функций.
Решение задач по теории множеств, доказательство формул удобно проводить, пользуясь не только определениями и объектным представлением
о множестве, но и с помощью диаграмм Эйлера. Рассмотрим примеры решения ряда типовых задач.
1. Определить множество А решений уравнения х2 – 25 = 0.
x2 – 25 = 0 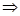 х2 = 25
х2 = 25 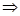 х1 = –5; х2 = 5.
х1 = –5; х2 = 5.
Отсюда: А={x | x2 – 25 = 0}={–5; 5}.
2. Определить множество В решений неравенства 2х + 9 ³ 0.
2х + 9 ³ 0 Þ 2x ³ – 9 Þ x ³ – 4,5.
Отсюда: В={x | 2х+9 ³ 0}={х | x ³ – 4,5}=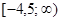 .
.
3. Заданы множества  и
и 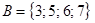 . Определить результаты операций
. Определить результаты операций 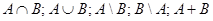 .
.
Изобразим эти множества диаграммами Эйлера и решим задачу:

|



4. Определить результаты тех же операций, если 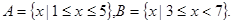
Кружками в этом рисунке обозначим точки, которые являются концами нестрогого неравенства, крестиком – строгого неравенства.
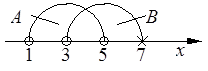
|

5. Определить все подмножества множества А={0; 1; 3}.
Несобственные: Æ и А; одноэлементные: {0}, {1}, {3}; двухэлементные: {0; 1}, {0; 3}, {1; 3}.
Следовательно, степень множества Р(А), т.е. множество всех подмножеств, имеет вид Р(А)={Æ; {0}; {1}; {3}; {0; 1}; {0; 3}; {1; 3}; {0; 1; 3}}.
Для проверки используем теорему: если множество А состоит из n элементов, то число всех его подмножеств равно 2n.
Для нашего примера n=3, следовательно, число подмножеств 23=8, что совпадает с числом объектов в Р(А).
(Для оценивания множеств удобно использовать дополнительные
характеристики. Пусть А – произвольное, но не пустое множество. Число m = max A называется максимумом множества А, если mÎA и
любые другие элементы множества не превосходят этого числа: ai £ m. Аналогично определяется и минимум множества l = min A.
Множество А называется ограниченным сверху, если существует
число k такое, что для всех элементов множества справедливо ai £ k. Это число назовем верхней гранью множества А. Минимально возможное значение k называется точной верхней гранью множества А и обозначается
k = sup A (supremum A).
Множество А называется ограниченным снизу, если существует число p такое, что для всех элементов множества справедливо ai ³ p. Это число назовем нижней гранью множества А. Максимально возможное значение
р называется точной нижней гранью множества А и обозначается p = inf A (infimum A)).
6. Оценить множество А={2; 6; 1; 8}.
В этом множестве легко найти: max A=8; min A=1; sup A=8;
inf A=1.
7. Оценить множество N={1; 2; 3;…}, т.е. натуральный ряд.
Здесь min N=1; max N – не существует; sup N – не существует; inf N=1.
8. Оценить множество А={х| 2 £ x < 5}.
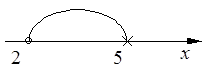
|
Из рисунка следует: min А=2; max A – не существует, так как 5ÏА; sup A=5;
inf A=2.
9. Оценить множество А={х | 3< x < ¥}.

|
Здесь min A – не существует, так как 3ÏА; max A – не существует; inf A=3; sup A – не существует.
Функция – основной описатель различных процессов. Рассмотрим ряд примеров, раскрывающих важные стороны этого базового понятия.
10. Найти область определения (ОДЗ) функции 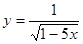 .
.
На множестве R следует выполнить условие:
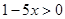 , т.е.
, т.е. 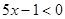 или х < 0,2.
или х < 0,2.
Отсюда: 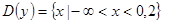 .
.
11. Найти ОДЗ функции 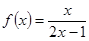 .
.
Так как на ноль делить нельзя, то следует выполнить условие 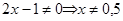 .
.
Отсюда: 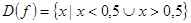 .
.
12. Исследовать на четность функцию  .
.
Положим х1 = 2, х2 = –2. Тогда 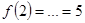 и
и . Так как корреляции типов
. Так как корреляции типов  или
или 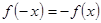 не устанавливаются, следовательно, заданная функция – общего вида.
не устанавливаются, следовательно, заданная функция – общего вида.
13. Исследовать на четность функцию 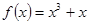 .
.
Принимая те же значения, что и в примере 12, имеем:
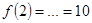 и
и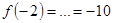 .
.
Так как 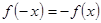 , то заданная функция – нечетная.
, то заданная функция – нечетная.
14. Представить сложную функцию  системой.
системой.
Решение:  .
.
15. Представить сложную функцию 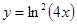 системой.
системой.
Решение:  .
.
С целью более глубокого изучения темы выполните следующие задания.
Задание 10.1. Найти (A È B) Ç С , если A={x | –p1 £ x < p2}; B={x | 0 £ x < p1} и C={x | –p2 £ x <p3}.
Задание 10.2. Оценить множество 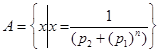 , где nÎN.
, где nÎN.
Задание 10.3. Оценить множество A={x | –p1 < x £ p3}.
Задание 10.4. Оценить множество С=АÇВ, если А={x| x > –p1}
и B={x| –2´p1 £ x < p2}.
Задание 10.5. Найти ОДЗ функции 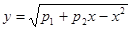 .
.
Задание 10.6. Исследовать на четность функцию: 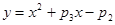 .
.
Задание 10.7. Исследовать на четность функцию:  .
.
Задание 10.8. Построить по точкам график функции