Тема 13. Элементы теории вероятности

Изучив данную тему, студент должен знать:

1. Случайные события и их классификацию

2. Классическое и статистическое определение вероятности.

3. Теоремы сложения и умножения вероятностей.

4. Формулу полной вероятности.

5. Формулу Байеса.

6. Случайные величины и их виды.

7. Закон распределения случайной величины.

8. Распределения: Бернулли, Пуассона, геометрическое.

9. Математическое ожидание случайной величины и его свойства.

10. Дисперсию и ее свойства.

11. Стандарт случайной величины.

Уметь:

12. Решать задачи по определению вероятностей.

13. Вычислять математическое ожидание и дисперсию случайных величин.

14. Практически использовать распределения случайных величин.

Рассмотрим ряд примеров, иллюстрирующих вычисление вероятностей событий и анализ дискретных случайных величин.

1. Брошены два игральных кубика. Найти вероятность того, что сумма очков на выпавших гранях равна пяти, а произведение – четырем.

Каждый кубик при бросании дает одно из чисел 1, 2, 3, 4, 5, 6. Так как оба кубика бросаются независимо, то по теореме умножения общее число исходов: 6 · 6 = 36.

Ясно, что удовлетворить условию задачи возможно только двумя
сочетаниями очков: 1, 4 или 4, 1. То есть только два исхода благоприятствуют условию задачи. Следовательно, по определению вероятности:

2. В коробке имеется 15 шаров, из которых 10 – окрашены, а 5 – прозрачные. Извлекаем, не глядя, три шара. Какова вероятность того, что все они будут окрашены?

Общее число исходов при извлечении шаров:

Благоприятных исходов того, что все шары окрашены:

Следовательно, .

3. В библиотеке на стеллаже расставлено 15 учебников по математике, причем только 5 из них пригодны для студентов юридического факультета. Студент наудачу выбирает 3 учебника. Какова вероятность того, что хотя бы один из учебников – тот, что нужен?

Всего три учебника из 15 можно выбрать:

способами.

Ненужные учебники при этом (из 10 шт.) могут быть выбраны:

способами.

Следовательно, вероятность того, что все учебники непригодны:

Поскольку события А – «хотя бы один учебник пригоден» и – «все три учебника непригодны» противоположны и составляют полную группу, то:

Следовательно, .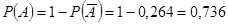

4. Два стрелка одновременно стреляют по мишени. Вероятность попадания для первого стрелка равна 0,7, второго – 0,8. Найти вероятность
того, что в мишень попадет только один стрелок.

Так как два стрелка стреляют одновременно и независимо друг
от друга, то, используя противоположные события «попадание – промах»
и правило умножения вероятностей, получим следующие варианты событий:

– попадают оба стрелка:

;

– попадает первый стрелок и не попадает второй:

;

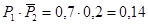– попадает второй и промах у первого:

;

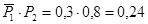– промах обоих стрелков:

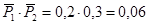Эти события образуют полную группу, так как

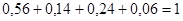Решением задачи, по правилу сложения, будет:

5. Программа экзамена содержит 25 вопросов, из которых студент знает 20. Преподаватель последовательно задает три вопроса. Найти вероятность того, что студент сможет ответить на все вопросы А, В, С.

Вероятность того, что первый вопрос экзаменатора будет из числа
известных студенту, равна

Таким образом, остается 24 вопроса, из которых 19 – известны. Следо-вательно,

Аналогично, вероятность того, что студент ответит и на третий вопрос:

Таким образом, вероятность отличной оценки:

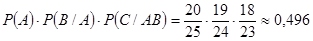6. В мешок, содержащий два шара неизвестного цвета, опущен белый шар. После встряхивания извлечен один шар. Найти вероятность того, что извлеченный шар окажется белым, если равновозможны любые предположения о цвете двух шаров, находившихся в мешке.

Пусть А – событие извлечения белого шара. Построим предположения о первоначальном составе шаров:

В₁– белых шаров нет;

В₂– один белый шар из двух;

В₃– оба шара белые.

Так как гипотезы В₁, В₂ и В₃ по условию равновероятны, то

А теперь промоделируем извлечение:

– если в мешке первоначально не было белых шаров, то:

, так как только одно событие из трех благоприятно;

– в мешке уже был один белый шар, следовательно:

, так как уже два события из трех благоприятны;

– в мешке оба шара были белые:

Искомую вероятность того, что будет извлечен белый шар, найдем
по формуле полной вероятности:

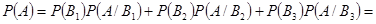
7. Два автомата производят одинаковые детали. Производительность первого автомата в два раза больше производительности второго. Вероятность производства отличной детали у первого автомата равна 0,60,
а у второго 0,84. Наудачу взятая для проверки деталь оказалась отличного качества. Найти вероятность того, что эта деталь произведена первым
автоматом.

Пусть А – событие: деталь отличного качества. Можно сделать две гипотезы:

В₁ – деталь произведена первым автоматом. Тогда , так как этот автомат производит, по условию, деталей в два раза больше второго.

В₂ – деталь изготовлена вторым автоматом, причем .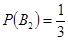

Условные вероятности того, что деталь произведена первым автоматом, по условию: , а вторым – .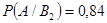

Вероятность того, что наудачу взятая деталь окажется отличного
качества, по формуле полной вероятности:

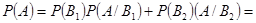
Искомая вероятность того, что взятая деталь изготовлена первым
автоматом, по формуле Байеса:

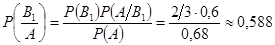8. Дискретная случайная величина X задана законом распределения:

X
p	0,2	0,1	0,4	0,3

Построить многоугольник распределения.

В прямоугольной системе координат по оси x будем откладывать возможные значения x_i, а по оси y – вероятности этих значений. Построим точки 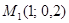; ; 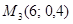и . Соединив эти точки отрезками, получим ответ.

9. Компьютер состоит из трех независимо работающих элементов: системного блока, монитора и клавиатуры. При однократном резком
повышении напряжения вероятность отказа каждого элемента равна 0,1. Исходя из распределения Бернулли составить закон распределения числа отказавших элементов при скачке напряжения в сети.

Возможные значения величины X (число отказов):

x₀ =0 – ни один из элементов не отказал;

x₁ =1 – отказ одного элемента;

x₂ =2 – отказ двух элементов;

x₃ =3 – отказ всех элементов.

Так как, по условию, p = 0,1, то q = 1 – p = 0,9. Используя формулу Бернулли, получим

Контроль: .

Следовательно, искомый закон распределения:

X
p	0,729	0,243	0,027	0,001

10. Произведено 500 выстрелов из винтовки. Вероятность негодного патрона 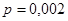. Найти вероятность того, что в серии было ровно три осечки.

Так как n = 500 – велико, а вероятность 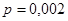– мала и все выстрелы независимы, то имеет место формула Пуассона:

Следовательно, .

11. Найти числовые характеристики случайной величины X, заданной законом распределения:

X	‑5
p	0,4	0,3	0,1	0,2

Математическое ожидание:

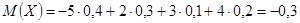Запишем закон распределения X ²:

X ²
p	0,4	0,3	0,1	0,2

Математическое ожидание:

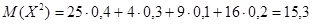Находим дисперсию:

Стандарт .

12. Случайная величина X задана законом распределения

Х
p	0,1	0,3	0,6

Найти начальные и центральные моменты первых трех порядков.

Найдем сначала начальные моменты .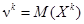

;

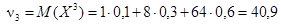Теперь найдем центральные моменты .

;