Обобщение преобразований Фурье. Преобразования Лапласа

Некоторые колебания не могут быть представлены интегралом (1.21), так как для них не существует или не определена спектральная функция. Это происходит потому, что колебание не удовлетворяет условию интегрируемости. Для таких колебаний можно получить преобразования Лапласа, являющиеся обобщением преобразований Фурье.

Умножим некоторое заданное колебание u(t) на e^-ct, где с — положительная константа, выбранная так, чтобы колебание u(t)e^-c удовлетворяло условию абсолютной интегрируемости. Этого можно достигнуть, выбрав с достаточно большим. Тогда спектральная функция выбранного колебания

Обеспечить существование этого интеграла можно, задавая все колебания u(t) так, чтобы u(t) = O при t < 0. В противном случае при отрицательных t множитель e^-ct может привести к расхожде­нию интеграла. При этом нижний предел интегрирования всегда будет равен нулю и

 

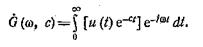
Объединяя степенные множители, получим

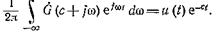
Если произвести обратное преобразование Фурье, то

Умножая обе части на e^ci, объединяя степенные множители под интегралом и заменяя переменную интегрирования w на с + jw, получим

Обозначим в выражениях () и () комплексное число с + jw, через р = с + jw. Полученные после этого соотношения называют парой преобразований Лапласа:

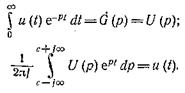(1.29)

Спектральную функцию G(p) = U(p), полученную в результате проделанного обобщения, называют изображением оригинала и(t).

Обратное преобразование осуществляется путем интегрирования в комплексной плоскости р вдоль вертикальной прямой с = const. Из сказанного ясно, что если в выражениях для изображений вместо р подставить jw, то будут получены спектральные функции. Модули спектральных функций убывают с ростом частоты. Это — общая закономерность. Скорость этого убывания зависит от формы импульса. Так, для скачка напряжения модуль спектральной функции убывает пропорционально частоте. Для очень короткого импульса, независимо от его формы, спектральная функция практически постоянна вплоть до частот w< 1/.t Последнее, в частности, означает, что спектр периодической последовательности весьма коротких импульсов содержит гармонические составляющие при весьма высоких частотах. Поэтому короткие импульсы и создают помехи при более высоких частотах.

При осуществлении преобразований Лапласа целесообразно пользоваться теоремами, упрощающими вычисления. Приведем без доказательства важнейшие из них.

Так как преобразования Фурье являются частным случаем преобразований Лапласа, то все теоремы остаются в силе, если вместо изображений писать спектральные функции, а р заменить на jw.